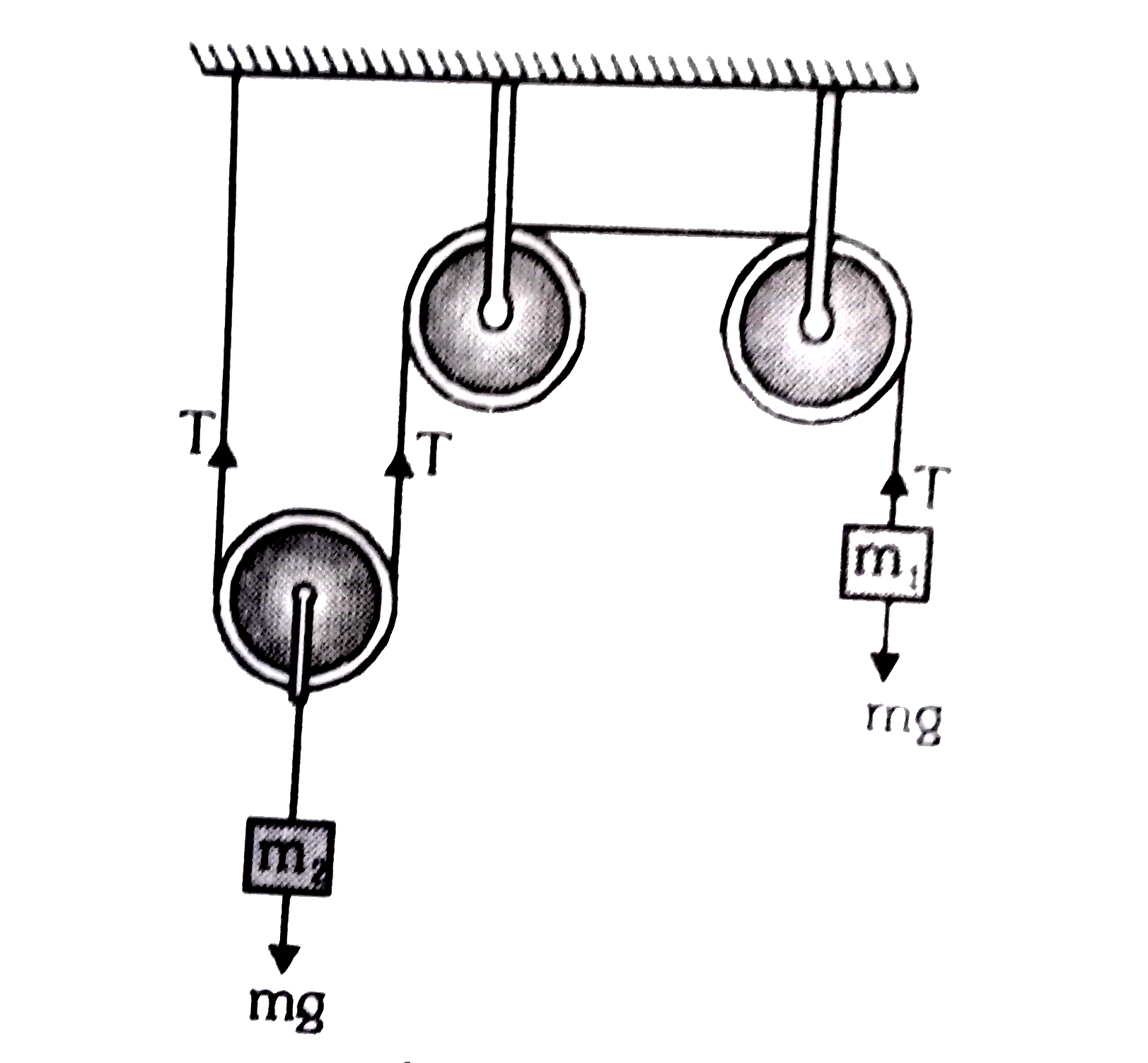
Consider the system of masses and pulleys shown in fig. with massless string and fricitionless pulleys.
(a) Give the necessary relation between masses m1 and m2 such that system is in equilibrium and does not move.
(b) If m1=6kg and m2=8kg, calculate the magnitude and direction of the acceleration of m1.
 Solution in Gujrati
Solution in Gujrati
(a) Applying newton's law m2g−2T=0 (because there is no acceleration) and T−m91)g=0⇒(m2−2m1)g=0⇒m2=2m1
(b) If the upwards acceleration of m1 is a, then acceleration of m2 is a/2 downwards For mass m2:m2g−2T=m2(a2)⇒2m2g−4T=m2a
For mass m1:T−m1g=m1a⇒a=2m2−4m1m2+4m1g=2(8−12)8+24g=−g4
Negative sign shows that acceleration is oppposite to considered direction i.e. it is downwards for m1 and upwards for m2.
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBOOK - ALLEN CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - SWOE
44 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLEN CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-I
52 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLEN CHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)
4 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
25 Videos
Similar Questions
A 2000 kg rocket is set for vertical firing the exhaust speed is 400 m/s to given an initial upward acceleration of 10m/s2. Find out the amount of gas ejected per second to supply the needed thrust (g=10m/s2)
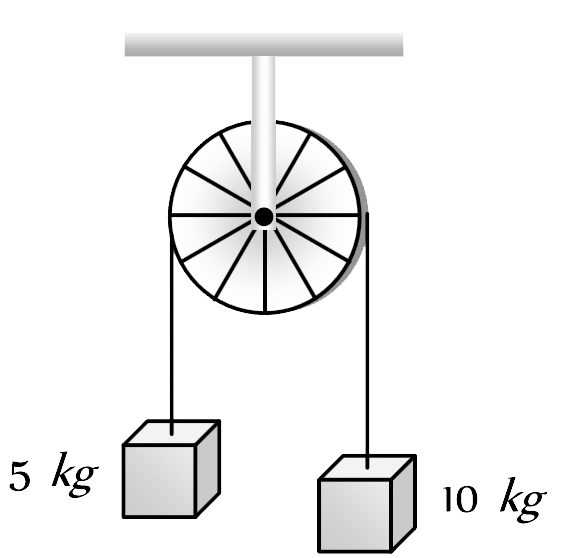
View SolutionUSS 150) Two masses of 5 kg and 10 kg are connected to a pulley as shown. What will be the acceleration of the system (g= acceleration due to gravity)
View SolutionA piece of wire is bent in the shape of a parabola y=kx2 (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
View SolutionThe frequency of a radar is 780 MHz. After getting reflected from an approaching aeroplane, the apparent frequency is more than the actual frequency by 2.6 kHz. The aeroplane has a speed of
View SolutionIn the arrangement shown in fig. m1=1kg,m2=2kg. Pulleys are massless and strings are light. For what value of M, the mass m1 moves with constant velocity.

View SolutionThree blocks of masses m1,m2 and M are arranged as shown in figure. All the surfaces are fricationless and string is inextensible. Pulleys are light. A constant force F is applied on block of mass m1. Pulleys and string are light. Part of the string connecting both pulleys is vertical and part of the strings connecting pulleys with masses m1 and m2 are horizontal.
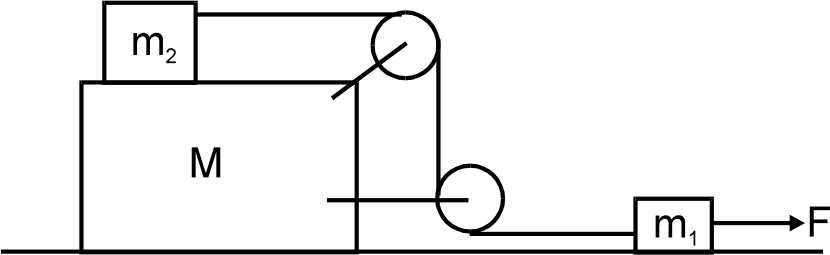
(P)Accleration of mass m1(1)Fm1(Q)Acceleration of massm2(2)Fm1+m2(R)Acceleration of mass M(3)zero(S)Tension in the string(4)m2Fm1+m2
View SolutionIn the system shown in fig., all pulleys are mass less and the string is inextensible and light.
(a) After the system is released, find the acceleration of mass m1
(b) If m1=1kg,m2=2kgandm3=3kg then what must be value of mass m4 so that it accelerates downwards?
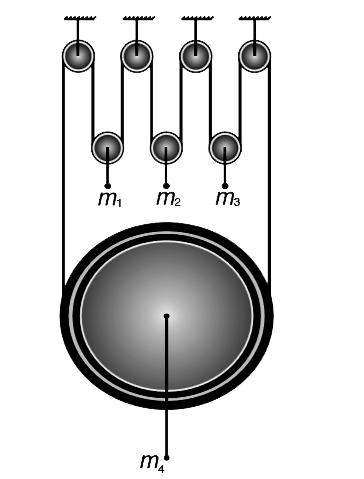
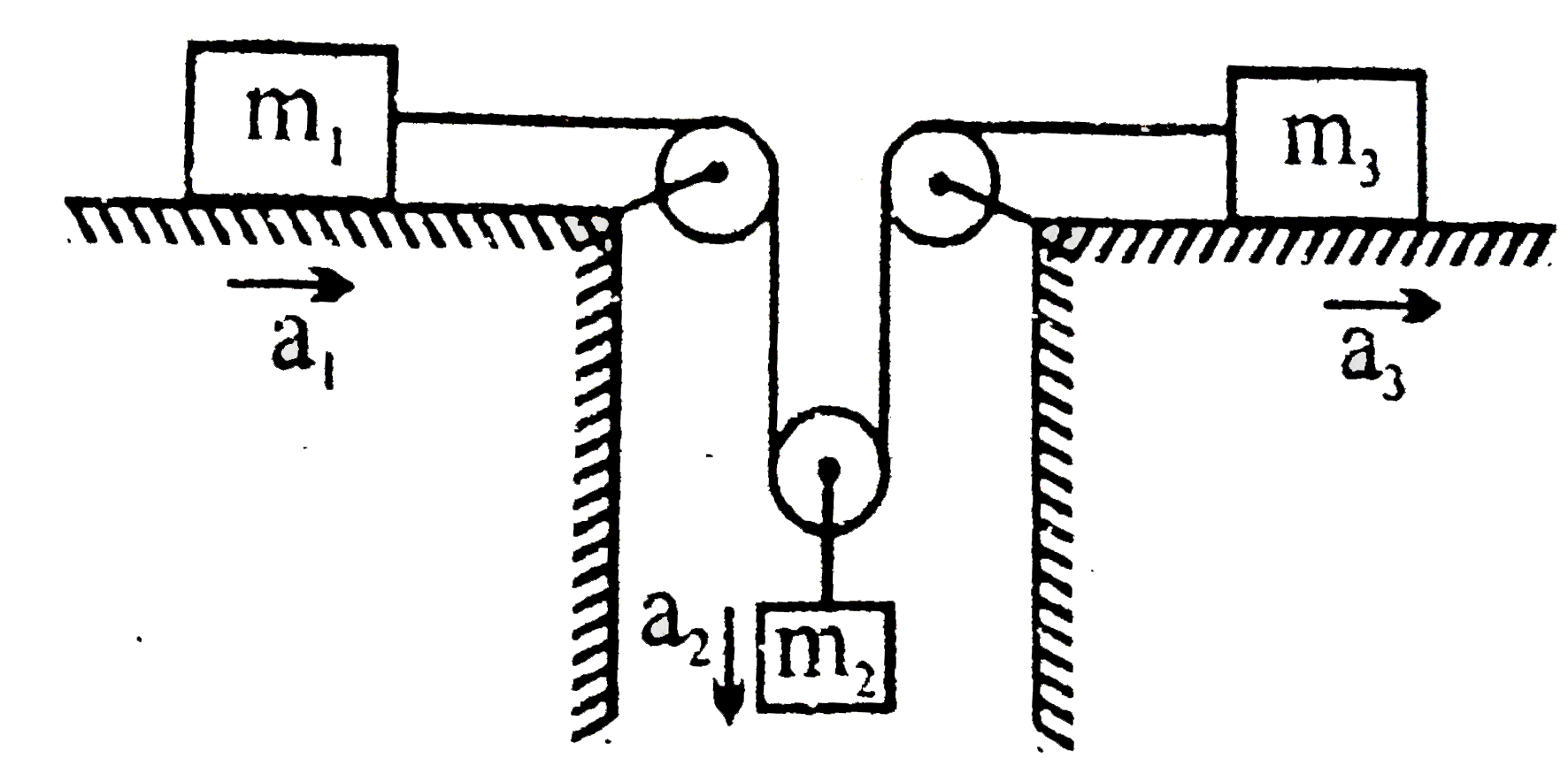
View SolutionIn the pulley system shown here, find the relationship between acceleration of m1,m2 and m3
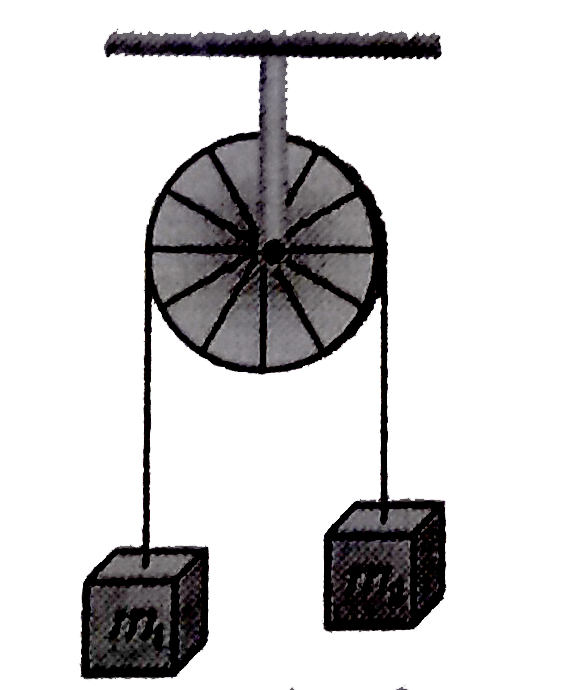
View SolutionTwo masses m1 and m2 are attached to a string which passes over a frictionless smooth pulley. When m1=10kg,m2=6kg, the acceleration of masses is
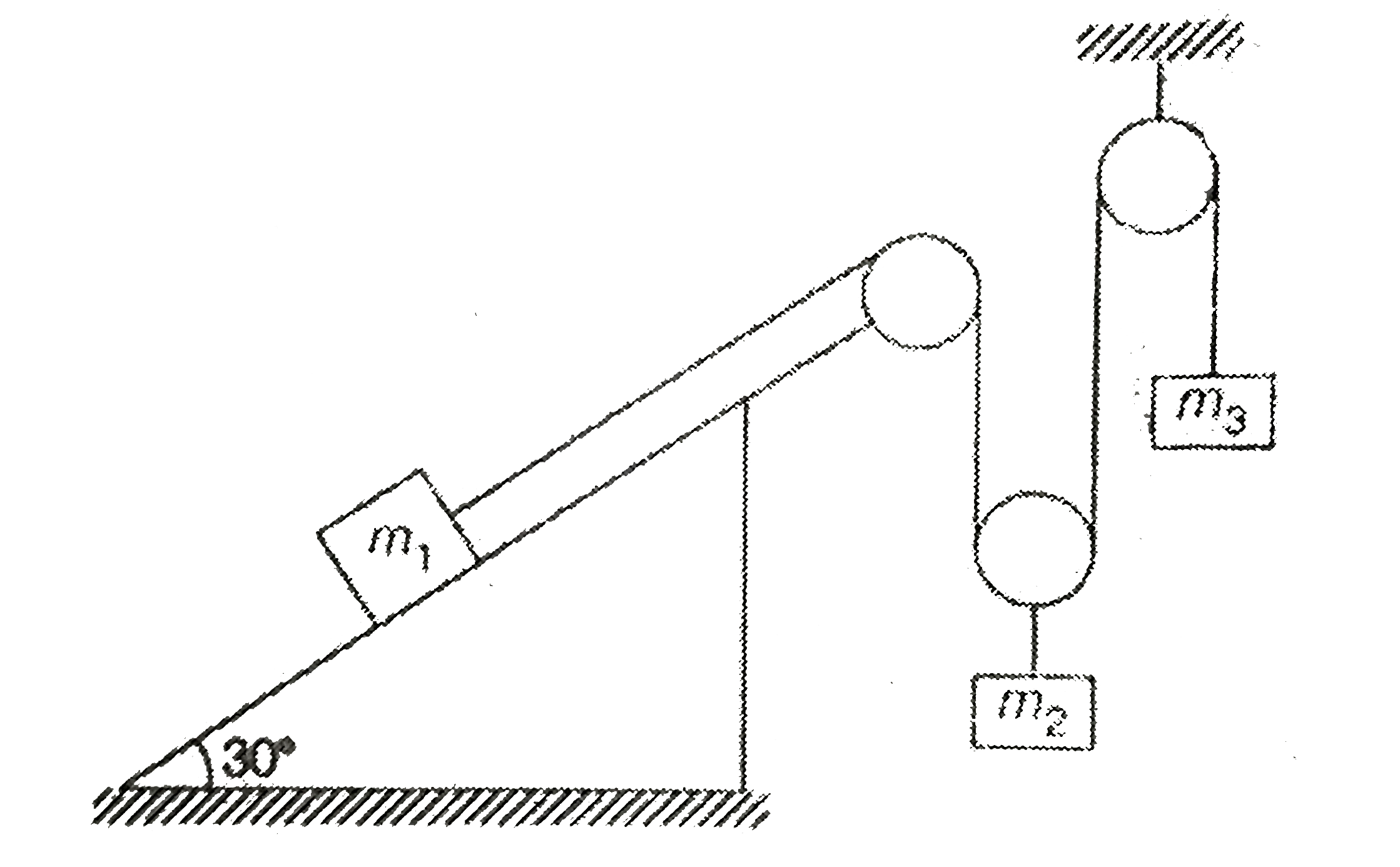
View SolutionA system of masses and pulleys is arranged in a vertical plane as shown in Figure 5.24 her. If mA:mB:mC=3:2:1. Find their accelerations.
View SolutionA situation is shown in figure-2.15, Find the acceleration of masses m_(1) abd m_(2) mass of pulley is m_(P) . Consider the string going over the pulley is massless and frictionless.
View SolutionAll surfaces shown in figure are smooth. For what ratio m1:m2:m2:m3, system is in equilibrium. All pulleys and strings are massless.
View SolutionIn the system shown in fig the pulley is frictionless and the string massless if m_(1)=m_(2) thrust on the pulley will be:
View SolutionTwo masses m1 and m2 are connected to the ends of a massless string that passes over a pulley fixed at the top of a double incline as shown. Assuming m1>m2 acceleration of the system is:

View SolutionConsider a system of masses M_(1) and M_(2)(M_(1) gt M_(2)) connected by a massless string in fig the system is pulled by a force F from the side of mass M_(1) and in fig (b) the system is pulled by the same force F from the side of mass M_(2) then:
View SolutionTwo masses m1 and m2(m2>m1) are hanging vertically over frictionless pulley. The acceleration of the two masses is :

View Solution
