If the momenta of two particles of a system are given by →p1=2ˆi−ˆj+3ˆk and →p2=−ˆi+2ˆj−2ˆk then calculate the angle made by the direction of motion of the system with positive x-axis. Solution in Gujrati
For system →p−→p1+→p2=(2ˆi−ˆj+3ˆk)+(−ˆi+2ˆj−2ˆk)=ˆi+ˆj+ˆk
Let angle made by x-axis be α then cosα=1√3⇒α=cos−1(1√3)
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBOOK - ALLEN CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-I
52 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLEN CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-II
112 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLEN CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLEN CHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)
4 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
25 Videos
Similar Questions
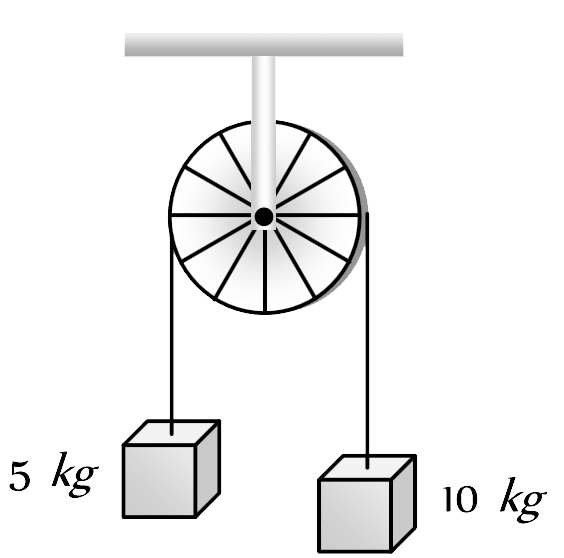
USS 150) Two masses of 5 kg and 10 kg are connected to a pulley as shown. What will be the acceleration of the system (g= acceleration due to gravity)
View SolutionA particle is in straight line motion with uniform velocity A force is not required
View SolutionAssertion: The driver in a vechicle moving with a constant speed on a straight road is in a non-inertial frame of referance.
Reason: A reference frame in which Newton's laws of motion are applicable is non-inertial.
View SolutionA piece of wire is bent in the shape of a parabola y=kx2 (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
View SolutionThe frequency of a radar is 780 MHz. After getting reflected from an approaching aeroplane, the apparent frequency is more than the actual frequency by 2.6 kHz. The aeroplane has a speed of
View SolutionConstant forces →p=2ˆi−5ˆj+6ˆkand→Q=−ˆi+2ˆj−ˆk act on a particle. Determine the work done when the particle is displaced form a point A with position vector 4ˆi−3ˆj+2ˆk to point B with position vector 6ˆi+ˆj−3ˆk.
View SolutionAssertion:- If dipole (→P1) is moved along the line normal to the axis (dotted line shown) of another dipole (→p2), their interaction energy does not chagne.

Reason:- Electric field of →p2 at the position of →p1 is normal to →p1.
View Solutionरेखाओ →r=(ˆi−2ˆj+3ˆk)+λ(ˆi−ˆj+3ˆk) तथा →r=(4ˆi−ˆj)+μ(2ˆi−ˆj+2ˆk) के मध्य कोण ज्ञात कीजिए!
View Solutionएक कण बिन्दु A पर है , इस पर तीन बल →P1=ˆi−ˆj+ˆk , तथा
→P2=−ˆi+2ˆj−ˆkतथा→P3=ˆi−ˆk कार्य कर रहे है | यदि यह कण बिन्दु A से बिन्दु B तक विस्थापित होता है , तो कुल किया गया कार्य ज्ञात कीजिए जबकि A तथा बी के स्थिति सदिश →i−3ˆj−2ˆk तथा
6ˆi+ˆj−3ˆk है | बल →P1 का आघूर्ण बिन्दु कि परितः ज्ञात कीजिए |
View Solutionउस त्रिभुज का क्षेत्रफल ज्ञात करें जिसके शीर्षों के स्थिति सदिश ˆi+ˆj+2ˆk,2ˆi+2ˆj=3ˆk तथा 3ˆi−ˆj−ˆk हैं |
View SolutionThe lines ¯r=ˆi+2ˆj+3ˆk+λ(ˆi+2ˆj+3ˆk)and¯r=−2ˆj+ˆk+λ(2ˆi+2ˆj−2ˆk) are
View Solutionˆi−ˆj+3ˆk,2ˆk+ˆj−2ˆk और ˆi+2ˆj−2ˆk के परिणमी की दिशा में एक एकाक सदिश ज्ञात कीजिए |
View SolutionThe angle beween the lines ˆr=(2ˆi−3ˆj+ˆk)+λ(ˆi+4ˆj+3ˆk)andˆr=(ˆi−ˆj+2ˆk)+μ(ˆi+2ˆj−3ˆk) is
View Solutionदो बल →P1=2ˆi+5ˆj+6ˆk तथा →P2=−ˆi−2ˆj−ˆk एक कण पर क्रिया करके, कण को बिन्दु A (4,-3,-2) से बिन्दु B (6,1,-3) तक विस्थापित कर देते हैं। बलों द्वारा किया गया कार्य ज्ञात कीजिए।
View SolutionFind the angle between the lines →r=ˆi−ˆj+ˆk+λ(2ˆi−2ˆj+ˆk) and →r=2ˆi−ˆj+2ˆk+μ(ˆi+ˆj+2ˆk).
View SolutionIf the sides of an angle are given by vectors →a=ˆi−2ˆj+2ˆkand→b=2ˆi+ˆj+2ˆk, then find the internal bisector of the angle.
View Solution
