A lift can move upward or downward. A light inextensible string fixed from ceiling of lift when a frictionless pulley and tensions in string T1. Two masses of m1andm2 are connected with inextensible light string and tension in this string T2 as shown in figure. Read the questionbs carefully and answer
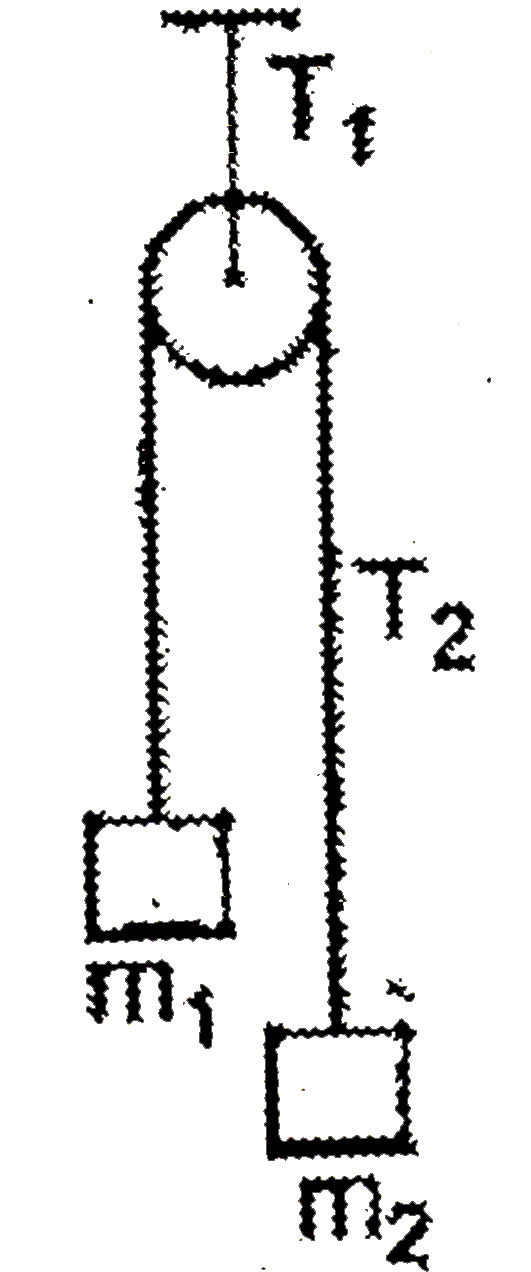
If m1=m2andm1 is moving at a certain instant with velocity v upward with respect to lift and the lift is moving in upward direction with constant acceleration (a<g) then speed of m1 with respect to lift :Solution in Gujrati
T1:T2:T3::1:1:1
T1:T2:T3::6:5:3
T1:T2:T3::3:5:5
T1:T2:T3::6:5:6
The correct Answer is:B
T1mg=m×2∴T1=m×12
T2=mgT2=m×10
mg−T3=m×4T3=m×16
T1:T2:T3=6:5:3
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBOOK - ALLEN CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLEN CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-I
52 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLEN CHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)
4 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
25 Videos
Similar Questions
Assertion: The driver in a vechicle moving with a constant speed on a straight road is in a non-inertial frame of referance.
Reason: A reference frame in which Newton's laws of motion are applicable is non-inertial.
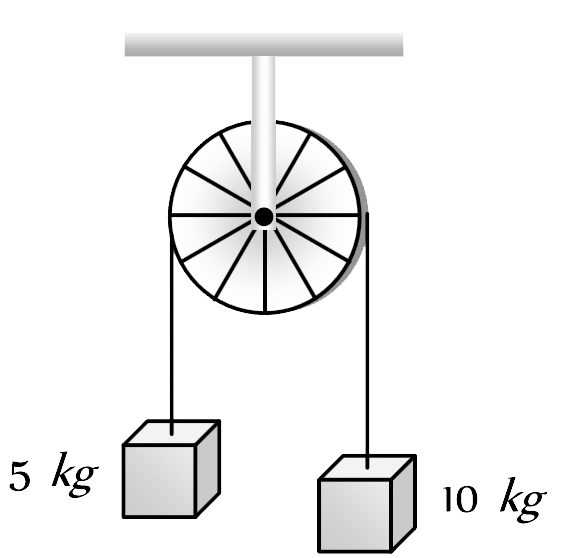
View SolutionUSS 150) Two masses of 5 kg and 10 kg are connected to a pulley as shown. What will be the acceleration of the system (g= acceleration due to gravity)
View SolutionA piece of wire is bent in the shape of a parabola y=kx2 (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
View SolutionThe frequency of a radar is 780 MHz. After getting reflected from an approaching aeroplane, the apparent frequency is more than the actual frequency by 2.6 kHz. The aeroplane has a speed of
View SolutionThree blocks of masses m1,m2 and M are arranged as shown in figure. All the surfaces are fricationless and string is inextensible. Pulleys are light. A constant force F is applied on block of mass m1. Pulleys and string are light. Part of the string connecting both pulleys is vertical and part of the strings connecting pulleys with masses m1 and m2 are horizontal.
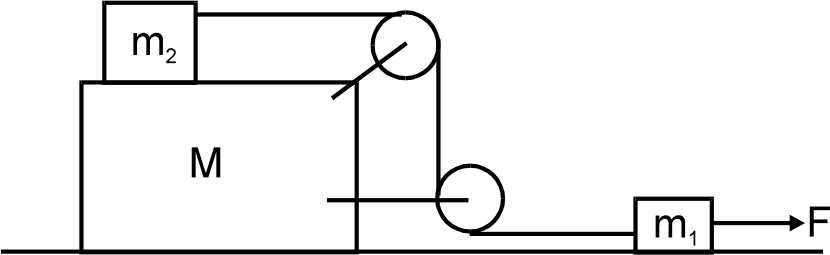
(P)Accleration of mass m1(1)Fm1(Q)Acceleration of massm2(2)Fm1+m2(R)Acceleration of mass M(3)zero(S)Tension in the string(4)m2Fm1+m2
View SolutionTwo masses m_(1) and m_(2) are connected by light inextensible string passing over a smooth pulley P . If the pulley moves vertically upwards with an acceleration equal to g then .
View SolutionA lift can move upward or downward. A light inextensible string fixed from ceiling of lift when a frictionless pulley and tensions in string T_(1) . Two masses of m_(1) and m_(2) are connected with inextensible light string and tension in this string T_(2) as shown in figure. Read the questionbs carefully and answer If m_(1)+m_(2)=m and lift is moving with constant velocity then value of T_(1) :
View SolutionA lift can move upward or downward. A light inextensible string fixed from ceiling of lift when a frictionless pulley and tensions in string T1. Two masses of m1andm2 are connected with inextensible light string and tension in this string T2 as shown in figure. Read the questionbs carefully and answer

If m1 is very small as compared to m2 and lift is moving with constant velocity then value of T2 is nearly :
View SolutionFind the acceleration of masses m_(1) and m_(2) connected by an inextensible string, shown in figure-2.13(a). The string and pulley are assumed to be massless and frictionless.
View SolutionTwo bodies of masses m1 and m2 are connected a light string which passes over a frictionless massless pulley. If the pulley is moving upward with uniform acceleration g2, then tension in the string will be
View SolutionTwo objects A and B of masses m_(A) and m_(B) are attached by strings as shown in fig. If they are given upward acceleration then the rato of tension T_(1) : T_(2) is-
View SolutionA block of mass m_(1)=2 kg is kept on a smooth horizontal table. Another block of mass m_(2)=1 kg is connected to m_(1) by a light inextensible string passing over a smooth pulley as shown in the figure. If the blocks are released, what will be the (a) acceleration of each block (b) tension in the string?
View SolutionConsider the case of two bodies of masses m1andm2 which are connected by light inextensible string passing over a light smooth pulley as shown in the figure. The expression for acceleration of the system and tension of the string are expressed below under different situations:
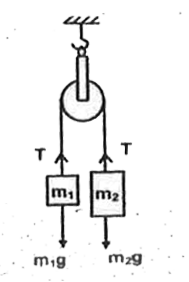
(i) when m1>m2. In this case
a=(m1−m2m1+m2)gandT=(2m1m2m1+m2)g
(ii) when m2>m1. In this case
a=(m2−m1m1+m2)gandT=(2m1m2m1+m2)g
(iii) When m1=m2=m. In this case a=0,T=mg
What is the tension in the string?
View SolutionConsider the case of two bodies of masses m_(1) and m_(2) which are connected by light inextensible string passing over a light smooth pulley as shown in the figure. The expression for acceleration of the system and tension of the string are expressed below under different situations: (i) when m_(1) gt m_(2) . In this case a=((m_(1)-m_(2))/(m_(1)+m_(2)))g and T=((2m_(1)m_(2))/(m_(1)+m_(2)))g (ii) when m_(2) gt m_(1) . In this case a=((m_(2)-m_(1))/(m_(1)+m_(2)))g and T=((2m_(1)m_(2))/(m_(1)+m_(2)))g (iii) When m_(1)=m_(2)=m . In this case a = 0, T = mg If the pulley is pulled upward with acceleration equal to the acceleration due to gravity, what will be the tension in the string?
View SolutionFind the relation between acceleration of the two blocks m_(1) and m_(2) . Assume pulleys are massless and frictionless and the strings are inextensible .
View SolutionShown in the figure is a system of three bodies of mass m_(1), m_(2) & m_(3) connected by a single inextensible light string. If all surfaces in contact are smooth & the pulleys P & Q are light, find the tension in the string.
View Solution
