A massless string passes over a frictionless pulley and carries mass m1 hanging at one end and mass m2 connected by another massless string to mass m3 at other end as shown in figure . Calculate the tension in string joining masses m2and m3.
Let T1 be the tension in the string joining m1andm2 , whileT2 the tension is string joining m2and m3
Let a be acceleration of masses. The resultant force on mass m3 is (m3g−T) downward, therefore , we have
m3g−T2=m3a ....(1)
Resultant force on mass m2 is
(m2g+T2−T1) downward , therefore , we have
m2g+T2−T1=m2a ....(2)
Resultant force on mass m1 is (T1−m1g)upward , therefore , we have
T1−m1g=m1a ....(3)
Adding (1),(2) and (3) , we get , m3g+m2g−m1g=(m3+m2+m1)a
∴acceleration a=(m2+m3−m1)m1+m2+m3g<br>⊂stitut∈gthisvalueofa∈(1),we≥t<br>m_(3)g-T_(2)=m_(3).((m_(2)+m_(3)-m_(1))g)/(m_(1)+m_(2)+m_(3))<br>ThisgivesT_(2)=m_(3)g-(m_(3)(m_(2)+m_(3)-m_(1))g)/(m_(1)+m_(2)+m_(3))<br>:. "Required Tension , " T_(2)=(2m_(1)m_(3)g)/(m_(1)+m_(2)+m_(3))

Similar Questions
Two masses m1 and m2 are connected by a massless string as shown in Fig. Find the value of tension in the string if a force of 200 N is applied on (i) m1 and m2.

View SolutionA string of lenth l fixed at one end carries a mass m at the other end. The strings makes 2πrevs−1 around the axis through the fixed end as shown in the figure, the tension in the string is

View Solution
Knowledge Check
Two masses ,each equal to m ,are arrached to one another by a massless string passing over a smooth pulley the tension in the string is :
AmgB2mgCmg/2DzeroA string of length l fixed at one end carries a mass m at the other end. The strings makes 2πrevs−1 around the axis through the fixed end as shown in the figure, the tension in the string is
 A16 mlB4 mlC8 mlD2 ml
A16 mlB4 mlC8 mlD2 mlA smooth massless string passes over a smooth fixed pulley. Two masses m1 and m2(m1>m2) are tied at the two ends of the string. The masses are allowed to move under gravity starting from rest. The total external force acting on the two masses is
A(m1+m2)gB(m1−m2)2m1+m2gC(m1−m2)gD(m1+m2)2m1−m2g
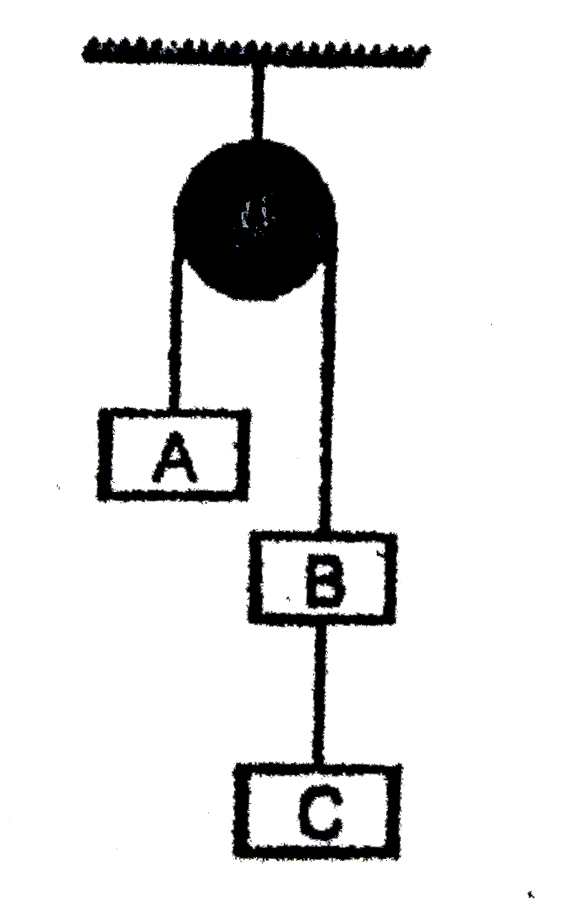
Figure shows three blocks of mass m each hanging on a string passing over a pulley. Calculate the tension in the string connecting A to B and B to C?

View SolutionTwo blocks each of mass m are connected over two light and frictionless pulleys and a fixed wedge by a light string as shown in figure. The tension in the string is :
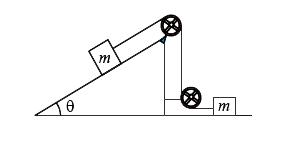
View SolutionTwo blocks each of mass m are connected over two light and frictionless pulleys and a fixed wedge by a light string as shown in figure. The tension in the string is :

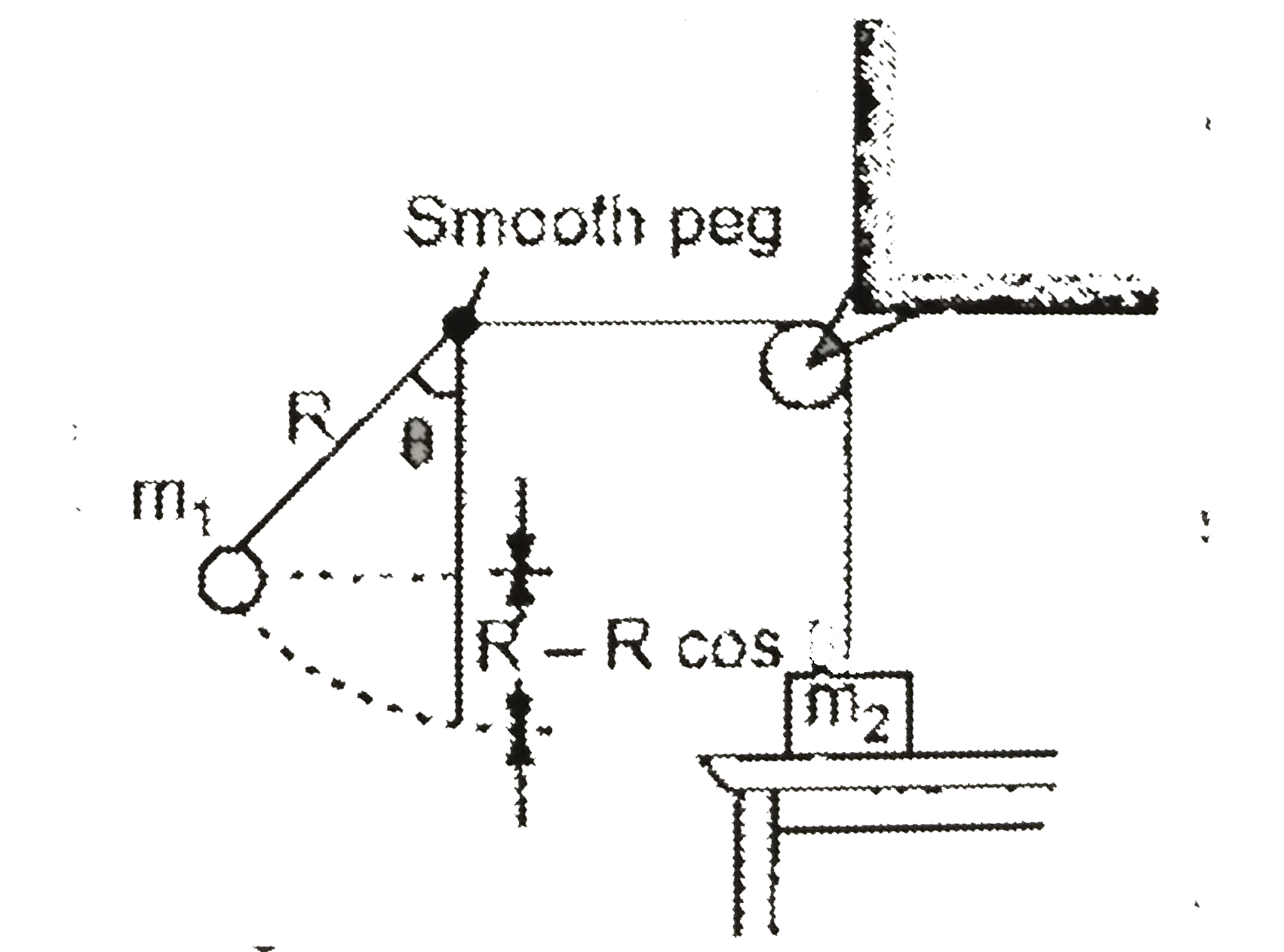
View SolutionTwo blocks are connected by a massless string that passes over a frictionless peg as shown in Fig. 3E.46. One end of the string is attached to a mass m1=3kg i.e. a distance R=1.20m from the peg. The other end of the string is connected to a block of mass m2=6kg resting on a table. From what angle θ, measured from the vertical, must the 3 kg block be released in order to just lift the 6 kg block off the table ?
View SolutionThree blocks A,B and C of mass 10 kg each are hanging on a string passing over a fixed frictionless pulley as shown in figure. The tension in the string connecting blocks B and C is (g=10m/s2)
View Solution
