A car is moving along a straight horizontal road with a speed v0 . If the coefficient of friction between the tyres and the road is μ , the shortest distance in which the car can be stopped is Solution in Gujrati
V202μg
V20μg
(V0μg)2
2V20μg
The correct Answer is:A
O2−V20=2(−μg)×s
s=V202μg
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBOOK - ALLEN CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLEN CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-I
52 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLEN CHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)
4 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
25 Videos
Similar Questions
Assertion: The driver in a vechicle moving with a constant speed on a straight road is in a non-inertial frame of referance.
Reason: A reference frame in which Newton's laws of motion are applicable is non-inertial.
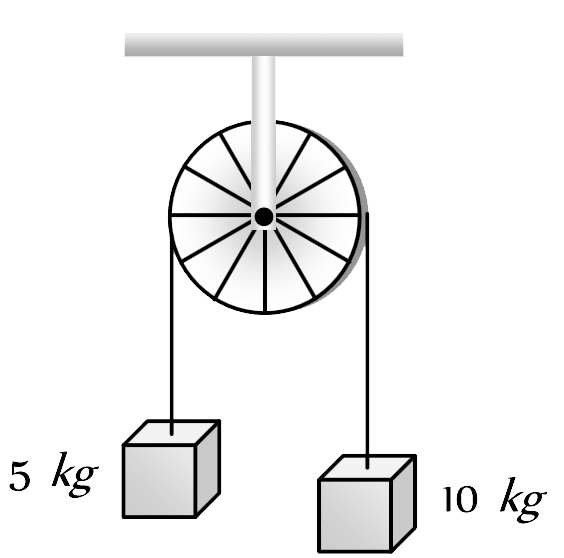
View SolutionUSS 150) Two masses of 5 kg and 10 kg are connected to a pulley as shown. What will be the acceleration of the system (g= acceleration due to gravity)
View SolutionA piece of wire is bent in the shape of a parabola y=kx2 (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
View SolutionThe frequency of a radar is 780 MHz. After getting reflected from an approaching aeroplane, the apparent frequency is more than the actual frequency by 2.6 kHz. The aeroplane has a speed of
View SolutionA car is travelling along a curved road of radius r. If the coefficient of friction between the tyres and the road is mu the car will skid if its speed exceeds .
View SolutionWhat is the minimum stopping distance for a vehicle of mass m moving with speed v along a level road. If the coefficient of friction between the tyres and the road is mu .
View SolutionWhat is the minimum stopping distance for a vehicle of mass m moving with speed v along a level road. If the coefficient of friction between the tyres and the road is mu
View SolutionConsider, a car moving along a straight horizontal road with a speed of 72 km/h. If the coefficient of static friction between the distance in which the car can be stopped is (Take g=10 //s^(2) )
View SolutionConsider a car moving along a straight horizontal road with a speed of 72 km / h . If the coefficient of kinetic friction between the tyres and the road is 0.5, the shortest distance in which the car can be stopped is [g=10ms−2]
View SolutionA car starts rest, on a horizontal circular road of radius R, the tangential acceleration of the car is a. The friction coefficient between the road and the tyre is μ Find the speed at which car will skid and also find the distance after travelling it skids.
View Solutionएक मोटर-कार सीधी क्षैतिज सड़क पर u चाल से चल रही है। यदि सड़क तथा टायरों के बीच स्थैतिक घर्षण गुणांक μs हो, तो वह कम-से-कम दूरी क्या है जिसमे मोटर-कार को रोका जा सके?
View SolutionConsider a car moving along a straight horizontal road with a speed of 72 km/h. If the coefficient of static friction between the tyres and the road is 0.5, the shortest distance in which the car can be stopped is [g=10 ms^(-1)]
View SolutionA car is moving along a straight horizontal road with a speed V. If the coefficient of friction between road and tyres is H, the shortest distance in which the car stops when engine is shut off, is :
View Solutionएक कार सीधी क्षैतिज रोड पर 'v0' वेग से गति कर रही है। यदि रोड तथा कार के टायरों के मध्य घर्षण गुणांक μ हो तो वह न्यूनतम दूरी ज्ञात करो जिसमें कार को ब्रेक लगाकर रोका जा सके।
View SolutionA car starts rest, on a horizontal circular road of radius R, the tangential acceleration of the car is a. The friction coefficient between the road and the tyre is μ Find the speed at which car will skid and also find the distance after travelling it skids.
View SolutionConsider a car moving along a straight horizontal road with a speed of 72 km/h. If the coefficient of static friction between road and tyres is 0.5, the shortest distance in which the car can be stopped is
View Solution
