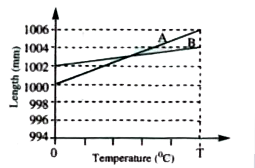
The variation of lengths of two moles rods A and B with change in temperature is shown in figure . The ratio of αaαB is :-
_E01_013_Q01.png) Solution in Gujrati
Solution in Gujrati
32
23
43
34
The correct Answer is:B
l=l0(1+αΔT)⇒l−l0=l0αΔT
⇒l0αAΔTl0αBΔT=104−100106−100=46⇒αAαB=23
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -02
82 Videos
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -03
11 Videos
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - SOME WORKED OUT EXAMPLES
84 Videos
- CURRENT ELECTRICITYBOOK - ALLEN CHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
A triangular plate has two cavities , one square and one rectangular as shown in figure . The plate is heated.
_E01_066_Q01.png)
View SolutionThree liquids A,B and C having same specific heat and mass m , 2m and 3 m have temperature 20∘C,40∘C and 60∘C respectively. Temperature of the mixture when:
Column-IColumn-II(A)A and B are mixed(p)33∘C(B)A and C are mixed(q)52∘C(C)B and C are mixed(r)50∘C(D)A,B and C all three are mixed(s)46∘C(t)None
View SolutionIn an 20 m deep lake, the bottom is at a constant temperature of 4∘C. The air temperature is constant at −10∘C. The thermal conductivity of ice in 4 times that water. Neglecting the expansion of water on freezing, the maximum thickness of ice will be
View SolutionIn the Bohr's model of hy drogen atom, the electron moves around the nucleus in a circular orbit of radius 5×10−11m. Its time period is 1.5×10−16s. The current associated with the electron motion is:-
View SolutionAssertion : The difference in the value of acceleration due to gravity at pole and equator is proportional to square of angular velocity of earth.
Reason : the value of acceleration due to gravity is minimum at the equator and maximum at the pole.
View SolutionThe length of two metallic rods at temperatures theta are L_(A) and L_(B) and their linear coefficient of expansion are alpha_(A) and alpha_(B) respectively. If the difference in their lengths is to remian constant at any temperature then
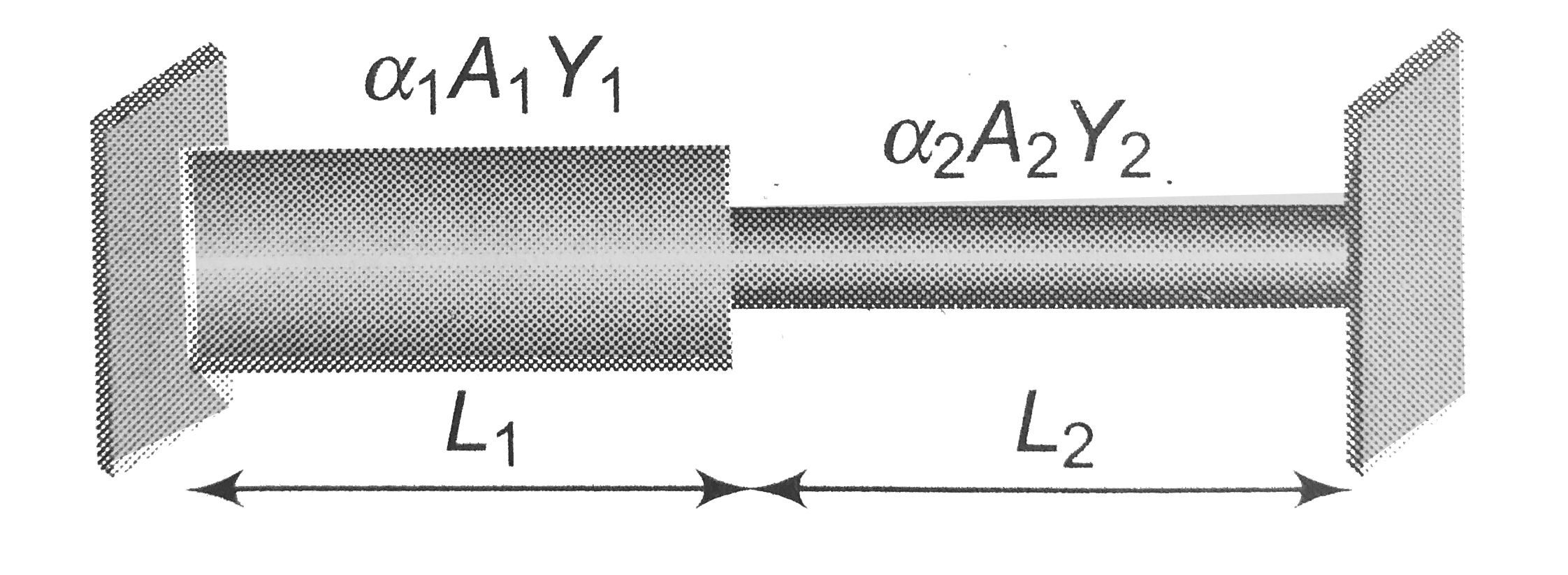
View SolutionTwo rods are joined between fixed supports as shown in the figure. Condition for no change in the length of individual rods with the increase of temperature will be "(" alpha_(1), alpha_(2)= linear expansion coefficient A_(1), A_(2)= Area of rods Y_(1), Y_(2)= Young modulus ")"
View SolutionIf the roots of equation x3+ax2+b=0areα1,α2,and
α3(a,b≠0). Then find the equation whose roots are
α1α2+α2α3α1α2α3,α2α3+α3α1α1α2α3,α1α3+α1α2α1α2α3.
View SolutionA bimetallic is made of two strips A and B having coefficients of linear expansion alpha_(4) and alpha_(B) . If alpha_(A) lt alpha_(B) , then on heating, the strip will
View SolutionTwo rods of length L1 and L2 are made of materials of coefficients of linear expansions α1 an α2 respectively such that L1α1=L2α2. The temperature of the rods is increased by ΔT and correspondingly the change in their respective lengths be ΔL1 and ΔL2
View SolutionIf the roots of equation x3+ax2+b=0areα1,α2,and
α3(a,b≠0). Then find the equation whose roots are
α1α2+α2α3α1α2α3,α2α3+α3α1α1α2α3,α1α3+α1α2α1α2α3.
View SolutionTwo rods of same length made of brass and steel of equal cross-sectional area are joined end to end as shown in figure (a) and supported between two rigid vertical walls. Initially the rods are unstrained. If the temperature of system is raised by ΔT, find the displacement of the junction of the rods. Given that the coefficients of linear expansion and Young.s modulus of brass and steel are αb,αs(αb>αs),ybandys respectively.

View SolutionThe variation of length of two metal rods A and B with change in temperature are shown in fig. The coefficients of linear expansion αA for the metal A and the temperature T will be (Given αa=9×10−6/°C )
View SolutionTwo rods of same length made of brass and steel of equal cross-sectional area are joined end to end as shown in figure ( a) and supported between two rigid vertical walls. Initially the rods are unstrained. If the temperature of system is raised by ΔT, find the displacement of the junction of the rods. Given that the coefficients of linear expansion and Young's modulus of brass and steel are αb,αs(αb>αs),ybandys respectively.

View SolutionTwo rods are joined between fixed supports as shown in the figure. Condition for no change in the length of individual rods with the increase of temperature will be
(α1,α2= linear expansion coefficient
A1,A2= Area of rods
Y1,Y2= Young modulus )
View SolutionThe variation of lengths of two metal rods A and B with change in temperature are as shown in the figure. The ratio of αBαA is (Here αA= Linear coefficient of thermal expansion of rod A3αB= Linear coefficient of thermal expansion of rodB .
'(##CEN_KSR_PHY_JEE_C13_E01_016_Q04##)'
View Solution
