Two rods of same length made of brass and steel of equal cross-sectional area are joined end to end as shown in figure ( a) and supported between two rigid vertical walls. Initially the rods are unstrained. If the temperature of system is raised by ΔT, find the displacement of the junction of the rods. Given that the coefficients of linear expansion and Young's modulus of brass and steel are αb,αs(αb>αs),ybandys respectively.

Here the initial lengths of the two rods are l0 and as αb>αs , we can directly state that the junction of the two rods is displaced toward right. Due to this brass rod is some what expanded but less as compared to free expansion and steel is overall compressed due to the stress developed between the two rods.

Figure (b) shows the final situation of rods at higher temperature Δt. In figure, A is the initial position of junction and B is its final position.
If only brass rod is present, expansion in it due to increase in temperature by ΔT is
Δlb=αbl0ΔT
which is equal to AC in figure b. But finally the rod is expanded by x, thus the elastic compression in the rod due to stress between the two rods is BC, which . is given as BC = αbl0ΔT−x
Thus elastic strain in brass rod is
(Strain)brass=αbl0ΔT−xl0[ As αbl0ΔT is small ]
Similarly if steel rod alone is there, it would have been expanded by Δls=αsl0ΔT
which is equal to AD in figure b. But finally steel rod is compressed hy x, thus the elastic compression in steel rod due to stress between the two rods in BD, which is given as BD = αsl0ΔT + x
Thus elastic strain in steel rod is
(Strain)brass=αbl0ΔT−xl0[ As αbl0ΔT is small ]
As the two rods are in contact, stress developed in the two rods must be equal so,
we have (Stress)brass=(Stress)steel
or yb×(Strain)brass=ys×(Strain)steel
or yb[αblbΔT−xl0]=ys[αsl0ΔT+xl0]
or x = (ybαb−ysαs)l0ΔT(yb+ys)
Similar Questions
Two same length rods of brass and steel of equal cross-sectional area are joined end to end as shown in figure and supported between two rigid vertical walls. Initially the rods are unstrained. If the temperature of system is raised by Δt. Find the displacement of the junction of two rods. Given that the coefficient of linear expansion and young's modulus of brass and steel are aphab.αs(αb>αs),Yb and Ys respectively.
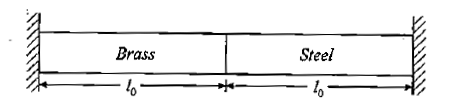
View SolutionTwo rods of equal cross sections area are joined end the end as shown in figure. These are supported between two rigid vertical walls. Initially the rods are unstrained .
_E01_227_Q01.png)
If temperature of system is increased by ΔT then junction will not shift if -
View Solution
Knowledge Check
Two rods of equal cross sections area are joined end the end as shown in figure. These are supported between two rigid vertical walls. Initially the rods are unstrained .
_E01_227_Q01.png)
If temperature of system is increased by ΔT then junction will not shift if -AY1α1=Y2α2BY1α1l1=Y2α2l2Cα1=α2DY2α1l2=Y1α2l2Two rods of equal cross sections area are joined end the end as shown in figure. These are supported between two rigid vertical walls. Initially the rods are unstrained .
_E01_228_Q01.png)
If temperature of system is increased by ΔT then thermal stress developed in first rod-Ais equal to thermal stress developed in second rodBis greater than thermal stress developed in second rodCis less than thermal stress developed in second rodDNone of theseTwo rods of equal cross sections area are joined end the end as shown in figure. These are supported between two rigid vertical walls. Initially the rods are unstrained .
_E01_229_Q01.png)
If temperature of system is increased by ΔT then shifting in junction if junction if Y1α1>Y2α2 is given by -Al1l2(Y1α2−Y2α1)Y1l1+Y2l2Bl1l2(Y1α1−Y2α2)Y1l2+Y2l1Cl1l2(Y1α1−Y2α2)Y1l1+Y2l2DNone of these
Two rods of equal cross sections area are joined end the end as shown in figure. These are supported between two rigid vertical walls. Initially the rods are unstrained .
_E01_228_Q01.png)
If temperature of system is increased by ΔT then thermal stress developed in first rod-
View SolutionTwo rods of equal cross sections area are joined end the end as shown in figure. These are supported between two rigid vertical walls. Initially the rods are unstrained .
_E01_229_Q01.png)
If temperature of system is increased by ΔT then shifting in junction if junction if Y1α1>Y2α2 is given by -
View SolutionTwo steel rods and an aluminum rod of equal length l0 and equal cross section are joined rigidly at their ends as shown in the figure below. All the rods are in a state of zero tension at 0∘C. Find the length of the system when the temperature is raised to θ. Coefficient of linear expansion of aluminum and steel are αaandαs respectively. Young's modulus of aluminum is Ya and of steel is Ys.

View SolutionTwo steel rods and an aluminium rod of equal length l0 and equal cross- section are joined rigidly at their ends as shown in the figure below. All the rods are in a state of zero tension at 0∘C. Find the length of the system when the temperature is raised to θ. Coefficient of linear expansion of aluminium and steel are αa and αs respectively. Young's modulus of aluminium is Ya and of steel is Ys.
View SolutionTwo rods of different materials having differnet lengths and same cross sectional areas are joined end to end in a straight line. The free ends of this compound rod are maintained at different temperatures The temperature gradient in each rod will be .
View Solution
