Graph shows a hypothetical speed distribution for a sample of N gas particle :- (forV>V0,dNdV=0)
_E01_138_Q01.png) Solution in Gujrati
Solution in Gujrati
The value of aV0 is 2N.
The ratio Vavg/V0 is equal to 2/3.
The ratio Vavg/V0 is equal to 1/√2.
Three fourth of the total particle has a speed between 0.5V0 and V0.
The correct Answer is:A, B, C, D
Area under the curves is equal to number of molecules of the gas sample.
Hence N=12aV0⇒aV0=2N
Vavg=1N∞∫0vN(V)dV=1NV0∫0C.(aV0V)dV=23V0
VavgV0=23
V2rms=1N∞∫0V2N(V)dV=1NV0∫0V2.(aV0V)dV=V202
⇒VrmsV0=1√2
Area under the curve from 0.5V0 to V0 is 3/4 of total area
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -03
11 Videos
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - ASSERTION-REASON
40 Videos
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -01
65 Videos
- CURRENT ELECTRICITYBOOK - ALLEN CHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
Three liquids A,B and C having same specific heat and mass m , 2m and 3 m have temperature 20∘C,40∘C and 60∘C respectively. Temperature of the mixture when:
Column-IColumn-II(A)A and B are mixed(p)33∘C(B)A and C are mixed(q)52∘C(C)B and C are mixed(r)50∘C(D)A,B and C all three are mixed(s)46∘C(t)None
View SolutionStatement-1: A real gas behaves as an ideal gas at high temperature and low pressure .
Statement-2: Liquid state of an ideal gas is impossible.
View SolutionOn an X temperature scale, water freezes at −125.0∘X and boils at 375.0∘X. On a Y temperature scale, water freezes at −70.0∘Y and boils at −30.0∘Y. The value of temperature on X-scale equal to the temperature of 50.0∘Y on Y-scale is
View SolutionIn the Bohr's model of hy drogen atom, the electron moves around the nucleus in a circular orbit of radius 5×10−11m. Its time period is 1.5×10−16s. The current associated with the electron motion is:-
View SolutionAssertion : The difference in the value of acceleration due to gravity at pole and equator is proportional to square of angular velocity of earth.
Reason : the value of acceleration due to gravity is minimum at the equator and maximum at the pole.
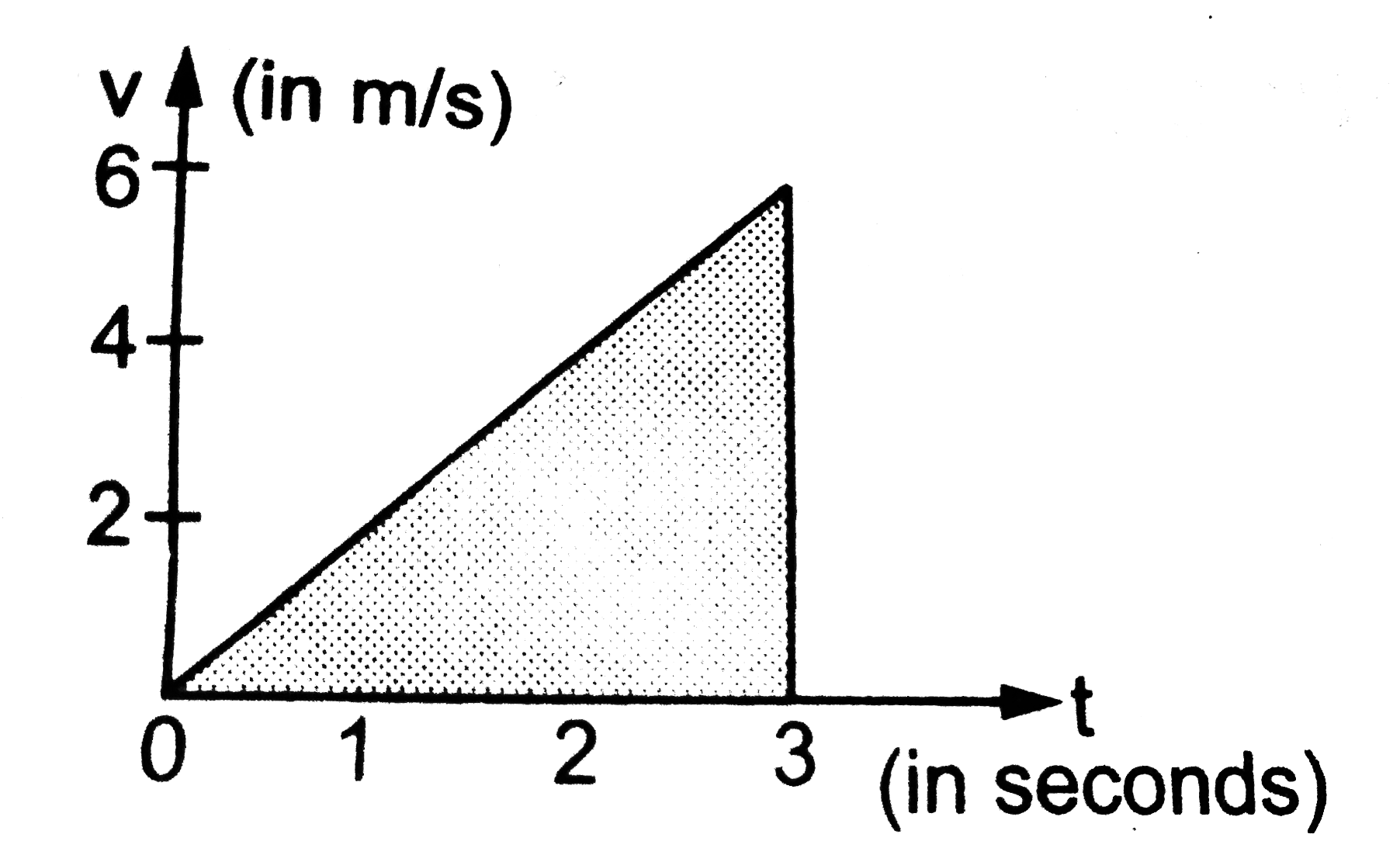
View SolutionFigure shows the speed versus time graph for a particle. Find the distance travelled by the particle during the time t=0 to t=3s.
View SolutionFor a gas sample with N_(0) number of molecules, function N(V) is given by: N(V) = (dN)/(dV) = ((3N_(0))/(V_(0)^(3)))V^(2) for 0 lt V lt V_(0) and N(V) = 0 for V gt V_(0) . Where dN is number of molecules in speed range V to V+ dV . The rms speed of the molecules is:
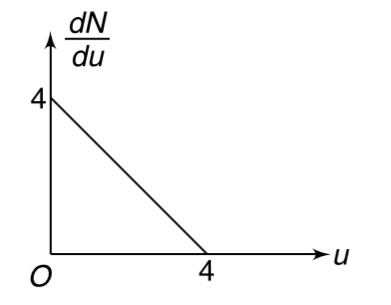
View SolutionA hypothetical gas sample has its molecular speed distribution graph as shown in the figure. The speed (u) and dNdu have appropriate units. Find the root mean square speed of the molecules. Do not worry about units.
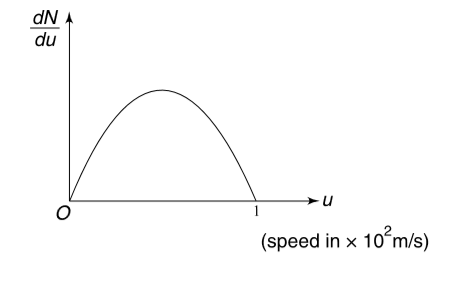
View SolutionThe speed distribution of molecules in a sample of a gas is shown in the figure. The graph between dNdu and u is a parabola and total number of molecules in the sample is N0.
(a) Calculate the rms speed of the molecules.
(b) Calculate the total translational kinetic energy of molecules if mass of the sample is 10 g.
View SolutionIf for an A.P., a= 10.5 , d= 0 , dn = 101, then what is the value of tn ?
View Solutionगैस का सेम्पल 0∘Cपर है। उसके अणु की गति दुगुनी करने के लिए ताप होगा -
View SolutionExplain that the following graph shows the values of P for ideal gas at constant temperature. beta=-(dV//dP)//V Displays the dress.
View SolutionDraw a graph showing the variation of decay rate (−dNdt) with number (N) of radioactive nuclei.
View SolutionA radioactive sample decays to form a stable nuclide. A graph showing variation of rate of disintegration (dNdt) of radioactive sample with time (t) is
View SolutionFigure shows the speed versus time graph for a particle. Find the distance travelled by the particle during the time t=0 to t=3s.

View SolutionGraph shows a hypothetical speed distribution. for a sample of N gas particles ( for v>v0,dNdV=0 )

View Solution
