Molar heat capacity of an ideal gas in the process PVx = constant , is given by : C=Rγ−1+R1−x. An ideal diatomic gas with CV=5R2 occupies a volume V1 at a pressure P1. The gas undergoes a process in which the pressure is proportional to the volume. At the end of the process the rms speed of the gas molecules has doubled from its initial value.
The molar heat capacity of the gas in the given process is :-Solution in Gujrati
3R
3.5R
4R
2.5R
The correct Answer is:A
PαV⇒PV−1=constant⇒x=−1
⇒C=CV+R2=5R2+R2=3R
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 04 (A)
48 Videos
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 04 (B)
15 Videos
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - ASSERTION-REASON
40 Videos
- CURRENT ELECTRICITYBOOK - ALLEN CHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
Two rods each of length L2 and coefficient of linear expansion α2 each are connected freely to a third rod of length L1 and coefficient of expansion α1 to form an isoscles triangle. The arrangement is supported on a knife-edge at the midpoint of L1 which is horizontal. what relation must exist between L1 and L2 so that the apex of the isoscles triangle is to remain at a constant height from the knife edge as the temperature changes ?
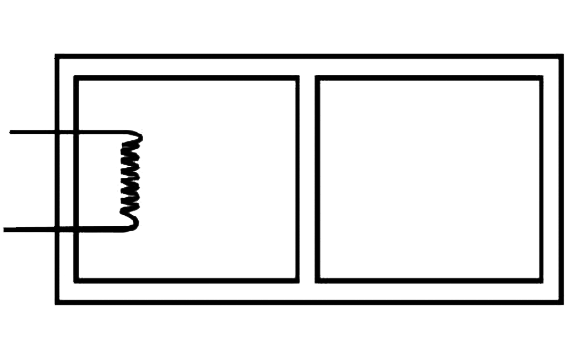
View SolutionThe rectangular box shown in Fig has partition which can slide without friction along the length of the box. Initially each of the two chambers of the box has one mole of a mono-atomic ideal gas (λ=5/3) at a pressure P0, volume V0 and temperature T0. The chamber on the left is slowly heated by an electric heater. The walls of the box and the lead wires of the heater is negligible. The gas in the left chamber expands pushing the partition until the final pressure in both chambers becomes 243P0/32. Determine (i) the final temperature of the gas in each chamber and (ii) the work done by the gas in the right chamber.
View SolutionStatement-1: A real gas behaves as an ideal gas at high temperature and low pressure .
Statement-2: Liquid state of an ideal gas is impossible.
View SolutionIn the Bohr's model of hy drogen atom, the electron moves around the nucleus in a circular orbit of radius 5×10−11m. Its time period is 1.5×10−16s. The current associated with the electron motion is:-
View SolutionAssertion : The difference in the value of acceleration due to gravity at pole and equator is proportional to square of angular velocity of earth.
Reason : the value of acceleration due to gravity is minimum at the equator and maximum at the pole.
View SolutionAn ideal diatomic gas with C_V = (5 R)/2 occupies a volume (V_(i) at a pressure (P_(i) . The gas undergoes a process in which the pressure is proportional to the volume. At the end of the process, it is found that the rms speed of the gas molecules has doubles from its initial value. Determine the amount of energy transferred to the gas by heat.
View SolutionFind the molar heat capacity (in terms of R) of a monoatomic ideal gas undergoing the process: PV1/2=constant?
View SolutionDuring an adiabatic process of an ideal gas, if P is proportional to (1)/(V^(1.5) , then the ratio of specific heat capacities at constant pressure to that at constant volume for the gas is
View SolutionAn ideal diatomic gas undergoes a process in which the pressure is proportional to the volume. Calculate the molar specific heat capacity of the gas for the process.
View SolutionAn ideal gas undergoes a process in which co-efficient of volume expansion of gas γ, varies with absolute temperature by the relation γ=2T. Let C is molar heat capacity in this process and Cp.CV are molar heat capacities at constant pressure and volume respectively. Then
View SolutionAn ideal diatomic gas with C_(V)=(5R)/(2) occupies a volume V_(1) at a pressure P_(1) . The gas undergoes a process in which the pressure is proportional to the volume. At the end of the process the rms speed of the gas molecules has doubled from its initial value. Heat supplied to the gas in the given process is
View SolutionMolar heat capacity of an ideal gas in the process PV^(x) = constant , is given by : C = (R)/(gamma-1) + (R)/(1-x) . An ideal diatomic gas with C_(V) = (5R)/(2) occupies a volume V_(1) at a pressure P_(1) . The gas undergoes a process in which the pressure is proportional to the volume. At the end of the process the rms speed of the gas molecules has doubled from its initial value. Heat supplied to the gas in the given process is :
View SolutionA monoatomic gas undergoes a process in which the pressure (P) and the volume (V) of the gas are related as PV−3=constant. What will be the molar heat capacity of gas for this process?
View SolutionAn ideal diatomic gas occupies a volume V_1 at a pressure P_1 The gas undergoes a process in which the pressure is proportional to the volume . At the end of process the root mean square speed of the gas molecules has doubled From its initial value then the heat supplied to the gas in the given process is
View SolutionAn ideal diatomic gas with CV=5R2 occupies a volume (Vi at a pressure (Pi. The gas undergoes a process in which the pressure is proportional to the volume. At the end of the process, it is found that the rms speed of the gas molecules has doubles from its initial value. Determine the amount of energy transferred to the gas by heat.
View SolutionAn ideal gas undergoes a process in which co-efficient of volume expansion of gas gamma , varies with absolute temperature by the relation gamma=(2)/(T) . Let C is molar heat capacity in this process and C_(p).C_(V) are molar heat capacities at constant pressure and volume respectively. Then
View Solution
