An ideal gas in enclosed in a tube and is held in the vertical position with the closed end upward. The length of pellet of mercury entrapping the gas is h=10 cm and the length of the tube occupied by gas is l=40 cm. Calculate the length occupied by the gas when it is turned through θ=60∘ and 90∘. Atmospheric pressure , H=76 cm of mercury.
_E01_265_Q01.png) Solution in Gujrati
Solution in Gujrati
The correct Answer is:37.2cm,34.7cm
For gas trapped in the tube P1V1=P2V2=P3V3
⇒(76−h)Al=(76−hcos60∘)Al=76×Al
⇒66×40=71×l'=76×l''l=37.2cm & l'=34.7cm
_E01_265_S01.png)
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 04 (B)
15 Videos
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 05 (A)
73 Videos
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - Comprehension Based Questions
66 Videos
- CURRENT ELECTRICITYBOOK - ALLEN CHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
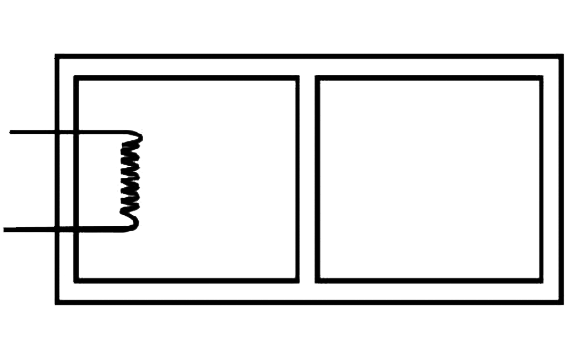
The rectangular box shown in Fig has partition which can slide without friction along the length of the box. Initially each of the two chambers of the box has one mole of a mono-atomic ideal gas (λ=5/3) at a pressure P0, volume V0 and temperature T0. The chamber on the left is slowly heated by an electric heater. The walls of the box and the lead wires of the heater is negligible. The gas in the left chamber expands pushing the partition until the final pressure in both chambers becomes 243P0/32. Determine (i) the final temperature of the gas in each chamber and (ii) the work done by the gas in the right chamber.
View SolutionAn aluminium sphere of 20cm diameter is heated from 0∘C to 100∘C. Its volume changes by (given that the coefficient of linear expanison for aluminium (αAl=23×10−6/0C)
View SolutionA certain amount of ice is supplied heat at a constant rate for 7 min. For the first one minute the temperature rises uniformly with time. Then it remains constant for the next 4 min and again the temperature rises at uniform rate for the last 2 min. Given Sice=0.5cal/g∘C,Lf=80cal/g.
The initial temperature of ice is
View SolutionIn the Bohr's model of hy drogen atom, the electron moves around the nucleus in a circular orbit of radius 5×10−11m. Its time period is 1.5×10−16s. The current associated with the electron motion is:-
View SolutionAssertion : The difference in the value of acceleration due to gravity at pole and equator is proportional to square of angular velocity of earth.
Reason : the value of acceleration due to gravity is minimum at the equator and maximum at the pole.
View SolutionAn open glass tube is immersed in mercury in such a way that a length of 8 cm extends above the mercury level. The open end of the tube is then closed and sealed and the tube is raised vertically up by additional 46 cm. what will be length of the air column above mercury in the above now ? (Atmospheric pressure = 76 cm of Hg)
View SolutionAn ideal gas is trapped between a mercury column and the closed lower end of a narrow vertical tube of uniform bore. The upper end of the tube is open to atmosphere (atmospheric pressure = 76 cm of Hg). The length of mercury and the trapped gas columns are 20 cm and 43 cm respectively. What will be the length of the gas column when the tube is titled slowly at constant temperature in a vertical plane through an angle of 60^(@) ?
View SolutionA Quill's tube of one metre is taken. A certain amount of ideal gas is trapped in it by a 20 cm length of Hg column. When the tube is held vertical with open end upwards, the length of the gas column is 50 cm. Find the pressure and length of the trapped gas, when the Quill's tube is kept in slanting position making 45^(@) with the vertical open and upwards. (Take atmospheric pressure as 76 cm of Hg and sqrt(2)=1.414) .
View SolutionIn the given figure, atmospheric pressure p0=1 atm and mercury column length is 9 cm. Pressure p of the gas enclosed in the tube is

View SolutionA glass tube open at both ends is immersed vertically in mercury in such a way that 13 cm length of the tube remains above the mercury surface. Now closing the upper end of the tube,it is raised through a further 35 cm. Determine the length of the air column above mercury in the closed tube. Atmospheric pressure =76 cmHg.
View SolutionAt standard condition 40 cm^3 of oxygen gas is introduced into a tube closed at one end and having a cross sectional area of 1.2 cm^2 . The open end is dipped in mercury and the tube is held vertically. The mercury meniscus in the tube stands at a height of 15.6 cm above the surface of mercury kept in the trough.IF the atmospheric pressure is 75.6 cm and the room temperature is 31^@C then what the length of the tube was filled with the gas?
View SolutionAn open glass tube is immersed in mercury in such a way that a length of 8 cm extends above the mercury level. The open end of the tube is then closed and sealed and the tube is raised vertically up by additional 46 cm. What will be length of the air column above mercury in the tube now ? (Atmospheric pressure = 76 cm of Hg)
View SolutionAn open glass tube is immersed in mercury in such a way that a length of 8 cm extends above the mercury level. The open end of the tube is then closed and sealed and the tube is raised vertically up by additional 46 cm. What will be length of the air column above mercury in the tube now? (atmospheric pressure =76 cm of Hg)
View SolutionAn ideal gas is trapped between a mercury column and the closed lower end of a narrow vertical tube of uniform bore. The upper end of the tube is open to the atmosphere. (Atmospheric pressure is 76 cm of mercury). The length of the mercury and the trapped gas columns are 20 cm and 43 cm, respectively. What will be the length of the gas column when the tube is tilted slowly in a vertical plane through an angle of 60∘. Assume the temperature to be constant.
View SolutionAn ideal gas is trapped between a mercury column and the closed end of a narrow vertical tube of uniform base containing the column. The upper end of the tube is open to the atmosphere. The atmospheric pressure equals 76 cm of mercury. The lengths of the mercury column and the trapped air column are 20 cm and 43 cm respectively. What will be the length of the air column when the tube is tilted slowly in a vertical plane through an angle of 60∘? Assume the temperature to remain constant.
View SolutionAn ideal gas is trapped between a mercury column and the closed lower end of a narrow vertical tube of uniform bore. The upper end of the tube is open to the atmosphere. (Atmospheric pressure is 76 cm of mercury). The length of the mercury and the trapped gas columns are 20 cm and 43 cm, respectively. What will be the length of the gas column when the tube is tilted slowly in a vertical plane through an angle of 60^(@) . Assume the temperature to be constant.
View Solution
