Two identical springs are fixed at one end and masses 1kg and 4kg are suspended at their other ends. They are both strethced down form their mean position and let go simultaneously. If they are in the same phase after every 4 seconds then the springs constant k is Solution in Gujrati
(a)π
(b)π2
(c)2π
(d)given data is insufficient
The correct Answer is:B
ω1=√km,ω2=√k4m=ω12
(ω1−ω2)t=0,2π,4π,……t=0
⇒t=2πω1−ω2=4⇒2π=4(ω1−ω2)
⇒π2=(ω1−ω2)⇒k=π2N/m
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise- 3 Match The Column
1 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Asseration & Reason
7 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-01
117 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
25 Videos
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
Similar Questions
Column-I gives different situtions in which bodes are floating in liquid. Column-II gives correspoding time periods of oscillation.
_E01_069_Q01.png)
A cube floating in liquid.
View SolutionStatement-1 : The motion of simple pedulum is simple harmonic only for a <<l.
Statement-2 : Motion of a simple pendulum is SHM for small angular displacement.
_E01_073_Q01.png)
View SolutionThe equation of motion of a particle of mass 1g is d2xdt2+π2x=0, where x is displacement (in m) from mean position. The frequency of oscillation is (in Hz)
View SolutionThe frequency of a radar is 780 MHz. After getting reflected from an approaching aeroplane, the apparent frequency is more than the actual frequency by 2.6 kHz. The aeroplane has a speed of
View SolutionChoose the correct statement:
View SolutionA light pulley is suspended at the lower end of a spring of constant k_(1) , as shown in figure. An inextensible string passes over the pulley. At one end of string a mass m is suspended, the other end of the string is attached to another spring of constant k_(2) . The other ends of both the springs are attached to rigid supports, as shown. Neglecting masses of springs and any friction, find the time period of small oscillations of mass m about equilibrium position.
View SolutionA spring of spring constant k stores 5 J of energy when stretched by 25 cm. It is kept vertical with one end fixed. A mass m is attached to the other end. It maskes 5 Oscillation per second. Then
View SolutionTwo identical springs of force constant "k" are joined one at the end of the other (in series). Find the effective force constant of the combination.
View SolutionFigure shows tow cases. In first case a spring (spring constant K) is pulled by two equal and opposite forces F at both ends and in second case is pulled by a force F at one end. Extensions (x) in the springs will be
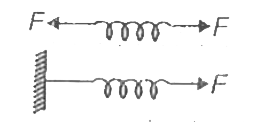
View SolutionThe force of two springs is constant k ,. One end of a spring is connected to the other end. The equivalent force of the combined spring system is constant a (k + kg),
View SolutionForce constants of two springs are k_1 and k_2 One end of a spring is connected with one end of the other. Equivalent force constant of the spring system will be
View SolutionForce constants of two springs are k_1 and k_2 . One end of a spring is connected with one end of the other. Equivalent force constant of the spring system will be
View SolutionOn a smooth inclined plane, a body of mass M is attached between two springs. The other ends of the springs are fixed to firm supports. If each spring has force constant K, the period of oscillation of the body (assuming the springs as massless) is :
View SolutionA block of mass .M. moving on the firctionless , horizontal surface collides with the spring of spring constant .k.. The other end of the spring is rigidly fixed to a vertical wall. If the spring is compressed by L, the maximum momentum of the block after collision is :
View SolutionA block of mass 'M' moving on the firctionless horizontal surface collides with the spring of spring constant 'k'. The other end of the spring is rigidly fixed to a vertical wall. If the spring is comressed by L, the maximum momentum of the block after collision is :
View SolutionA block of mass 'M' moving on the firctionless horizontal surface collides with the spring of spring constant 'k'. The other end of the spring is rigidly fixed to a vertical wall. If the spring is comressed by L, the maximum momentum of the block after collision is :
View Solution
