A cylindrical block of the density ρ is partically immersed in a liwuid of density 3ρ. The plane surface of the block remains parallel to the surface of the liquid. The height of the block is 60Cm. The block perform SHM when displaced form its mean position [Use g=9.8m/s2]Solution in Gujrati
the maximum amplitude is 20cm.
the maximum amplitude is 40cm
the time period will be 2π/7 seconds
none
The correct Answer is:A, C
When cylindrical block is partially immersed
FB=mg⇒3ρAyg=ρA(60×10−2)g
y=20cm
⇒ Maximum amplitude =20cm
_E01_053_S01.png)
Restoring force when it is slightly depressed by an amount of x.
F=−(ΔVσg)=−(Aσg)x
T=2π√mAσg=2π√ρAhA3ρg=2π√h3g
=2π√60×10−23×9.8=2π7s
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise- 3 Match The Column
1 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Asseration & Reason
7 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-01
117 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
25 Videos
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
Similar Questions
Column-I gives different situtions in which bodes are floating in liquid. Column-II gives correspoding time periods of oscillation.
_E01_069_Q01.png)
A cube floating in liquid.
View SolutionStatement-1 : The motion of simple pedulum is simple harmonic only for a <<l.
Statement-2 : Motion of a simple pendulum is SHM for small angular displacement.
_E01_073_Q01.png)
View SolutionThe equation of motion of a particle of mass 1g is d2xdt2+π2x=0, where x is displacement (in m) from mean position. The frequency of oscillation is (in Hz)
View SolutionThe frequency of a radar is 780 MHz. After getting reflected from an approaching aeroplane, the apparent frequency is more than the actual frequency by 2.6 kHz. The aeroplane has a speed of
View SolutionChoose the correct statement:
View SolutionA cylindrical tank has a hole of diameter 2r in its bottom. The hole is covered wooden cylindrical block of diameter 4r, height h and density ρ/3.

Situation I: Initially, the tank is filled with water of density ρ to a height such that the height of water above the top of the block is h1 (measured from the top of the block).
Situation II: The water is removed from the tank to a height h2 (measured from the bottom of the block), as shown in the figure. The height h2 is smaller than h (height of the block) and thus the block is exposed to the atmosphere.
Find the height of the water level h2 (in situation 2), for which the block remains in its origin) position whithout the application of any external force
View SolutionA wooden block performs SHM on a frictionaless surface with frequency, v_0 . The block carries a charge +Q on its surface. If now a uniform electric field vecE is switched-on as shown, then the SHM of the block will be
View SolutionA small block of wood of density 0.4×103kg/m3 is submerged in water at a depth of 2.9m. Find
(a) the acceletation of the block towards the surface when the block is released and
(b) the time for the block to reach the surface, Ignore viscosity.
View SolutionA wooden block performs SHM on a frictionless surface with frequency, v0. The block carries a charge +Q on its surface. If now a uniform electric field →E is switched on as shwon in figure., then the SHM of the block will be
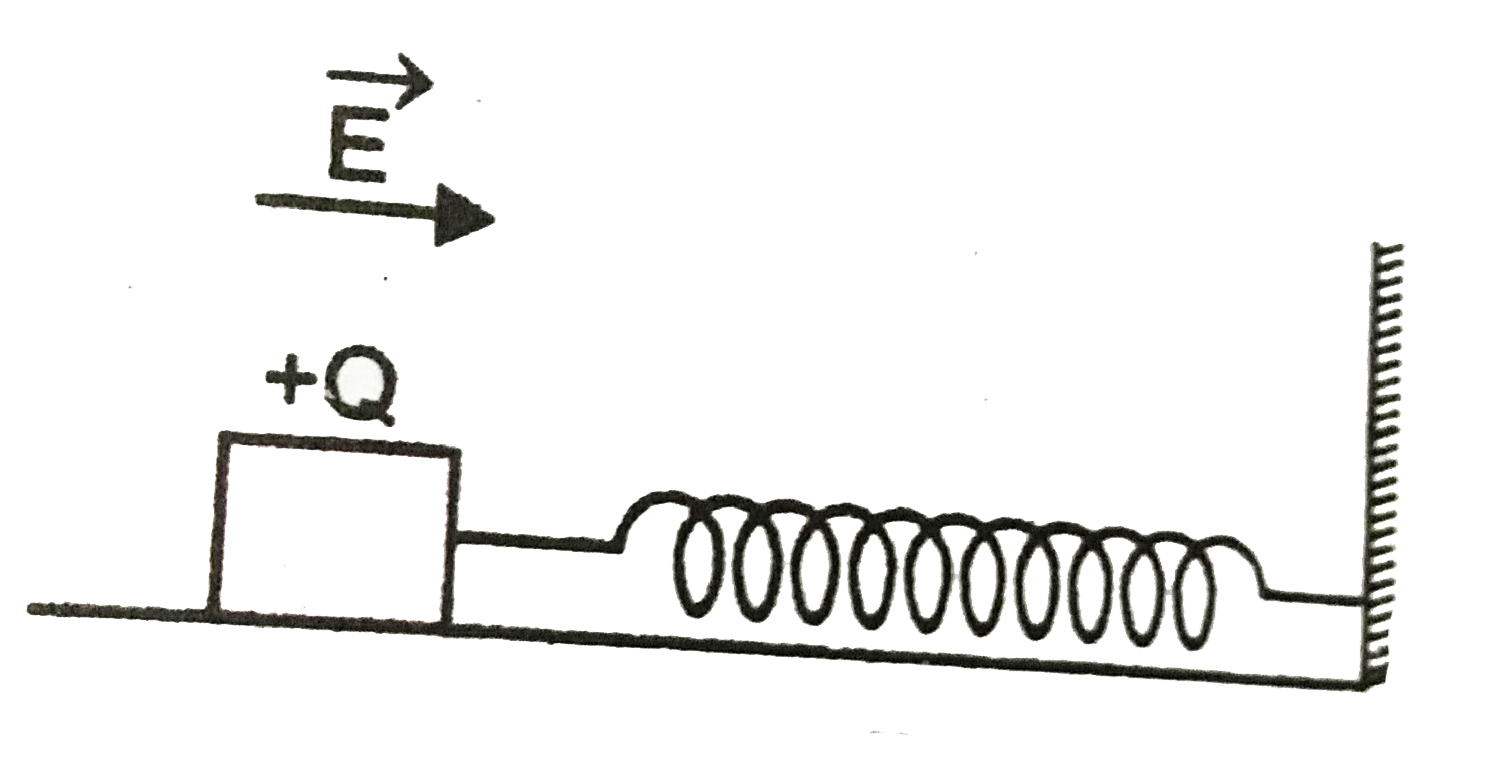
View Solution
Cylindrical block of area of cross-section A and of material of density ρ is placed in a liquid of density one third of density of block. The block compress in the spring is one-third of te length of the block. if acceleration due to gravity is g, the spring constant of the spring is
View SolutionA cubical block 'A' of mass m_(0)(=a^(3)rho=3 kg) of edge 'a' and density rho floats in a liquid of density 3rho . The lower surface of the cube just touches the free end of massless spring of spring of spring constant k(=a^(2)rho g) fixed at the bottom of the vessel. Another block 'B' of mass 'm' is lept over block 'A', so that is completely immersed in liquid without wetting the block 'B'. Then find the value of m in kg.
View SolutionA block of density ρ floats in a liquid with its one third volume immersed. The density of the liquid is
View SolutionA block hangs from a spring balance. The balance reads 40 N in air, 35 N when block is immersed in water and 25 N when block is immersed in another liquid. Find the density of block and other liquid.
View SolutionA block of density rho_(1) floats in two immiscible liquids of density 4 rho and 2 rho , such that (1/4)^(th) portion is in liquid of density 4 rho and remaining liquid of density 2 rho ,then rho_(1) =_________ g/(cm)^3 (Given rho=0.8g/(cm)^3 )
View SolutionIn Fig. , a rectangular block floats in a liquid . A block of mass m = 0.500 kg and density rho = 700 kg//m^(3) floats face down in a liquid of density rho_(f) = 1200 kg//m^(3) . What are the magnitude of the buoyant force on the block from the liquid , the weight of the liquid displaced by the block (liquid that would be in the space now occupied by the block ) , and the mass of that displaced liquid ? What fraction of the block's volume is submerged ? What fraction of its height is submerged ?
View SolutionA small block of wood of density 0.4xx10^(3)kg//m^(3) is submerged in water at a depth of 2.9m . Find (a) the acceletation of the block towards the surface when the block is released and (b) the time for the block to reach the surface, Ignore viscosity.
View Solution
