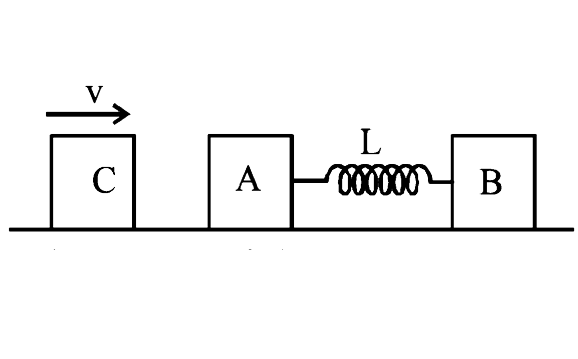
Two blocks A and B, each of mass m, are connected by a masslesss spring of natural length L and spring constant K. The blocks are initially resting on a smooth horizontal floor with the spring at its natural length, as shown in fig. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A and B, and collides elastically with A. Then
 Solution in Gujrati
Solution in Gujrati
The kinetic energy of the A-B system, at maximum compression of the spring, is zero.
The kintic energy of A-B system, at maximum compressioonof the sprin is mv24
The maximum compression of the spring is v√mk
The maximum compression of the spring is v√m2k
The correct Answer is:B, D
At maximum compression →vA=→vB & kinetic energy of A-B system will be minimum
so vA=vB=v2⇒KAB=14mv2
From energy conservation
12mv2=12m(v2)2+12m(v2)2+12kx2m⇒xm=v√m2k
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise- 3 Match The Column
1 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Asseration & Reason
7 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-01
117 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
25 Videos
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
Similar Questions
Column-I gives different situtions in which bodes are floating in liquid. Column-II gives correspoding time periods of oscillation.
_E01_069_Q01.png)
A cube floating in liquid.
View SolutionStatement-1 : The motion of simple pedulum is simple harmonic only for a <<l.
Statement-2 : Motion of a simple pendulum is SHM for small angular displacement.
_E01_073_Q01.png)
View SolutionThe equation of motion of a particle of mass 1g is d2xdt2+π2x=0, where x is displacement (in m) from mean position. The frequency of oscillation is (in Hz)
View SolutionThe frequency of a radar is 780 MHz. After getting reflected from an approaching aeroplane, the apparent frequency is more than the actual frequency by 2.6 kHz. The aeroplane has a speed of
View SolutionChoose the correct statement:
View SolutionTwo blocks A and B, each of mass m, are connected by a masslesss spring of natural length L and spring constant K. The blocks are initially resting on a smooth horizontal floor with the spring at its natural length, as shown in fig. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A and B, and collides elastically with A. Then

View SolutionTwo blocks A and H . each of mass m , are connected by a massless spring of natural length I . and spring constant K . The blocks are initially resting in a smooth horizontal floor with the spring at its natural length, as shown in Fig. A third identical block C , also of mass m , moves on the floor with a speed v along the line joining A and B . and collides elastically with A . Then
View SolutionTwo blocks A and B of masses m and 2m are connected by a massless spring of natural length L and spring constant k. The blocks are intially resting on a smooth horizontal floor with the spring at its natural length , as shown . A third identical block C of mass m moves on the floor with a speed v0 along the line joining A and B and collides elastically with A. FInd (a) the velocity of c.m. of system (blockA+B+spring) and (b) the minimum compression of spring.

View SolutionTwo identical blocks A and B , each of mass m resting on smooth floor are connected by a light spring of natural length L and spring constant k , with the spring at its natural length. A third identical block C (mass m ) moving with a speed v along the line joining A and B collides with A . The maximum compression in the spring is
View SolutionTwo blocks A and B each of mass m are connected by a massless spring of natural length L and spring constant k. The blocks are initially resting on a smooth horizontal floor with the spring at its natural length. A third identical block C also of mass m moves on the floor with a speed v along the line joining A and B and collides with A. Then
The kinetic energy of the A-B system at maximum compression of the spring is mv2/4
The maximum compression of the spring v√m/3k<br>Thek∈etice≠rgyoftheA−Bsystematmaxiμmcompression<br>Themaxiμmcoppressionofthespr∈gisvsqrt(m//k)
View SolutionTwo blocks A and B each of mass m are connected by a light spring of natural length L and spring constant k. The blocks are initially resting on a smooth horizontal floor with the spring at its natural length, as shown. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A to B and collides with A. Collision is elastic and head on. Then -
View SolutionTwo identical blocks A and B, each of mass m resting on smooth floor, are connected by a light spring of natural length L and the spring constant k, with the spring at its natural length. A third identical block C (mass m) moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is proportional to
View Solutionm द्रव्यमान के दो ब्लॉक A तथा B एक स्प्रिंग द्वारा जुड़े हैं। स्प्रिंग की वास्तविक लम्वाई L तथा स्प्रिंग नियतांक k है । प्रारम्भ में ब्लॉक एक चिकने क्षैतिज फर्श पर स्प्रिंग की स्वाभाविक लम्बाई के साथ चित्रानुसार विरामावस्था में हैं। A तथा B के समान ही m द्रव्यमान का एक अन्य ब्लॉक C, A तथा B को मिलाने वाली रेखा के अनुदिश v चाल से फर्श पर गति करता है तथा A से प्रत्यास्थ संघट्ट करता है, तब
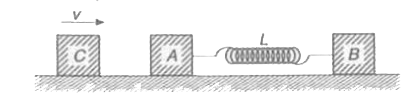
View SolutionTwo blocks A and B each of mass m are connected by a massless spring of natural length L and spring constant K. The blocks are initially resting on a smooth horizontal floor with the spring at its natural length, as shown in figure below. A third identical bloack C, also of mass m, moves on the floor with a speed v along the line joining A and B, and collides with A. Then :

View SolutionTwo bodies A and B of masses m and 2m respectively are placed on a smooth floor. They are connected by a light spring of stiffness k. A third body C of mass m moves with velocity v_(0) along the line joining A and B and collides elastically with A. If l_(o) be the natural length of the spring then find the minimum separation between the blocks.
View SolutionTwo identical blocks A and B , each of mass m resting on smooth floor are connected by a light spring of natural length L and spring constant k, with the spring at its natural length. A third identical block C (mass m) moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is
View Solution
