A body of mass m0 is placed on a smooth horizontal surface . The mass of the body is decreasing exponentially with disintegration constant , λ . Assuming that the mass is ejected backwards with a relative velocity u . If initially the body was at rest , the speed of body at time t is Solution in Gujrati
The correct Answer is:v=v0λt
N1=M0e−λt
Thus momentum of this mass
=Mv1v= velocity of mass at time t=M0e−λtv
Let at time dt defect mass is elected with relative velocity v0:v−v0+v
Linear momentum of M at time (t+dt)
=(M−dm)(v+dv)+dm(v−v0)
Since fext=0
(M−dm)(v+dv)+dm(v−v0)=Mv⇒(M−dm)dv=dmv0
⇒dv=v0dm(M−dm)⇒dvdt=dmdt(v0M−dm)=r.v0M−rdt
v=v0lnM0M0−rt. But M0−rt=M0e−λt
v=v0inM0M0e−λt=v0λt
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-05 [A]
39 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-05 [B]
12 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-04 [A]
20 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
25 Videos
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
Similar Questions
If a spring has time period T, and is cut into (n) equal parts, then the time period of each part will be.
View SolutionA particle of mass (m) is executing oscillations about the origin on the x axis. Its potential energy is V(x)=k|x|3 where k is a positive constant. If the amplitude of oscillation is a, then its time period (T) is.
View SolutionA particle simple harmonic motion completes 1200 oscillations per minute and passes through the mean position with a velocity 3.14ms−1. Determine displacement of the particle from its mean position. Also obtain the displacement equation of the particle if its displacement be zero at the instant t=0.
View SolutionThe frequency of a radar is 780 MHz. After getting reflected from an approaching aeroplane, the apparent frequency is more than the actual frequency by 2.6 kHz. The aeroplane has a speed of
View SolutionChoose the correct statement:
View SolutionA body of mass m_(1) collides elastically with another body of mass m_(2) at rest. If the velocity of m_(1) after collision is (2)/(3) times its initial velocity, the ratio of their masses is :
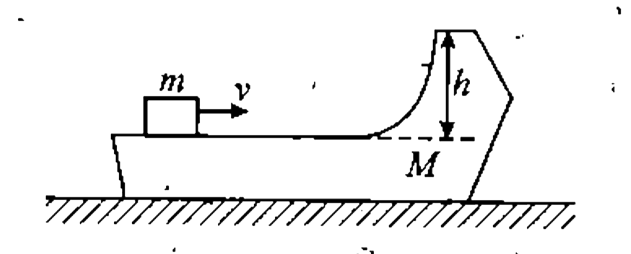
View SolutionA body of mass M with a small box of mass m placed on it rests on a smooth horizontal surface. The box is set in motion in the horizontal direction with a velocity u as shown in figure. To what height relative to the initial level will the box rise after breaking off from the body M? Assume all surfaces are frictionless.
View SolutionA body of mass m0 is placed on a smooth horizontal surface . The mass of the body is decreasing exponentially with disintegration constant , λ . Assuming that the mass is ejected backwards with a relative velocity u . If initially the body was at rest , the speed of body at time t is
View SolutionA body of mass m1 moving at a constant speed undergoes an elastic head on collision with a body of mass m2 initially at rest. The ratio of the kinetic energy of mass m1 after the collision to that before the collision is -
View SolutionA moving body with a mass m_(1) strikes a stationary body of mass m_(2) . The masses m_(1) and m_(2) should be in the ratio m_(1)/m_(2) so as to decrease the velocity of the first body 1.5 times assuming a perfectly clastic impact. Then the ratio m_(1)/m_(2) is
View SolutionA body of mass m is projected with intial speed u at an angle theta with the horizontal. The change in momentum of body after time t is :-
View SolutionIfv=c, the mass of the moving body, of rest mass 'm0' is _________________.
View SolutionA body of mass M moving with a speed u has a ‘head on’, perfectly elastic collision with a body of mass m initially at rest. If M > > m , the speed of the body of mass m after collision, will be nearly :
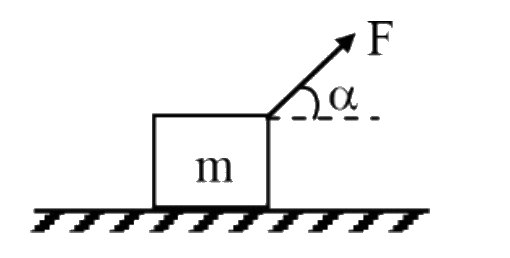
View SolutionAt the instant t=0, a force F=kt (k is a constant) acts on a small body of mass m resting on a smooth horizontal surface. The time, when the body leaves the surface is
View SolutionA body of mass 4 kg collides elastically with another body of mass 2 kg at rest. If time of collision is 0.02 sec and average impulse force acted on each body is 100N, find the velocity of 4kg body before and after collision (Assuming collision takes place on a smooth horizontal surface)
View SolutionA body of mass m_(0) is placed on a smooth horizontal surface . The mass of the body is decreasing exponentially with disintegration constant , lambda . Assuming that the mass is ejected backwards with a relative velocity u . If initially the body was at rest , the speed of body at time t is
View Solution
