A particle of mass (m) is executing oscillations about the origin on the x axis. Its potential energy is where k is a positive constant. If the amplitude of oscillation is a, then its time period (T) is.Solution in Gujrati
(a)porprotional to
(b)independent of a
(c)proportional to
(d)proportional to
The correct Answer is:A
Now, time period may depend on
Equating powers, we get
or
or
Hence,
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - MCQ s one or more than one correct answers
5 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Paragraph
3 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-05 [A]
39 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
25 Videos
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
Similar Questions
Three simple harmonic motions in the same direction having the same amplitude and same period are superposed. If each differ in phase from the next by 45∘, then
View SolutionA uniform thin cylindrical disk of mass M and radius R is attaached to two identical massless springs of spring constatn k which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. the unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity →V0=vacV0ˆi. The coefficinet of friction is μ.
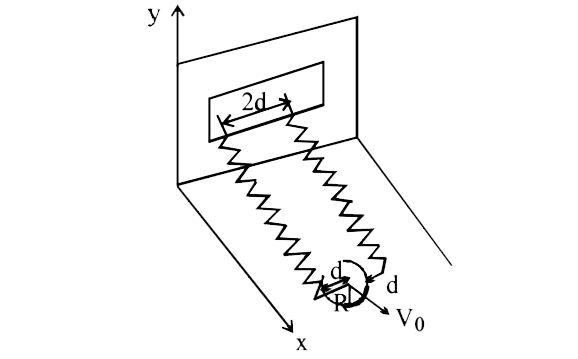
The net external force acting on the disk when its centre of mass is at displacement x with respect to its equilibrium position is.
View SolutionIf a spring has time period T, and is cut into (n) equal parts, then the time period of each part will be.
View SolutionThe frequency of a radar is 780 MHz. After getting reflected from an approaching aeroplane, the apparent frequency is more than the actual frequency by 2.6 kHz. The aeroplane has a speed of
View SolutionChoose the correct statement:
View SolutionA particle of mass (m) is executing oscillations about the origin on the (x) axis. Its potential energy is V(x)=k|x|3 where (k) is a positive constant. If the amplitude of oscillation is a, then its time period (T) is.
View SolutionA particle of m is executing SHMabout the origin on x- axis frequencxy √kaπm, where k is a constant and a is the amplitude Find its potential energy if x is the displecement at time t:
View SolutionA particle of mass m is executing oscillations about the origin on the x-axis, it's potential energy is U(x)=k|x|^(2) , where k is a positive constant, if the amplitude of oscillation is a, then it's time period T is
View SolutionA particle of mass m is executing oscillation about the origin on X- axis Its potential energy is V(x)=kIxI Where K is a positive constant If the amplitude oscillation is a, then its time period T is proportional
View Solutionm द्रव्यमान का एक कण X-अक्ष पर मूलबिंदु के परितः दोलन कर रहा है इसकी स्थितिज ऊर्जा U(x)=k|x|3 है जहाँ K एक धन नियतांक है यदि दोलन का आयाम a है तब इसका आवर्तकाल T :
View Solutionm द्रव्यमान का एक कण x-अक्ष पर मूल बिंदु के पारितः दोलन कर रहा है। इसकी स्थितिज ऊर्जा U(x)=k|x|3 है , जहाँ k एक धन नियतांक है। यदि दोलन का आयाम a है , तब इसका आवर्तकाल T
View SolutionA particle of mass m is executing oscillations about the origin of the x-axis with amplitude A. Its potential energy U(x)=ax^(4) , where a is a positive constant. What is the x - coordinate of the particle, where potential energy is one-third of the kinetic energy?
View SolutionA particle of mass m is executing oscillations about the origin on the x-axis. Its potential energy is V(x)=kx^(2) . Where k is a positive constant. If the amplitude of oscillation is a, then its time period T is……………
View SolutionA particle of mass m is executing S.H.M. about the origin along x-axis. The P.E. U(x)=kx3, where k is +ve constant. If the amplitude of oscillation is 'a', then time period T is proportional to :
View SolutionA particle of mass m is executing SHM about the origin on X-axis with frequency sqrt((ka)/(p m)) ,where k is a constant and a is the amplitude. Find its potential energy, if x is the displacement at time t
View SolutionA particle of mass m is executing oscillations about the origin on X-axis. Its potential energy isU(x)=−K|x|3, where K is a positive constant. If the amplitude of oscillation is a, then its time period T is:
View Solution
