Nuclei of radioactive element A are being produced at a constant rate. α. The element has a decay constant λ. At time t=0, there areN0 nuclei of the element.
Calculate the number N of nuclei of A at time t.Solution in Gujrati
The correct Answer is:(i) 1λ{α−(α−λN0)e−λt] (ii) (A) 32N0 B 2N0
(i) Let at time t, number of radioactive nuclei are N. Net rate of formation of nuclel of A
dNdt=α−λN⇒dNα−λN=dt⇒N∫N0dNα−λN=t∫0dt
Solving this equation, we get
N=1λ[α−(α−λN0)e−λt] .....(i)
(ii) (i) Substituting α=2λN0 and t−t1/2=ln(2)λ1n
equation (i) we get, N=32N0
(ii) Substituting α=2λN0 and t→∞ in equation (i), we get
N=αλ=2N0⇒N=2N0
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Solved Example
3 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - X Rays : Solved Example
2 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Paragraph
3 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
25 Videos
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
Similar Questions
A hydrogen like atom with atomic number Z is in an excited state of quantum number 2n. It can emit a maximum energy photon of 204 eV. If it makes a transition ot quantum state n, a photon of energy 40.8 eV is emitted. Find n, Z and the ground state energy (in eV) of this atom. Also calculate the minimum energy (in eV) that can be emitted by this atom during de-excitation. Ground state energy of hydrogen atom is – 13. 6 eV.
View SolutionWhen X-rays if wavelength 0.5Å pass through 10mm thick Al sheet than their intensity is reduced to one sixth . Find the absorption coefficient for Aluminium.
View SolutionA uniform thin cylindrical disk of mass M and radius R is attaached to two identical massless springs of spring constatn k which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. the unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity →V0=vacV0ˆi. The coefficinet of friction is μ.
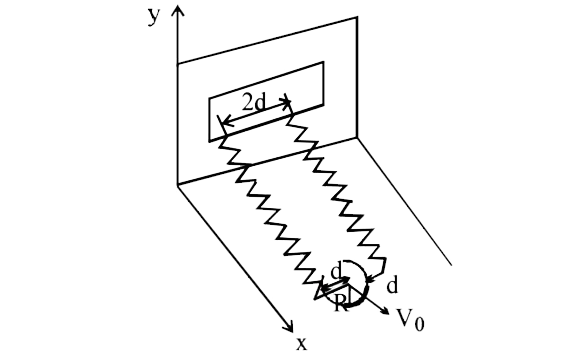
The net external force acting on the disk when its centre of mass is at displacement x with respect to its equilibrium position is.
View SolutionThe frequency of a radar is 780 MHz. After getting reflected from an approaching aeroplane, the apparent frequency is more than the actual frequency by 2.6 kHz. The aeroplane has a speed of
View SolutionChoose the correct statement:
View SolutionNuclei of a radioactive element A are being produced at a constant rate α. The element has a decay constant λ. At time t=0, there are N0 nuclei of the element.
(a) Calculate the number N of nuclei of A at time t.
(b) If α=2N0λ, calculate the number of nuclei of A after one half-life of A, and also the limiting value of N as t→∞.
View SolutionNuclei of a radioactive element X are being produced at a constant rate K and this element decays to a stable nucleus Y with a decay constant lambda and half-life T_(1//3) . At the time t=0 , there are N_(0) nuclei of the element X . The number N_(X) of nuclei of X at time t=T_(1//2) is .
View SolutionNuclei of a radioactive element X are being produced at a constant rate K and this element decays to a stable nucleus Y with a decay constant lambda and half-life T_(1//3) . At the time t=0 , there are N_(0) nuclei of the element X. The number N_(Y) of nuclei of Y at time t is .
View SolutionNuclei of radioactive element A are produced at rate 't^(2') (where t is time) at any time t . The element A has decay constant lambda . Let N be the number of nuclei of element A at any time t . At time t=t_(0), dN//dt is minimum. The number of nuclei of element A at time t=t_(0) is
View SolutionNuclei of a radioactive element A are being produced at a constant rate alpha . The element has a decay constant lambda . At time t=0, there are N_0 nuclei of the element . The number N of nuclei of A at time t is
View SolutionNuclei of a radioactive element 'A' are being produced at a constant rate alpha the element has a decay constant lambda At time t=0 there are N_(0) nuclei of the element The number of nuclei of A at time 't' is
View SolutionNuclei of a radioactive element 'A' are being produced at a constant rate α the element has a decay constant λ At time t=0 there are N0 nuclei of the element
If α=2N0λ the number of nuclei of A after t=ln2λ will become:
View SolutionNuclei of a radioactive element 'A' are being produced at a constant rate alpha the element has a decay constant lambda At time t=0 there are N_(0) nuclei of the element If alpha=2N_(0)lambda the number of nuclei of A after undergone radioactivity decay till time t=(l n2) / lambda :
View SolutionNuclei of a radioactive element 'A' are being produced at a constant rate alpha the element has a decay constant lambda At time t=0 there are N_(0) nuclei of the element If alpha = 4N_(0) lambda the number of nuclei of A when A has reached steady state:
View SolutionNuclei of a radioactive element 'A' are being produced at a constant rate, alpha . The element has a decay constant, lambda . At time, t = 0, there are N_(0) nuclei of the element. If alpha = 2N_(0)lambda the number of nuclei of A after one half life of A becomes
View Solution
