The potential energy of a partical varies as .
U(x)=E0 for 0≤x≤1
=0 for x>1
for 0≤x≤1 de- Broglie wavelength is λ1 and for x>1 the de-Broglie wavelength is λ2. Total energy of the partical is 2E0. find λ1λ2.Solution in Gujrati
The correct Answer is:√2
For 0≤x≤1,PE=E0
∴ Kinetic energy K1= Total energy −PE
=2E0−E0=E0∴Λ1=h√2m(2E0) …(i)
For x>1,PE=0
∴ Kinetic energy K2= Total energy =2E0
∴λ2=h√2m(2E0) ...(ii)
From equation (i) and (ii), we have λ1λ2=√2
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Solved Example
3 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - X Rays : Solved Example
2 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Paragraph
3 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
25 Videos
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
Similar Questions
A hydrogen like atom with atomic number Z is in an excited state of quantum number 2n. It can emit a maximum energy photon of 204 eV. If it makes a transition ot quantum state n, a photon of energy 40.8 eV is emitted. Find n, Z and the ground state energy (in eV) of this atom. Also calculate the minimum energy (in eV) that can be emitted by this atom during de-excitation. Ground state energy of hydrogen atom is – 13. 6 eV.
View SolutionWhen X-rays if wavelength 0.5Å pass through 10mm thick Al sheet than their intensity is reduced to one sixth . Find the absorption coefficient for Aluminium.
View SolutionA uniform thin cylindrical disk of mass M and radius R is attaached to two identical massless springs of spring constatn k which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. the unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity →V0=vacV0ˆi. The coefficinet of friction is μ.
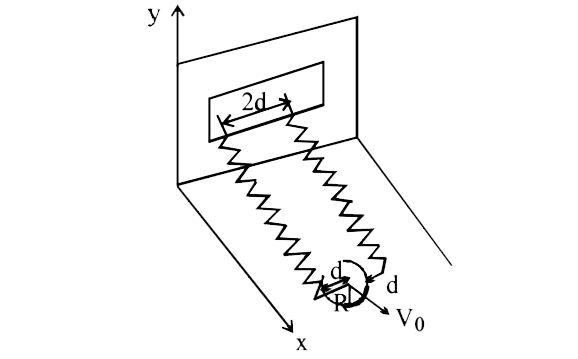
The net external force acting on the disk when its centre of mass is at displacement x with respect to its equilibrium position is.
View SolutionThe frequency of a radar is 780 MHz. After getting reflected from an approaching aeroplane, the apparent frequency is more than the actual frequency by 2.6 kHz. The aeroplane has a speed of
View SolutionChoose the correct statement:
View SolutionIf the two roots of the equation (λ−2)(x2+x+1)2−(λ+2)(x4+x2+1) are real and equal for λ=λ1,λ2 then λ1+λ2=0 (b) |λ1−λ2|=6 (c) λ1+λ2=32 (d) all of these
View SolutionThe energy of a photon is equal to the kinetic energy of a proton. The energy of the photon is E. Let lambda_1 be the de-Broglie wavelength of the proton and lambda_2 be the wavelength of the photon. The ratio (lambda_1)/(lambda_2) is proportional to (a) E^0 (b) E^(1//2) (c ) E^(-1) (d) E^(-2)
View SolutionThe potential energy of a partical varies as
. U(x)=E0for0≤x≤1 =0forx>1For0≤x≤1, de- Broglie wavelength is λ1 and for xgt the de-Broglie wavelength is λ2. Total energy of the partical is 2E_0. find λ1λ2.
View SolutionThe potential energy of a particle of mass m is given by U(x){E00≤x<10x>1
λ1 and λ2 are the de-Broglie wavelength of the particle, when 0≤x≤1 and x>1 respectively. If the total energy of particle is 2E0, then the ratio λ1λ2 will be
View SolutionThe potential energy of particle of mass m varies as
U(x)={E0for0≤x≤10 for >1
The de Broglie wavelength of the particle in the range 0≤x≤1 is λ1 and that in the range x>1 is λ2.
If the total of the particle is 2E0, find λ1/λ2.
View Solutionf(x)⎧⎪⎨⎪⎩2x,ifx<00,if0≤x≤14x,ifx>1
View SolutionThe potential energy of a particle of mass m is given by U(x)=E00≤x≤10 x>1 λ1 and λ2 are the de-Broglie wavelengths of the particle, when 0≤x≤1 and x > 1 respectively. If the total energy of particle is 2E0. find (λ1/λ2)2
View Solutionthe energy of photon is equal to the kinetic energy of a porton,If lambda_1 is the De-Broglie wavelength of a proton, lambda_2 the wavelength associated with the proton and if the energt of the protonis E, then (lamda_1//lambda_2) is proportional to
View Solutionकिसी m द्रव्यमान के कण की स्थितिज ऊर्जा निम्न प्रकार दी जाती है
U(X)={E00≤x≤10x>1
0≤x≤1 एवं x>1 के लिए डी - ब्रोग्ली तरंग दैर्ध्य क्रमशः λ1 तथा λ2 है। यदि कण की कुल ऊर्जा 2E0 है तो अनुपात λ1λ2 होगा
View Solutionकिसी m द्रव्यमान के कण की स्थितिज ऊर्जा निम्न प्रकार दी जाती है
U(x)={E00≤x≤10x>1
0≤x≤1 एवं x > 1 के लिये दे-ब्रोग्ली तरंगदैर्ध्य क्रमशः λ1 तथा λ2 हैं। यदि कण की कुल ऊर्जा 2E0 है, तो अनुपात λ1λ2 होगा
View Solutionf(x)=⎧⎪⎨⎪⎩2x,ifx<00,if0≤x≤14x,ifx>1
View Solution
