A uniform thin cylindrical disk of mass M and radius R is attaached to two identical massless springs of spring constatn k which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. the unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity →V0=vacV0ˆi. The coefficinet of friction is μ.
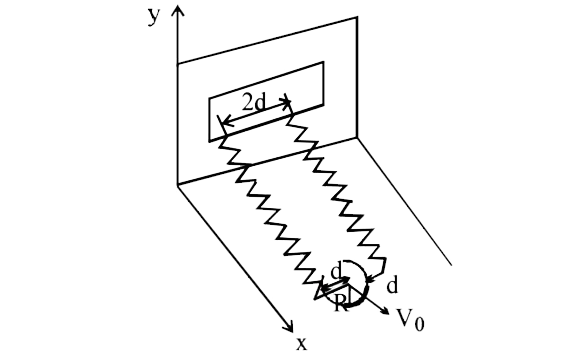
The net external force acting on the disk when its centre of mass is at displacement x with respect to its equilibrium position is.Solution in Gujrati
−kx
−2kx
−2kx3
−4kx3
The correct Answer is:D
For linear motion of disc
Fnet=Ma=−2kx+f
where f= frictional force
For rolling motion
fR=−(MR22)(α)=−(Ma2)R
⇒f=−Ma2=−Fext2
Therefore Fext=−2kx−Fext2=−4kx3
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Subjective
30 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Solved Example
3 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - MCQ s one or more than one correct answers
5 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
25 Videos
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
Similar Questions
Two masses m1 and m2 concute a high spring of natural length l0 is compressed completely and tied by a string. This system while conving with a velocity v0 along +ve x-axis pass thorugh the origin at t=0, at this position the string sanps, Position of mass m1 at time t is given by the equation x1t=v0(A/1−cosωt). Calculate (i) position of the particle m2 as a funcation of time, (ii) l0 in terms of A.
View SolutionA hydrogen like atom with atomic number Z is in an excited state of quantum number 2n. It can emit a maximum energy photon of 204 eV. If it makes a transition ot quantum state n, a photon of energy 40.8 eV is emitted. Find n, Z and the ground state energy (in eV) of this atom. Also calculate the minimum energy (in eV) that can be emitted by this atom during de-excitation. Ground state energy of hydrogen atom is – 13. 6 eV.
View SolutionThree simple harmonic motions in the same direction having the same amplitude and same period are superposed. If each differ in phase from the next by 45∘, then
View SolutionThe frequency of a radar is 780 MHz. After getting reflected from an approaching aeroplane, the apparent frequency is more than the actual frequency by 2.6 kHz. The aeroplane has a speed of
View SolutionChoose the correct statement:
View SolutionA uniform thin cylindrical disk of mass M and radius R is attaached to two identical massless springs of spring constatn k which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. the unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity vecV_0 = vacV_0hati. The coefficinet of friction is mu. The net external force acting on the disk when its centre of mass is at displacement x with respect to its equilibrium position is.
View SolutionA uniform thin cylindrical disk of mass M and radius R is attaached to two identical massless springs of spring constatn k which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. the unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity vecV_0 = vacV_0hati. The coefficinet of friction is mu. The centre of mass of the disk undergoes simple harmonic motion with angular frequency omega equal to -
View SolutionA uniform thin cylindrical disk of mass M and radius R is attaached to two identical massless springs of spring constatn k which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. the unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity vecV_0 = vacV_0hati. The coefficinet of friction is mu. The maximum value of V_0 for whic the disk will roll without slipping is-
View SolutionOn a smooth inclined plane, a body of mass M is attached between two springs. The other ends of the springs are fixed to firm supports. If each spring has force constant K , the period of oscillation of the body (assuming the springs as massless) is
View SolutionOn a smooth inclined plane a body of mass M is attached between two springs. The other ends of the springs are fixed to firm supports. If each spring has a force constant k, the period of oscilation of the body is (assuming the spring as massless)
View Solutionदीवार पर जड़े स्प्रिंग नियतांक k वाले दो समरूप स्प्रिंगों से R त्रिज्या व M द्रव्यमान वाले बेलनाकार चकती चित्रानुसार जुड़ी है। दोनों स्प्रिंगे बेलनाकार चकती के केंद्र से d दूरी पर स्थित एक्सल के दोनों ओर जुड़े हैं। एक्सल तथा स्प्रिंग क्षैतिज तल में है तथा एक्सल भारहीन है। प्रत्येक स्प्रिंग की लम्बाई L है। साम्यावस्था में चकती का द्रव्यमान केंद्र दीवार से L दूरी पर है। चकती बिना फिसले v0=v0ˆi से लुढ़कती है तब घर्षण गुणांक μ है। चकती पर कार्य करने वाला परिणामी बाह्य बल, जबकि चकती का द्रव्यमान केंद्र माध्य स्थिति से x दूरी पर होगा-
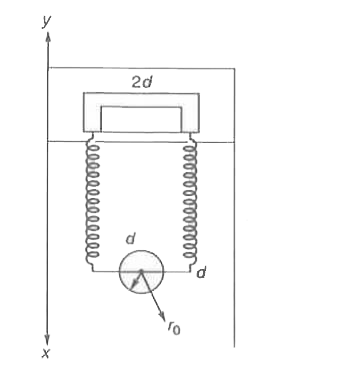
View Solutionदीवार पर जड़े स्पिरंग नियतांक k वाले दो समरूप स्पि्रंगों से R त्रिज्या व M द्रव्यमान वाले बेलनाकार चकती चित्रानुसार जुड़ी है। दोनों स्पि्रंगें बेलनाकार चकती के केंद्र से d दूरी पर स्थित एक्सल के दोनों ओर जुड़े हैं। एक्सल तथा स्पि्रंग क्षेतिज तल में है तथा एक्सल भारहीन है। प्रत्येक स्पि्रंग की लम्बाई L है। साम्यावस्था में चकती का दव्यमान केंद्र दीवार से L दूरी पर है। चकती बिना फिसले v0=v0ˆi से लुढ़कती है तब घर्षण गुणांक μ है।
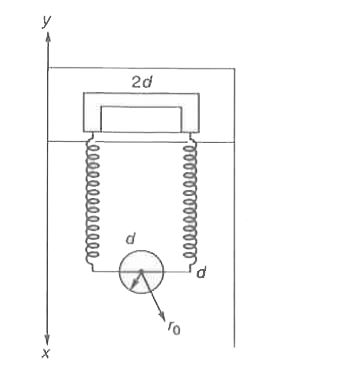
सरल आवर्त गति करती हुई चकती के द्रव्यमान केंद्र की कोणीय आवृत्ति ω का मान होगा
View Solutionदीवार पर जड़े स्पिरंग नियतांक k वाले दो समरूप स्पि्रंगों से R त्रिज्या व M द्रव्यमान वाले बेलनाकार चकती चित्रानुसार जुड़ी है। दोनों स्पि्रंगें बेलनाकार चकती के केंद्र से d दूरी पर स्थित एक्सल के दोनों ओर जुड़े हैं। एक्सल तथा स्पि्रंग क्षेतिज तल में है तथा एक्सल भारहीन है। प्रत्येक स्पि्रंग की लम्बाई L है। साम्यावस्था में चकती का दव्यमान केंद्र दीवार से L दूरी पर है। चकती बिना फिसले v0=v0ˆi से लुढ़कती है तब घर्षण गुणांक μ है।
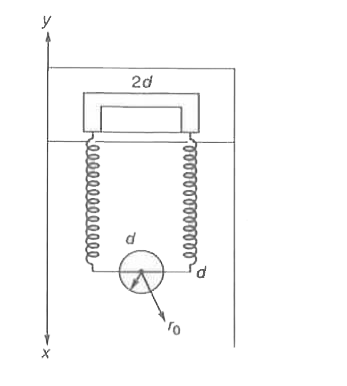
v0 का वह अधिकतम मान जिसके लिए चकती बिना फिसले लुढ़क जाएगी, है
View SolutionOn a smooth inclined plane, a body of mass M is attached between two springs. The other ends of the springs are fixed to firm supports. If each spring has force constant K, the period of oscillation of the body (assuming the springs as massless) is :
View SolutionOn a smooth inclined plane, a body of mass M is attached between two springs. The other ends of the springs are fixed to firm supports. If each spring has force constant K , the period of oscillation of the body (assuming the springs as massless) is

View SolutionA particle of mass m is attached to three identical massless springs of spring constant k as shown in the m 135 figure. The time period of vertical oscillation of the particle is

View Solution
