A particle which is moving along x-axis has acceleration at any time t like a(t)=(12t2−30t)m/s2.At t=0, velocity of particle is 7 m/s and at t=1 sec, particle is at x=6m. Choose the CORRECT function for position at any time t. Solution in Gujrati
The correct Answer is:0.45
Step by step video & image solution for A particle which is moving along x-axis has acceleration at any time t like a(t)=(12t^2-30t)m//s^2.At t=0, velocity of particle is 7 m/s and at t=1 sec, particle is at x=6m. Choose the CORRECT function for position at any time t. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - CHEMISTRY SECTION-I
20 Videos
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - CHEMISTRY SECTION-II
16 Videos
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS SECTION-I
20 Videos
- SEQUENCE AND PROGRESSIONBOOK - ALLEN CHAPTER - SEQUENCE AND PROGRESSIONEXERCISE - Exercise (JA)
10 Videos
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - MATHEMATICS
136 Videos
Similar Questions
Which of the following statements is/are incorrect -
View SolutionThe molar mass of a substance , each molecule of which contains 9 C atoms , 13 H-atoms and 3.32×10−23 g of other component is (NA=6.022×1023)
View SolutionGiven arrangement is in equilibrium and elongation in spring is 1cm. Tension in string AD is T1, in string BD is T2 and is string CD is T3.Choose correct values of T1,T2andT3:
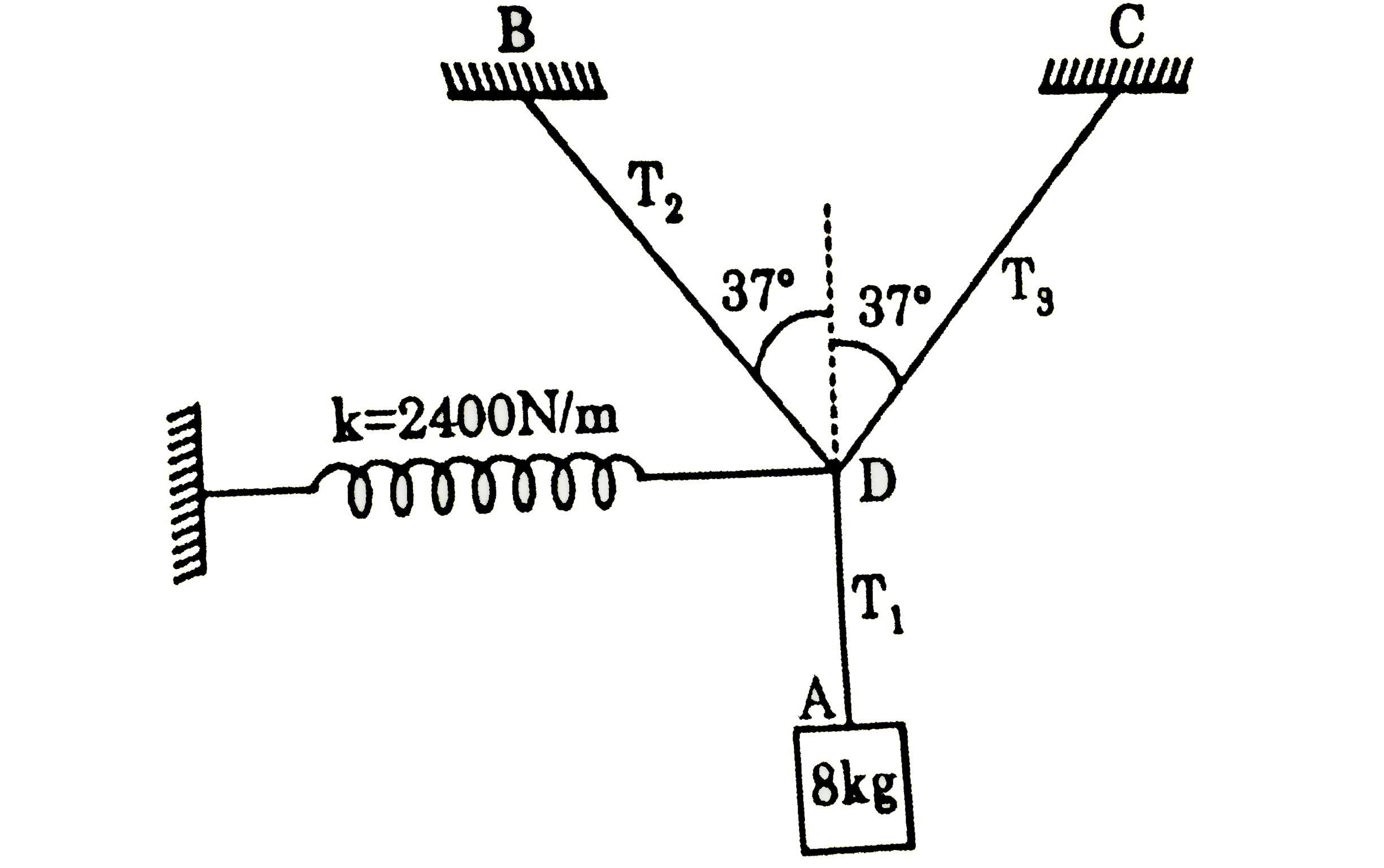
View SolutionThe minimum value of the sum of real numbers a−5,a−4,3a−3,1,a8 and a10 with a>0 is
View SolutionIf a be sum of the odd numbered terms and b the sum of even numbered terms of the expansion (1+x)n,n ε N then (1−x2)n is equal to
View SolutionVelocity (in m/s) of a particle moving along x-axis varies with time as, v= (10+ 5t -t^2) At time t=0, x=0. Find (a) acceleration of particle at t = 2 s and (b) x-coordinate of particle at t=3s
View SolutionThe coordinates of a particle moving in x-y plane at any time t are (2 t, t^2). Find (a) the trajectory of the particle, (b) velocity of particle at time t and (c) acceleration of particle at any time t.
View SolutionThe position of a particle moving on the x-axis is given by x=t^(3)+4t^(2)-2t+5 where x is in meter and t is in seconds (i) the velocity of the particle at t=4 s is 78 m//s (ii) the acceleration of the particle at t=4 s is 32 m//s^(2) (iii) the average velocity during the interval t=0 to t=4 s is 30 m//s (iv) the average acceleration during the interval t=0 to t=4 s is 20 m//s^(2)
View SolutionA particle is moving along a straight line along x-zxis with an initial velocity of 2m/s towards positive x-axis. A constant acceleration of 0.5m/s2 towards negative x-axis starts acting on particle at t=0. Find velocity (in m/s) of particle at t=2s.
View SolutionLet s(t)=t3−6t2 be the position function of a particle moving along an s-axis, where s is in meters and t is in sec. find the instantaneous acceleration a(t) and show the graph of acceleration versus time.
View SolutionThe acceleration-time graph of a particle moving along x-axis is shown in the figure. If the particle starts with velocity 3 m/s at t = 0, find the velocity of particle at t = 4 s.
View SolutionA particle moves along x-axis and its acceleration at any time t is a = 2 sin (πt), where t is in seconds and a is in m/s2 . The initial velocity of particle (at time t = 0) is u = 0.
Q. Then the distance travelled (in meters) by the particle from time t = 0 to t = 1 s will be :
View SolutionA particle moves along x-axis and its acceleration at any time t is a = 2 sin ( pit ), where t is in seconds and a is in m/ s^2 . The initial velocity of particle (at time t = 0) is u = 0. Q. Then the distance travelled (in meters) by the particle from time t = 0 to t = t will be :
View SolutionA particle moves along x-axis and its acceleration at any time t is a = 2 sin (πt), where t is in seconds and a is in m/s2 . The initial velocity of particle (at time t = 0) is u = 0.
Q. Then the magnitude of displacement (in meters) by the particle from time t = 0 to t = t will be :
View Solution[" Velocity of a particle moving along "x" -axis "],[" as a function of time is given as "v=(4-],[t^(2))m/s," where "t" is time in second.The "],[" displacement of particle during "t=0s" to "t],[=1s" is "]
View SolutionA particle moves along a horizontal line such that its position at any time t is given by s(t)=t3−6t2+9t+1, s in meters and t in seconds.
At what time the particle is at rest?
View Solution
