The velocity of a particle moving along positive X-axis varies as v=α√x where α is a constant.if particle is at x=0 at t=0 , what will be the average velocity of particle during the time it moves a distance S ?Solution in Gujrati
The correct Answer is:0.32
Step by step video & image solution for The velocity of a particle moving along positive X-axis varies as v=alphasqrtx where alpha is a constant.if particle is at x=0 at t=0 , what will be the average velocity of particle during the time it moves a distance S ? by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - CHEMISTRY SECTION-I
20 Videos
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - CHEMISTRY SECTION-II
16 Videos
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS SECTION-I
20 Videos
- SEQUENCE AND PROGRESSIONBOOK - ALLEN CHAPTER - SEQUENCE AND PROGRESSIONEXERCISE - Exercise (JA)
10 Videos
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - MATHEMATICS
136 Videos
Similar Questions
Which of the following statements is/are incorrect -
View SolutionThe molar mass of a substance , each molecule of which contains 9 C atoms , 13 H-atoms and 3.32×10−23 g of other component is (NA=6.022×1023)
View SolutionGiven arrangement is in equilibrium and elongation in spring is 1cm. Tension in string AD is T1, in string BD is T2 and is string CD is T3.Choose correct values of T1,T2andT3:
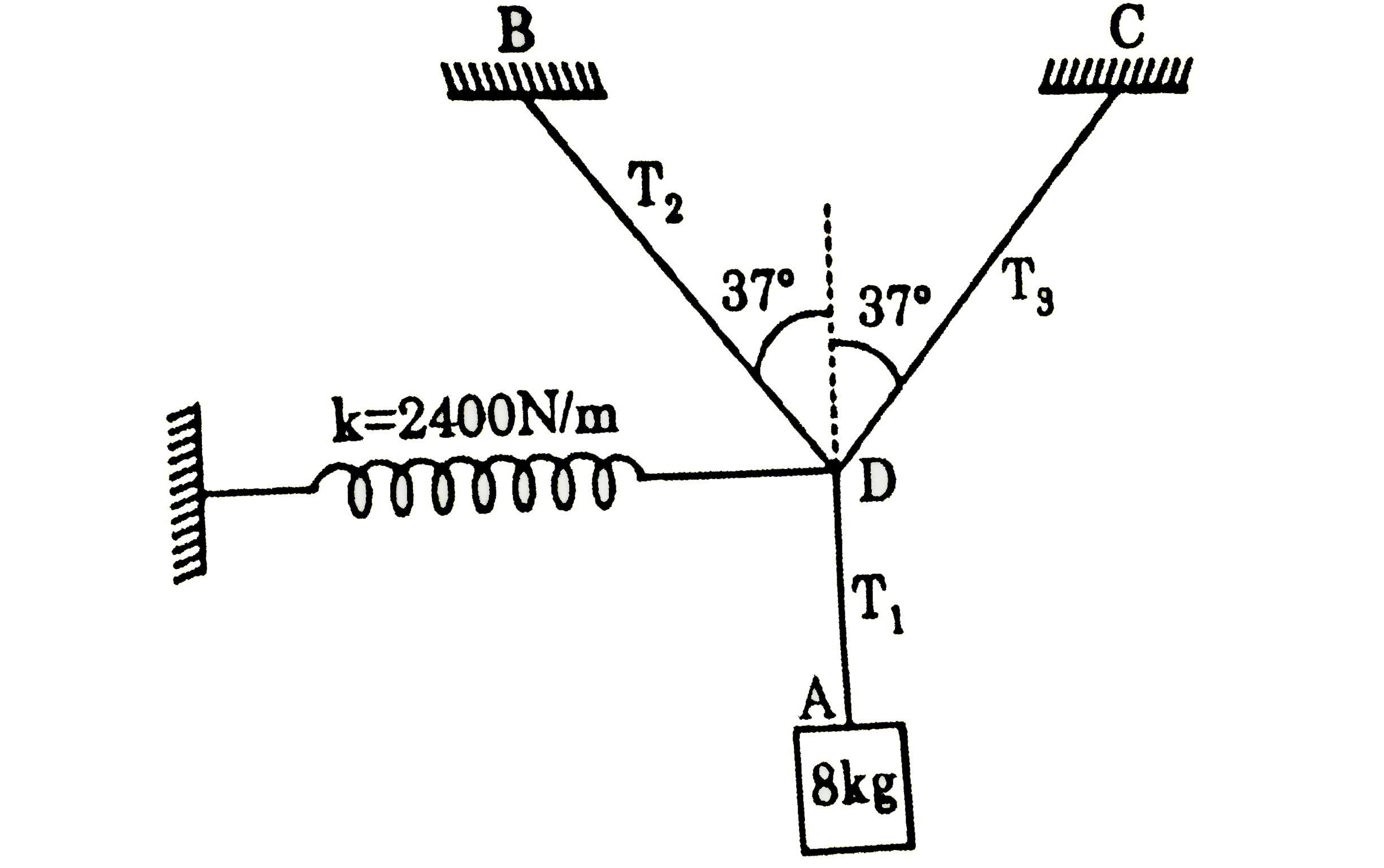
View SolutionThe minimum value of the sum of real numbers a−5,a−4,3a−3,1,a8 and a10 with a>0 is
View SolutionIf a be sum of the odd numbered terms and b the sum of even numbered terms of the expansion (1+x)n,n ε N then (1−x2)n is equal to
View SolutionA particle located at x = 0 at time t = 0 , starts moving along with the positive x-direction with a velocity 'v' that varies as v = a sqrt(x) . The displacement of the particle varies with time as
View SolutionThe velocity of a particle moving in the positive direction of x-axis veries as v=10√x. Assuming that at t=0, particle was at x=0
View SolutionThe velocity of a particle moving in the positive direction of X-axis varies as v=5sqrt(x) . Assuming that at t = 0, particle was at x = 0. What is the acceleration of the particle ?
View SolutionIf the velocity of a particle moving along x-axis is given as v=(3t2−2t) and t=0, x=0 then calculate position of the particle at t=2sec.
View SolutionA particle located at x = 0 at time t = 0, starts moving along the positive x-direction with a velocity that varies as v=psqrtx . The displacement of the particle varies with time as (where, p is constant)
View SolutionAt t = 0 a particle is in position x = 0. Now the particle v=alphasqrtx ( alpha Hall constant) began to move along the positive x-axis with velocity. How does the displacement of an object change over time?
View SolutionThe velocity of a particle moving along the positive direction of x-axis is v= Asqrt(x) , where A is a positive constant. At time t = 0 , the displacement of the particle is taken as x = 0 . (i) Express velocity and acceleration as functions of time , and (ii) find out the average velocity of the particle in the period when it travels through a distance s ?
View SolutionA particle located at x = 0 at time t=0 starts moving along positive x-direction with velocity v that varies as v=a√x. The displacement of the particle varies with time as :
View SolutionA particle of unit mass is moving along x-axis. The velocity of particle varies with position x as v(x). =αx−β (where α and β are positive constants and x>0 ). The acceleration of the particle as a function of x is given as
View SolutionA particle located at position x=0, at time t=0, starts moving along the positive x-direction with a velocity v2=αx (where alpha is a positive constant). The displacement of particle is proportional to
View SolutionThe velocity of a particle moving in the positive direction of X-axis varies as v=5√x. Assuming that at t = 0, particle was at x = 0. What is the acceleration of the particle ?
View Solution
