The speed (v) and time (t) for an object moving along straight line are related as t2+100=2vt where v is in meter/second and t is in second. Find the possible positive values of v. Solution in Gujrati
(i) y=e−x=ez where z=−x so dydx=dydz×dzdx=(ez)(−1)=−ez=−e−x
(ii) y=4sin3x=4sinz where z=3x so dydx=dydz×dzdx=4(cosz)(3)=12cos3x
(iii) y=4ex2−2x=4ez where z=x2−2x so dydx=dydz×dzdx=4(ez)(2x−2)=(8x−x)ex2−2x
Topper's Solved these Questions
- BASIC MATHSBOOK - ALLEN CHAPTER - BASIC MATHSEXERCISE - Exercise-02
53 Videos
- BASIC MATHSBOOK - ALLEN CHAPTER - BASIC MATHSEXERCISE - Exersice-03
7 Videos
- AIIMS 2019BOOK - ALLEN CHAPTER - AIIMS 2019EXERCISE - PHYSICS
39 Videos
- CIRCULAR MOTIONBOOK - ALLEN CHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (J-A)
6 Videos
Similar Questions
Two vectors →A and →B are such that →A+→B=→A−→B. Then
View SolutionThe direction of the angular velocity vector is along
View SolutionA simple pendulum executing SHM in a straight line has zero velocity at 'A' and 'B' whose distances form 'O' in the same line OAB are 'a' and 'b'. If the velocity half wat between them is 'v' then its time period is
View SolutionA ball of mass (m)0.5kg is attached to the end of a string having length (L)0.5m. The ball is rotated on a horizontal circular path about vertical axis. The maximum tension that the string can bear is 324N. The maximum possible value of angular velocity of ball (radian/s) is -
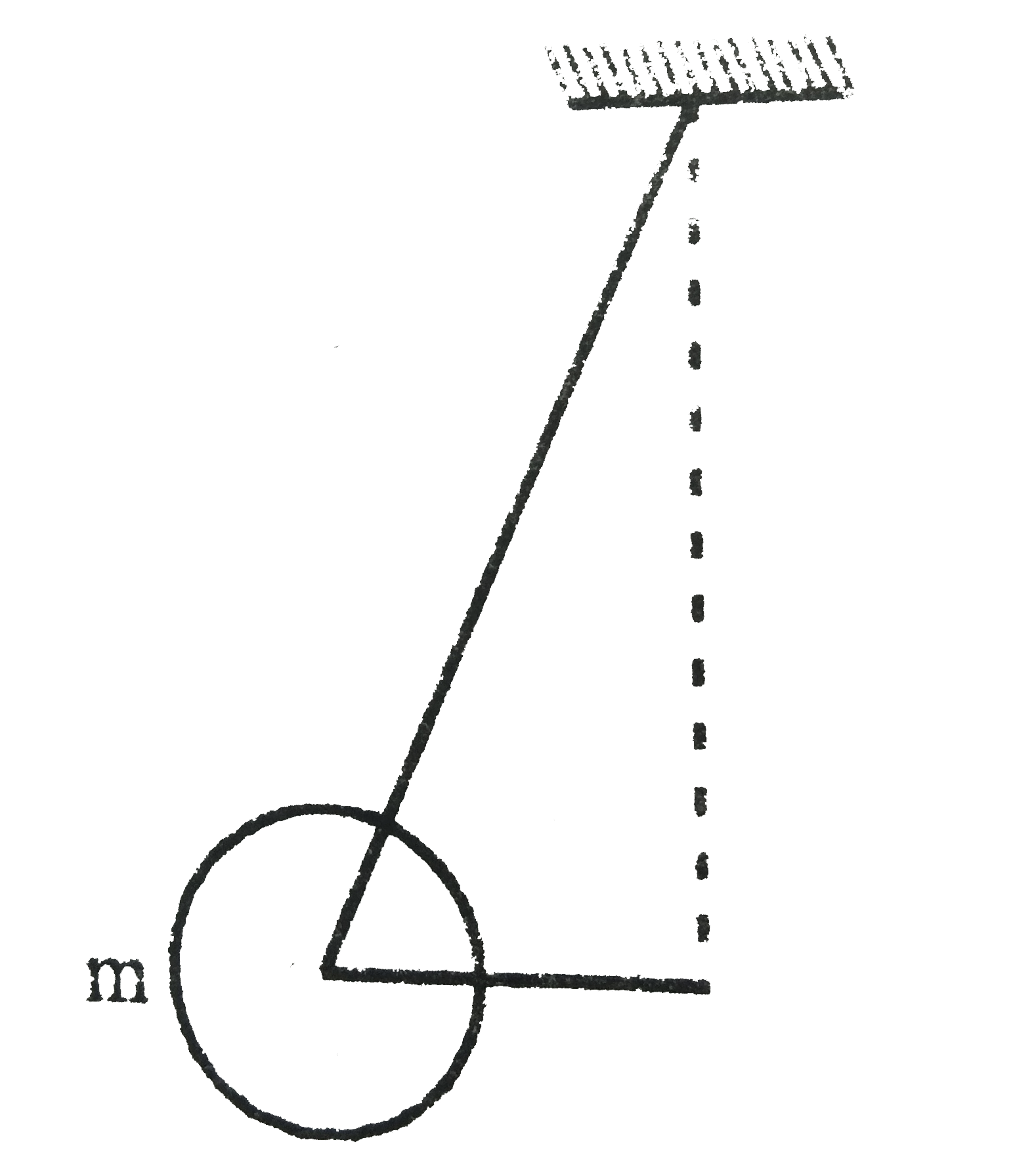 .
.
View SolutionA particle moves along a straight line and its velocity depends on time as v = 3t - t^2. Here, v is in m//s and t in second. Find (a) average velocity and (b) average speed for first five seconds.
View SolutionThe velocity 'v' of a particle moving along straight line is given in terms of time t as v=3(t^(2)-t) where t is in seconds and v is in m//s . The distance travelled by particle from t=0 to t=2 seconds is :
View SolutionThe velocity 'v' of a particle moving along straight line is given in terms of time t as v=3(t2−t) where t is in seconds and v is in m/s.
The displacement of aprticle from t=0 to t=2 seconds is :
View SolutionThe velocity 'v' of a particle moving along straight line is given in terms of time t as v=3(t2−t) where t is in seconds and v is in m/s.
The speed is minimum after t=0 second at instant of time
View SolutionThe speed(v) of a particle moving along a straight line is given by v=(t2+3t−4 where v is in m/s and t in seconds. Find time t at which the particle will momentarily come to rest.
View Solution2 मीटर त्रिज्या के पथ पर गतिमान एक कण की चाल समय के साथ समीकरण v=t2 के अनुसार बदलती है, जहां v मीटर/सेकण्ड तथा t सेकण्ड में है । t = 2 सेकण्ड पर ज्ञात कीजिये ---
त्रिज्या त्वरण
View Solution2 मीटर त्रिज्या के पथ पर गतिमान एक कण की चाल समय के साथ समीकरण v=t2 के अनुसार बदलती है, जहां v मीटर/सेकण्ड तथा t सेकण्ड में है । t = 2 सेकण्ड पर ज्ञात कीजिये ---
नेट त्वरण
View SolutionThe velocity v of a body moving along a straight line varies with time t as v=2t^(2)e^(-t) , where v is in m/s and t is in second. The acceleration of body is zero at t =
View Solutionएक सरल रेखा में गतिशील कण की चाल (v) समीकरण v=t2+3t−4 जहां v मीटर/सेकण्ड एवं t सेकण्ड में है द्वारा दी जाती है । वह समय ज्ञात कीजिए जिस पर कण क्षणिक रूप में विराम में आता है।
View Solutionएक सरल रेखा में गतिशील कण की चाल (v) एवं समय (t) समीकरण t2+100=2vt जहां v मीटर/सेकण्ड एवं t सेकण्ड में है द्वारा संबधित है। v के संभव धनात्मक मान ज्ञात कीजिए।
View SolutionThe velocity of an object moving in straight line path is given as a function of time by v=6t−3t2, where v is in ms−1, t is in s. The average velocity of the object between t=0 and t=2 second is
View SolutionA particle moves along a straight line and its velocity depends on time as v = 3t - t^2. Here, v is in m//s and t in second. Find (a) average velocity and (b) average speed for first five seconds.
View Solution
