A particle moves along a straight line and its velocity depends on time as v=3t−t2. Here, v is in m/s and t in second. Find
(a) average velocity and
(b) average speed for first five seconds.
The correct Answer is:A, B, C
(a) Average velocity=
Displacement /Time =∫50vdt5
=∫50(3t−t2)dt5
=−0.833m/s
(b) Velocity of particle=0 at t=3s
i.e, at 3s, particle changes its direction of
motion.
Average speed=(Total distance)/(Total time)
=((Distance from 0 to 3s)+(Distance from 3s to 5s))/Time
d0−3=∫30(3t−t2)dt=4.5m
d3−5=∫53(t2−3t)dt=8.67m
∴ Average speed =4.5+8.675
=2.63m/s
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - SCQ_TYPE41videos
KINEMATICS
- BOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - MCQ_TYPE23videos
KINEMATICS
- BOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - Comprehension7videos
KINEMATICS
- BOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises45videos
GRAVITATION
- BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE15videos
KINEMATICS 1
Similar Questions
A particle moves alo g a straight line and its velocity depends on time as v=6t−3t2 where 'v' is in m/sec and 't' is in sec. find average velocity and average speed forr first four seconds.
View Solutiona particle is moving in a straight line such that its velocity varies is given by v=10−2t, where v isin the first 8 second.
View Solution
Knowledge Check
- Question 1 - Select One or More
A particle moves along a straight line its velocity dipends on time as v=4t−t2. Then for first 5s:
AAverage velcotu is 25/3ms−1BAverage speed is 10ms−1.CAverage velcotu is 5/3ms−1DAcceleration is 4ms−2 at t=o - Question 2 - Select One
A particle is rotates in a circular path of radius 54m with varying speed v=4t2 . Here v is in m/s and t in second . Find angle between velocity and acceleration at t=3s .
Aθ=30∘Bθ=90∘Cθ=45∘DNone of the above - Question 3 - Select One
The motion of a particle along a straight line is described by the function x=(2t−3)2, where x is in metres and t is in seconds. Find
(a) the position, velocity and acceleration at t=2s.
(b) the velocity of the particle at the origin .A1 , 0 , 4B1 , 4 , 0C10 , 14 , −34D10 , −1 , 0
A particle is moving along x-axis. Its X-coordinate varies with time as, X=2t2+4t−6 Here, X is in meters and t in seconds. Find average velocity between the time interval t=0→t=2s.
View SolutionA particle in moving in a straight line such that its velocity is given by v=12t−3t2, where v is in m//s and t is in seconds. If at =0, the particle is at the origin, find the velocity at t=3s.
View SolutionVelocity-time graph of a particle moving in a straight line is shown in figure. In the time interval from t=0 to t=14s, find
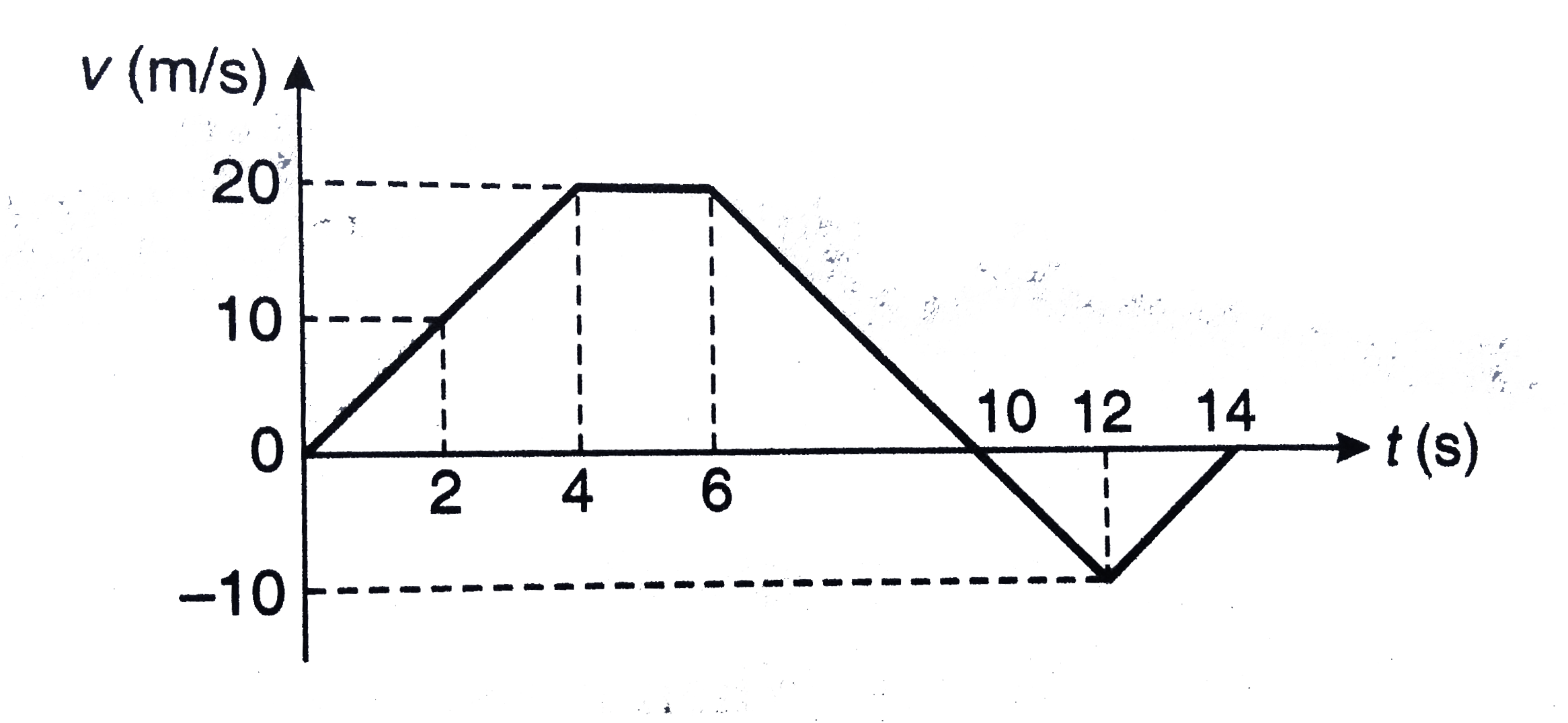
(a) average velocity and
(b) average speed of the particle.View SolutionThe position of a particle moving in a straight line is given by
x=3t3−18t2+36t
Here, x is in m and t in second. ThenView SolutionThe velocity 'v' of a particle moving along straight line is given in terms of time t as v=3(t2−t) where t is in seconds and v is in m/s.
The distance travelled by particle from t=0 to t=2seconds is :View Solution

