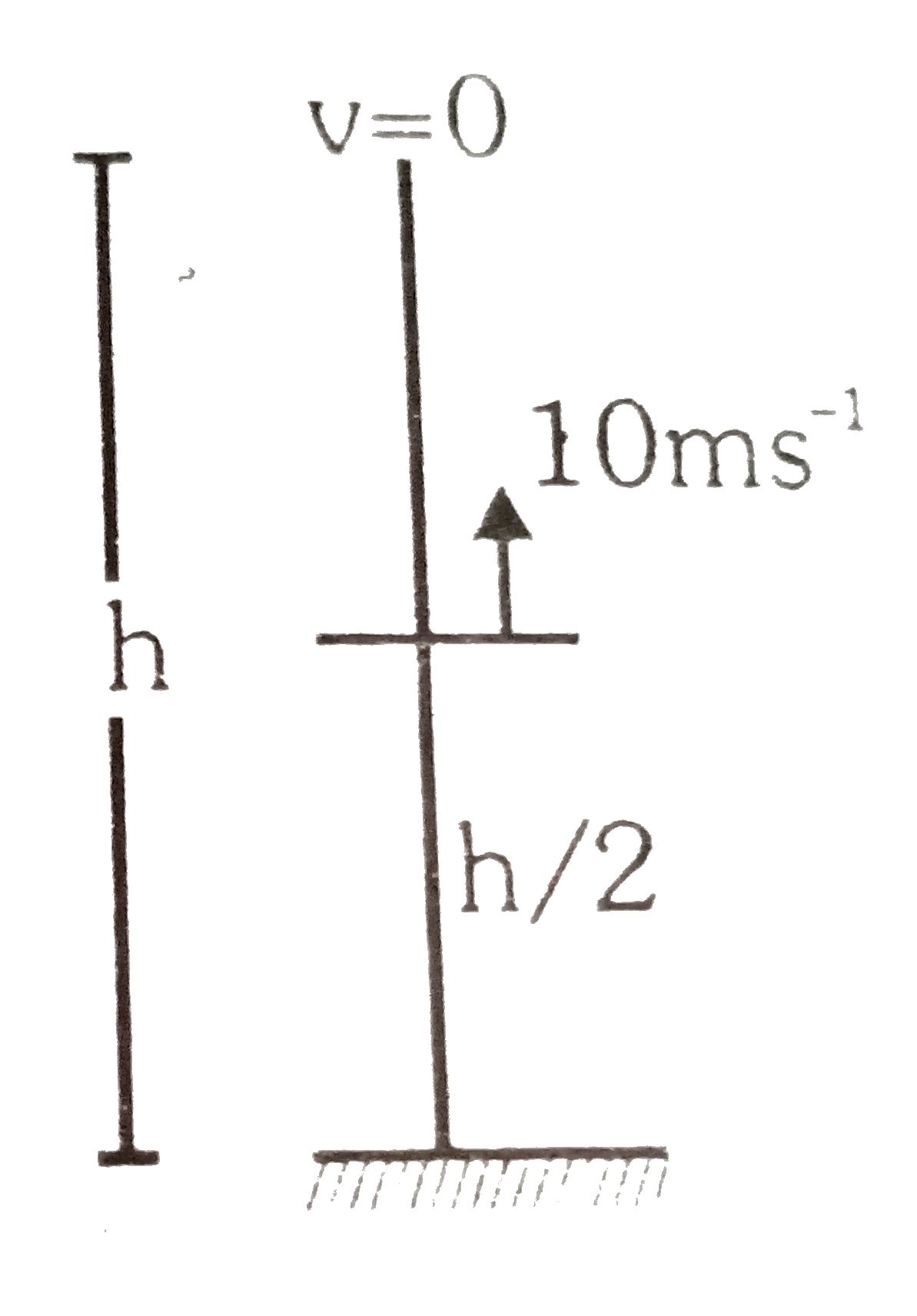
A stone is thrown vertically upwards. When stone is at a height half of its maximum height, its speed is 10ms−1 , then the maximum height attained by the stone is (g=10ms−2)Solution in Gujrati
The correct Answer is:(A)-r, (B)-p, (C)-r (D)-s
At t=0,v(0)=10m/s,t=0,v(6)=0
Change v(6)−v(0),Δv=0−10=−10m/s
Average acceleration
=charge in velocitytime=−106=−53m/s2
Average velocity =Displacementtime interval
Total displacement = Area of Δ's (with +ve or -ve)
=12×2×10−12×4×10=−10m (units)
∴ Average velocity =−106=−−53m/s
a(3)= slope of line which exist at t=0I0t=4
a=tanθ=−102=−5
Topper's Solved these Questions
- MOTION IN A PALNEBOOK - ALLEN CHAPTER - MOTION IN A PALNEEXERCISE - Assertion-Reason
20 Videos
- MOTION IN A PALNEBOOK - ALLEN CHAPTER - MOTION IN A PALNEEXERCISE - Comprehension#1
3 Videos
- MOTION IN A PALNEBOOK - ALLEN CHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-02
37 Videos
- KINEMATICS-2DBOOK - ALLEN CHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
47 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLEN CHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)
4 Videos
Similar Questions
An iron ball and a wooden ball of the same radius are released from a height ‘ h ’ in vacuum. The time taken by both of them to reach the ground is
View SolutionWhich of the following statements is incorrect?
(i) Average velocity is path length divided by time interval.
(ii) In general, speed is greater than the magnitude of the velocity.
(iii) Average velocity is diplacement divided by time interval.
(iv) The magnitude of average velocity is the average speed.
View SolutionThe distance x of a particle moving in one dimensions, under the action of a constant force is related to time t by the equation, t=√x+3, where x is in metres and t in seconds. Find the displacement of the particle when its velocity is zero.
View SolutionA particle is moving in xy-plane .At certain instant the components of its velocity and acceleration are as follows ux=3m/s,uy=4m/s,ax=2m/s2anday=1m/s2. The rate of change of speed at this moment is
View SolutionA piece of wire is bent in the shape of a parabola y=kx2 (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
View SolutionA stone is thrown vertically upwards. When stone is at a height half of its maximum height, its speed is 10 ms^-1 , then the maximum height attained by the stone is ( g= 10 ms^(-2) )
View SolutionA stone thrown upwards with speed u attains maximum height h. Ahother stone thrown upwards from the same point with speed 2u attains maximum height H. What is the relation between h and H?
View SolutionA stone is thrown vertically at a speed of 30ms−1 making an angle of 45∘ with the horizontal. What is the maximum height reached by the stone ? Take g=10ms−2.
View SolutionA particle thrown vertically upwards has velocity 10 ms^(-1) at half of its height, then maximum height attained by it is :
View SolutionA stone is thrown vertically at a speed of 30ms−1 taking an angle of 45∘ with the horizontal. What is the maximum height reached by the stone ? Take g=10ms−2.
View SolutionA stone is thrown vertically upwards with a velocity of 4.9 ms^(-1) . Calculate : the time taken to reach the maximum height.
View SolutionA stone is thrown vertically at a speed of 30 ms^(-1) taking an angle of 45^(@) with the horizontal. What is the maximum height reached by the stone ? Take g = 10 ms^(-2) .
View SolutionA stone is throuwn in a vertically upward direction with a velocity of 5ms−1. If the acceleration of the stone during its motion is 10ms−2 in the downword direction, what will be the height attained by the stone and how much time will it take to reach there ?
View SolutionA stone is thrown vertically upwards. When stone is at a height half of its maximum height, its speed is 10 ms^-1 , then the maximum height attained by the stone is ( g= 10 ms^(-2) )
View SolutionA stone is thrown vertically upwards. When stone is at a height half of its maximum height, its speed is 10ms−1 , then the maximum height attained by the stone is (g=10ms−2)
View Solution
