The resistance 4R,16R,64R....∞ are connected in series. Find their equivalent resistance. Solution in Gujrati
Take the physical system to be the gun and marble. Gravity and the normal force of the table act on the system. Both these forces are vertical. Since there are no horizontal external forces, the x component of the vector equation F=dPdt is 0=dPxdt According to equation (1), Px is conserved:
Px.initial=Px.final
 Let the initial time be prior to firing the gun. Then Px.initial=0, since the system is initially at rest. After the marble has left the muzzle, the gun recoils with some speed V1, and its final horizontal momentum is MV1, to the left. FInding the final velocity of the marble involves a subtle point, however. Physically, the marble's accelaration is due to the force of the gun, and the gun's recoil is due to the reaction force of the marble. The gun stops accelerating once the marble leaves the barrel, so that at the instant the marble and the gun part company, the gun has its final speed Vf. At that same instant the speed of the marble relative to the gun is v0. Hence, the final horizontal speed of the marble relative to the tablet is v0cosθ−Vf. By conservation of horizontal momentum, we therefore have
Let the initial time be prior to firing the gun. Then Px.initial=0, since the system is initially at rest. After the marble has left the muzzle, the gun recoils with some speed V1, and its final horizontal momentum is MV1, to the left. FInding the final velocity of the marble involves a subtle point, however. Physically, the marble's accelaration is due to the force of the gun, and the gun's recoil is due to the reaction force of the marble. The gun stops accelerating once the marble leaves the barrel, so that at the instant the marble and the gun part company, the gun has its final speed Vf. At that same instant the speed of the marble relative to the gun is v0. Hence, the final horizontal speed of the marble relative to the tablet is v0cosθ−Vf. By conservation of horizontal momentum, we therefore have
0=m(v0cosθ−Vf)−MVf
or Vf=mv0cosθM+m
By using conversation of momentum we found the final motion of the system in a few steps. To show the advantage of this method, let us repeat the problem using Newton's laws directly. Let v(t) be the velocity of marble at time t and let V(t) be the velocity of the gun. While the marble is going fired, it is acted on by the spring, by gravity, and by friction forces with the muzzle wall. Let the net force on the marble be f(t). The x equation of motion for the marble is
mdvxdt=fx(t) Formal integration of equation (3) gives
mvx(t)=mvz(0)+∫t0fxdt
The external forces are all vertical, and therefore the horizontal force fx on the marble is due entirely to the gun. By newton's third law, there is a reaction force- fx on the gun due to the marble. No other horizontal forces acts on the gun, and the horizontal equation of motion for the gun is therefore MdVxdt=−fx(t), which can be integrated to give
MVx(t)=MVx(0)−∫t0fxdt we can eliminate the integral by combining equation (4) and (5).
MVx(t)+mvx(t)=MVx(0)+mvz(0)
we have rediscovered that the horizontal component of momentum is conserved. What about the motion of the center of mass? Its horizontal velocity is
Rx(t)=MVx(t)+mvx(t)M+m Using equation (6), the numerator can be rewritten to give
Rx(t)=MVx(0)+mvx(0)M+m=0
SInce the system is initially at rest. Rx is constant, as we expect.
We did not include the small force of air friction. Would the center of mass remain at rest if we had included it? The essential step in our derivation of the law of conservation of momentum was to use Newton's third law. Thus, conservation of momentum appears to be natural consequence of newtonian mechanics. It has been found, however, that conservation of momentum holds true even in areas where newtonian mechanics proves inadequate, including the realms of quantum mechanics and relativity. In addition, conservation of momentumcan be generalized to apply to systems like the electromagnetic field, which possess momentum but not mass. For these reasons, conservation of momentum is generally regarded as being more fundamental than newtonian mechanics. From the point of view, Newton's thitd law is a simple consequance of conservation of momentum for interacting particles. For our present purposes it is purely a matter of taste whether we wish to regard Newton's third law or conservation of momentum as more fundamental.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - ALLEN CHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-III
26 Videos
- CURRENT ELECTRICITYBOOK - ALLEN CHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-IV A
32 Videos
- CIRCULAR MOTIONBOOK - ALLEN CHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (J-A)
6 Videos
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective
14 Videos
Similar Questions
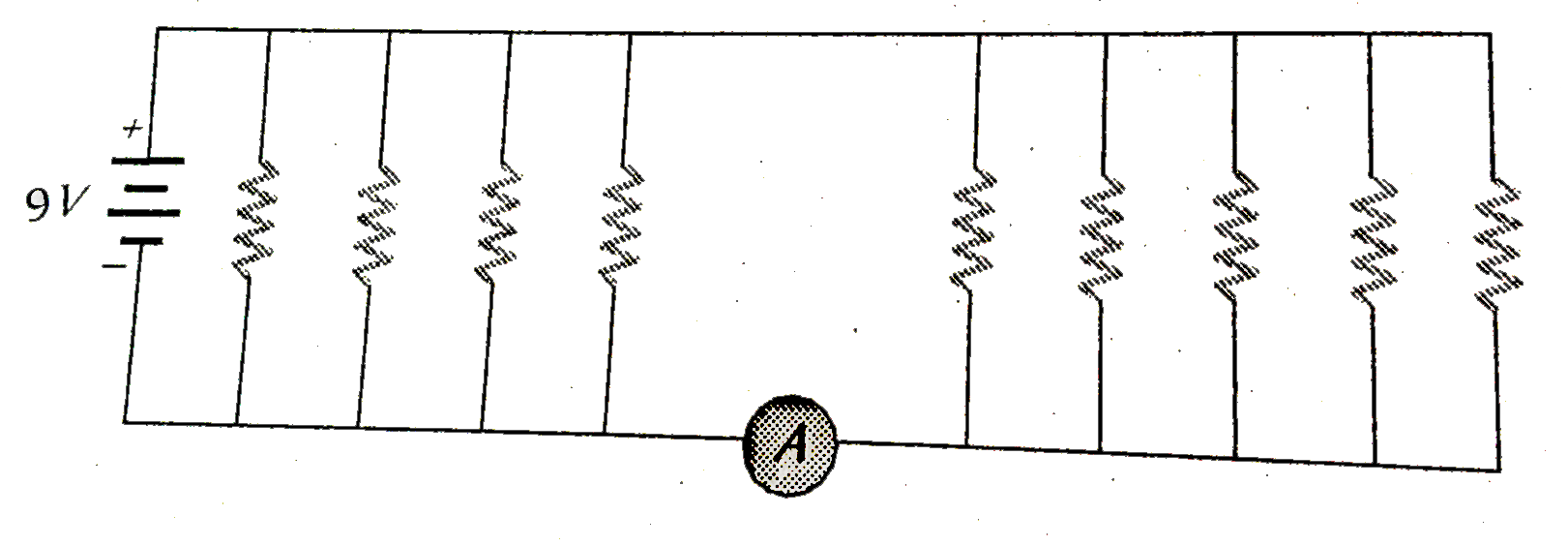
If each resistance in the figure is of 9Ω then reading of ammeter is
View SolutionBy a cell a current of 0.9 A flows through 2 ohm resistor and 0.3A through 7 ohm resistor. The internal resistance of the cell is
View SolutionA ball of mass (m)0.5kg is attached to the end of a string having length (L)0.5m. The ball is rotated on a horizontal circular path about vertical axis. The maximum tension that the string can bear is 324N. The maximum possible value of angular velocity of ball (radian/s) is -
 .
.
View SolutionA prism of refractive index n1 & another prism of reactive index n2 are stuck together without a gap as shown in the figure.The angle of the prisms are as shown. n1&n2depend onλ,the wavelength of light according to n1=1.20+10.8×104λ2&n2=1.45+1.80×104λ2 where λ is in nm.

(i)Calculate the wavelength λ0for which rays incident at any angle on the interfaceBCpass through without bending at that interface.
(ii) for light of wavelength λ0,find the angle of incidencei on faceACsuch that the deviation produced by the combination of prism is minimum.
View SolutionThe equivalent resistance of two resistor connected in series is 6Ω and their equivalent resistance is 43Ω. What are the values of resistances ?
View SolutionResistance R,2R,4R,8R ...... ∞ are connected in parallel. What is their resutlant resistance will be
View Solutionयदि 2Ω प्रतिरोध के 2 तार श्रेणीक्रम में जुड़े हों, तो उनका समतुल्य प्रतिरोध होगा
View Solutionसमान प्रतिरोध 4r वाले चार प्रतिरोधकों को किस प्रकार संयोजित किया जावे कि उनका तुल्य प्रतिरोध 10r हो, प्रत्येक स्थिति के संयोजन का चित्र बनाकर तुल्य प्रतिरोध प्राप्त कीजिए।
View Solutionसमान प्रतिरोध 4r वाले चार प्रतिरोधकों को किस प्रकार संयोजित किया जावे कि उनका तुल्य प्रतिरोध 16r3 हो, प्रत्येक स्थिति के संयोजन का चित्र बनाकर तुल्य प्रतिरोध प्राप्त कीजिए।
View SolutionWhen two resistances connected in series and parallel their equivalent resistances are 15Omega and (56)/(15)Omega respectively. Find the individual resistances.
View SolutionFind the equivalent resistance of the two resistors connected in parallel series.
View Solutionप्रतिरोध R, 2R, 4R, 8R…∞ समान्तर क्रम में जुड़े हुए है। उनका तुल्य प्रतिरोध कितना होगा?
View SolutionFind the equivalent of resistances of the individual resistance connected in series?
View SolutionThe equivalent resistance of two resistor connected in series is 6 Omega and their equivalent resistance is (4)/(3)Omega . What are the values of resistances ?
View SolutionKirchhOFf's Laws||Series and Parallel Connections OF Resistances||Equivalent Resistance||Junction Potential
View SolutionWhen two resistances are connected in series, the equivalent resistance is _______.
View Solution
