A particle is projected up an inclines plane. Plane is inclined at an angle θ with horizontal and particle is projected at an angle α with horizontal. If particle strikes the plane horizontally prove that tanα=2tanθSolution in Gujrati
We know time of flight
T=2usin(α+θ)gcosθ
Considering vertical motion
u=vsinα
a=−g
v=θ
∴T=usinαg=2usin(α−θ)gcosθ
sinαcosθ=2sinαcosθ−2cosαsinθ
2cosαsinθ=sinαcosθ
2tanθ=tanα
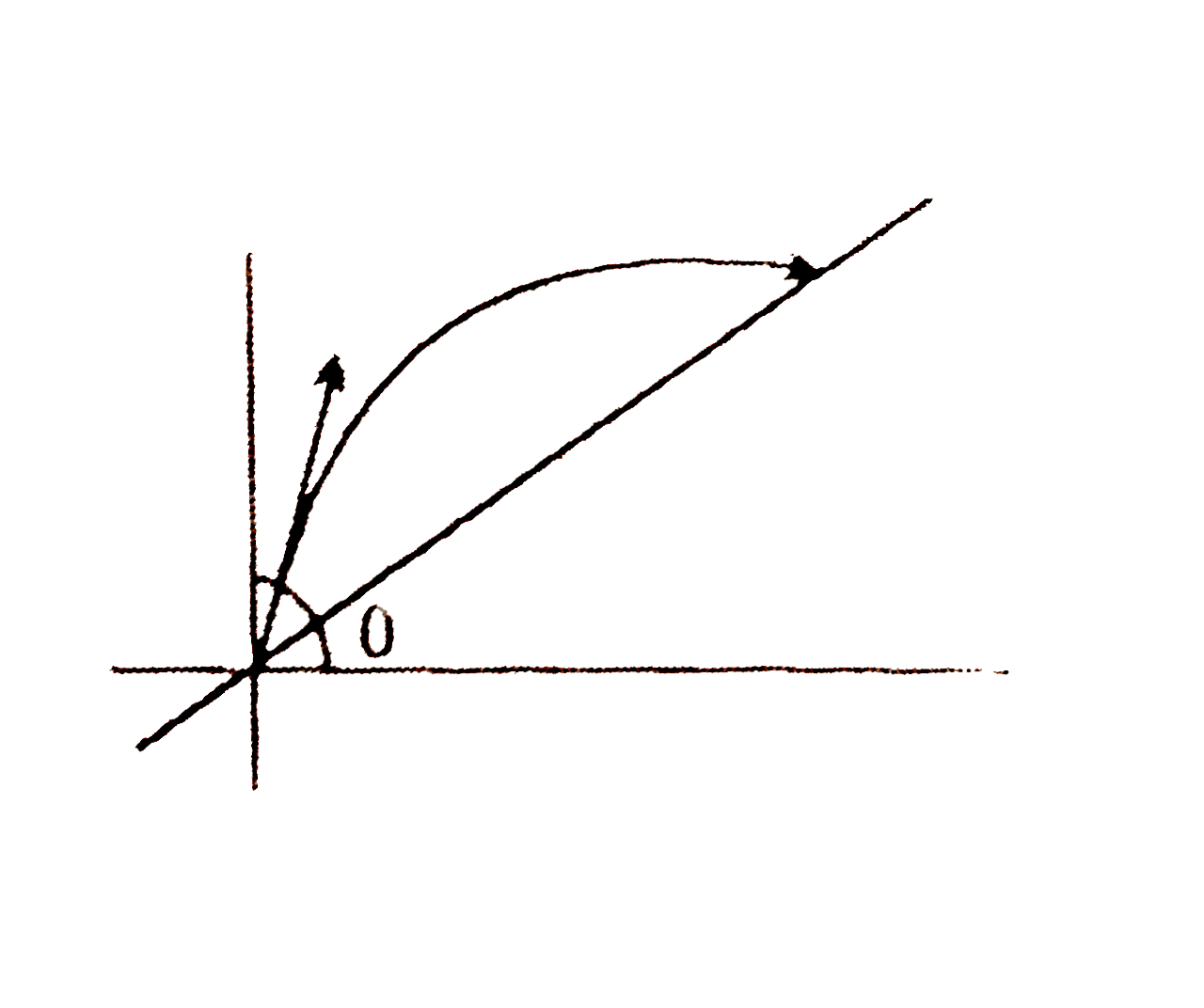
Topper's Solved these Questions
- KINEMATICS-2DBOOK - ALLEN CHAPTER - KINEMATICS-2DEXERCISE - Exercise (S-1)
30 Videos
- KINEMATICS-2DBOOK - ALLEN CHAPTER - KINEMATICS-2DEXERCISE - Exercise (S-2)
14 Videos
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
- MOTION IN A PALNEBOOK - ALLEN CHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE
28 Videos
Similar Questions
The vertical height y and horizontal distance x of a projectile on a certain planet are given by x=(3t)m,y=(4t−6t2) m where t is in seconds, Find the speed of projection (in m/s).
View SolutionA particle travels so that its acceleration is given by →a=5costˆi−3sintˆj. If the particle is located at (−3,2) at time t=0 and is moving with a velocity given by (−3ˆi+2ˆj). Find
(i) The velocity [→v=∫→a.dt] at time t and
(ii) The position vector [→r=∫→v.dt] of the particle at time t(t>0).
View SolutionAssertion : The difference in the value of acceleration due to gravity at pole and equator is proportional to square of angular velocity of earth.
Reason : the value of acceleration due to gravity is minimum at the equator and maximum at the pole.
View SolutionA particle thrown over a triangle from one end of a horizontal base falls on the other end of the base after grazing the vertex. If αandβ are the base angles of triangle and angle of projection is θ, then prove that (tanθ=tanα+tanβ)
View SolutionAn particle is projected with velocity u on an inclined plane at an angle theta with the plane. If the particle lands on the plane at right its time of flight is (u cosec theta)/(2 g) . Find the angle of inclination of the plane with horizontal.
View SolutionA particle is projected horizontally with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane ?

View SolutionA particle is projected horizontal with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane?
View SolutionA particle is projected with a certain velocity at an angle alpha above the horizontal from the foot of an inclined plane of inclination 30^(@) . If the particle strikes the plane normally then alpha is equal to
View SolutionA particle is projected at an angle α with the horizontal from the foot of an inclined plane making an angle β with horizontal . Which of the following expressions holds good if the particle strikes the inclined plane normally?
View SolutionA particle projected horizontally from the top of an inclined plane inclined at an angle theta with the horizontal with velocity u. What is the distance along the plane from the point of projection at which the projectile strikes the inclined plane ?
View SolutionA particle is projected horizontally with a speed ''u'' rom the top of plane incline at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane ?
View SolutionA particle is projected horizontally with a speed ''u'' rom the top of plane incline at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane ?
View SolutionA particle is projected horizontally with a speed ''u'' rom the top of plane incline at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane ?
View SolutionA particle is projected horizontally with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane ?

View SolutionA particle is projected horizontally with a speed "u" from the top of plane incline at an angle ..θ.. with the horizontal. How far from the point of projection will the particle strike the plane ?
View SolutionA particle is projected horizontally with a speed "u" from the top of plane incline at an angle ..θ.. with the horizontal. How far from the point of projection will the particle strike the plane ?
View Solution
