Velocity of the boat with respect to river is 10m/s. From point A it is steered in the direction shown. Where will it reach on the opposite bank ?
 Solution in Gujrati
Solution in Gujrati
The correct Answer is:30 m upstream
Step by step video & image solution for Velocity of the boat with respect to river is 10m/s. From point A it is steered in the direction shown. Where will it reach on the opposite bank ? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINEMATICS-2DBOOK - ALLEN CHAPTER - KINEMATICS-2DEXERCISE - Exercise (S-2)
14 Videos
- KINEMATICS-2DBOOK - ALLEN CHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-1)
40 Videos
- KINEMATICS-2DBOOK - ALLEN CHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
47 Videos
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
- MOTION IN A PALNEBOOK - ALLEN CHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE
28 Videos
Similar Questions
A particle travels so that its acceleration is given by →a=5costˆi−3sintˆj. If the particle is located at (−3,2) at time t=0 and is moving with a velocity given by (−3ˆi+2ˆj). Find
(i) The velocity [→v=∫→a.dt] at time t and
(ii) The position vector [→r=∫→v.dt] of the particle at time t(t>0).
View SolutionA particle is projected form a horizontal plane (x−z plane) such that its velocity vector at time t is gives by →V=aˆi+(b−ct)ˆj. Its range on the horizontal plane is given by
View SolutionA particle is moving in xy-plane .At certain instant the components of its velocity and acceleration are as follows ux=3m/s,uy=4m/s,ax=2m/s2anday=1m/s2. The rate of change of speed at this moment is
View SolutionAssertion : The difference in the value of acceleration due to gravity at pole and equator is proportional to square of angular velocity of earth.
Reason : the value of acceleration due to gravity is minimum at the equator and maximum at the pole.
View SolutionA particle thrown over a triangle from one end of a horizontal base falls on the other end of the base after grazing the vertex. If αandβ are the base angles of triangle and angle of projection is θ, then prove that (tanθ=tanα+tanβ)
View SolutionA river 400 m wide is flowing at a rate of 2.0 m//s. A boat is sailing at a velocity of 10.0 m//s with respect to the water In a direction perpendicular to the river. (a) Find the time taken by the boat to reach the opposite bank. (b) How far from the point directly opposite to the starting point does the boat reach the opposite bank?
View SolutionA 400−m wide river is flowing at a rate of 2.0ms−1. A boat is sailing with a velocity of 10ms−1 with respect to the water, in a direction perpendicular to the river.
(a) Find the time taken by the boat to reach the opposite bank.
(b) How far from the point directly opposite to the starting point does the boat reach the opposite bank ?
( c) In what direction does the boat actually move ?
View SolutionA river 500m wide is flowing at a rate of 4 m//s. A boat is sailing at a velocity of 10 m//s with respect to the water, in a direction perpendicular to the river. The time taken by the boat to reach the opposite bank
View SolutionA motor boat is to reach at a point 30∘ upstream on the outer side of a river flowing with velocity 5ms−1. The velocity of motor boat with respect to water is 5(√3)ms−1. The driver should steer the boat at an angle.
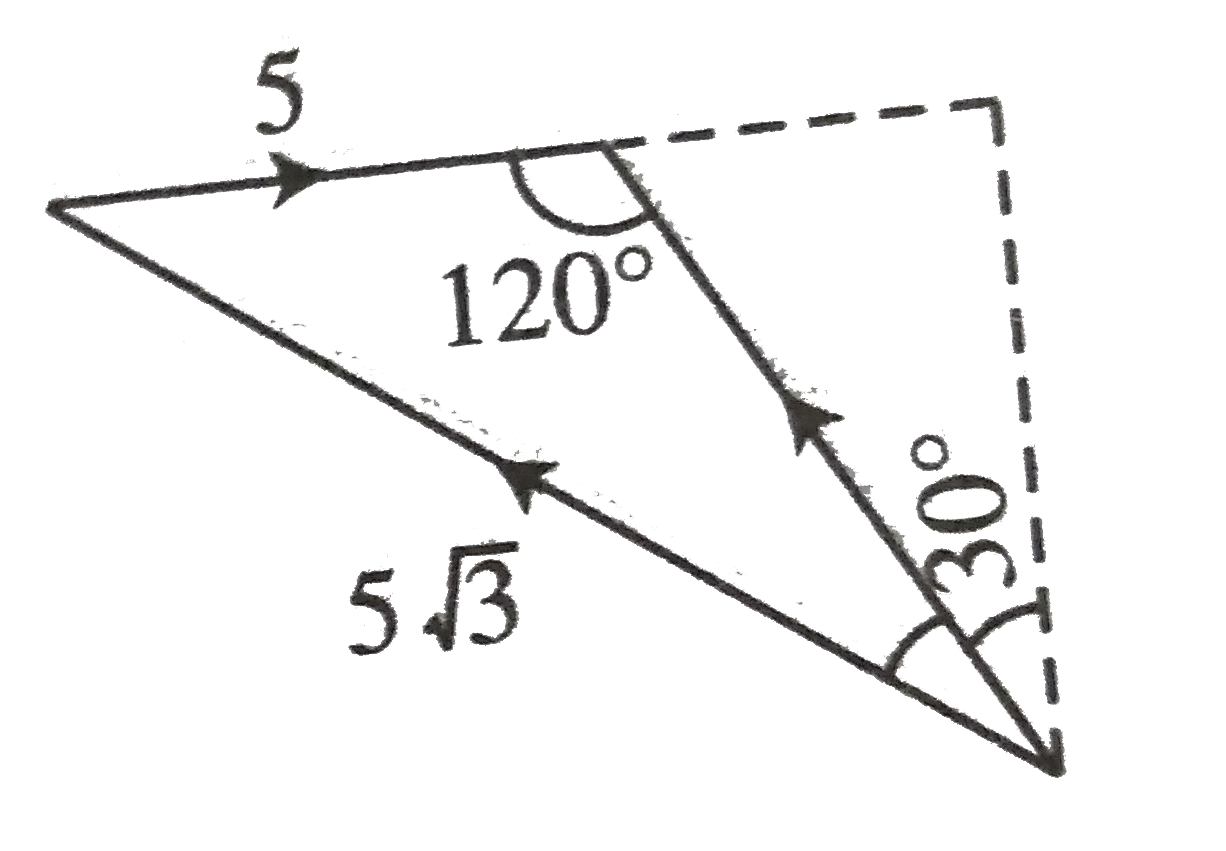
View SolutionVelocity of a boat relative to river current and river current velocity are equal in magnitude. Starting from point A on the southern bank, the boatman wants to reach a point B on the nothern bank in north - east from A . In which direction he has to steer the boat?
View SolutionVelocity of the boat with respect to river is 10 m/s. From point A it is steered in the direction shown to reach point C. Find the time of the trip and distance between B and C

View SolutionA river 60m wide is flowing at a rate of 4m/s .A boat is sailing at a velocity of 20 m/s with respect to the river in a direction making an angle 37∘ with the direction of river flow.Find time taken by the boat in seconds to reach the opposite bank. (A) 2 (B) 3 (C) √6 (D) 5
View SolutionA boat was steered over a flowing river in such a way that it reached the opposite bank following the shortest path. Time required in this case was double the time the boat would have taken to cross the river if there was no river current. If the velocity of the boat was 2 m *s^(-1) , what was the velocity of the current?
View SolutionA 400m wide river is flowing at a rate of 2.0ms−1. A boat is sailing with a velocity of 10ms−1 with respect to the water, in a direction perpendicular to the river.
(a) Find the time taken by the boat to reach the opposite bank.
(b) How far from the point directly opposite to the starting point does the boat reach the opposite bank ?
( c) In what direction does the boat actually move ?
View Solutionएक नाव को धारा को प्रतिकूल दिशा में 30∘ (अभिलम्ब से) दूसरी ओर स्थित बिन्दु पर पहुचना है। नदी 5m/s के वेग से बह रही है। नाव का जल के सापेक्ष वेग 5√3m/s है। नाविक को किसी कोण पर नाव चलानी होगा।
View SolutionA motor boat is to reach at a point 30^@ upstream on other side of the river flowing with velocity 5m//s The velocity of motor boat with respect to water is 5sqrt3 m//s . At what angle the driver should steer the boat ?
View Solution
