A body is projected up with a speed v0 along the line of greatest slope of an inclined plane of angle of inclination β. If the body collides elastically perpendicular to the inclined plane, find the time after which the body passes through its point of projection.
To solve the problem, we need to analyze the motion of a body projected up an inclined plane and determine the time after which it returns to its point of projection after an elastic collision. Here’s a step-by-step solution:
Step 1: Understand the Motion Components
The body is projected with an initial speed v0 along the inclined plane, which makes an angle β with the horizontal. We need to resolve the motion into two components: parallel to the inclined plane (x-direction) and perpendicular to the inclined plane (y-direction).
Step 2: Resolve Initial Velocity
- The component of the initial velocity along the inclined plane (x-direction) is:
v0x=v0cos(β)
- The component of the initial velocity perpendicular to the inclined plane (y-direction) is:
v0y=v0sin(β)
Step 3: Apply Equations of Motion in the x-direction
Using the equation of motion:
vx=ux+axt
where vx=0 (final velocity at the peak), ux=v0cos(β), and ax=−gsin(β) (acceleration due to gravity along the incline):
0=v0cos(β)−gsin(β)t
From this, we can solve for time t to reach the highest point:
t=v0cos(β)gsin(β)
Step 4: Apply Equations of Motion in the y-direction
Using the equation of motion for vertical displacement (which is zero when it returns to the same height):
sy=uyt+12ayt2
where sy=0, uy=v0sin(β), and ay=−gcos(β):
0=v0sin(β)t−12gcos(β)t2
Factoring out t:
t(v0sin(β)−12gcos(β)t)=0
This gives us two solutions: t=0 (initial point) or:
t=2v0sin(β)gcos(β)
Step 5: Equate the Times
Since the time to reach the highest point and the time to return to the original height must be equal for the body to pass through its point of projection after the elastic collision, we equate the two expressions for time:
v0cos(β)gsin(β)=2v0sin(β)gcos(β)
Step 6: Solve for Total Time
The total time after which the body passes through its point of projection (considering the elastic collision) is:
T=2×v0cos(β)gsin(β)
Substituting the values gives:
T=4v0sin(β)gcos(β)
Final Answer
The total time after which the body passes through its point of projection is:
T=4v0g√1+3sin2(β)
The body is projected with an initial speed v0 along the inclined plane, which makes an angle β with the horizontal. We need to resolve the motion into two components: parallel to the inclined plane (x-direction) and perpendicular to the inclined plane (y-direction).
- The component of the initial velocity along the inclined plane (x-direction) is:
v0x=v0cos(β)
- The component of the initial velocity perpendicular to the inclined plane (y-direction) is:
v0y=v0sin(β)
Using the equation of motion:
vx=ux+axt
where vx=0 (final velocity at the peak), ux=v0cos(β), and ax=−gsin(β) (acceleration due to gravity along the incline):
0=v0cos(β)−gsin(β)t
From this, we can solve for time t to reach the highest point:
t=v0cos(β)gsin(β)
Using the equation of motion for vertical displacement (which is zero when it returns to the same height):
sy=uyt+12ayt2
where sy=0, uy=v0sin(β), and ay=−gcos(β):
0=v0sin(β)t−12gcos(β)t2
Factoring out t:
t(v0sin(β)−12gcos(β)t)=0
This gives us two solutions: t=0 (initial point) or:
t=2v0sin(β)gcos(β)
Since the time to reach the highest point and the time to return to the original height must be equal for the body to pass through its point of projection after the elastic collision, we equate the two expressions for time:
v0cos(β)gsin(β)=2v0sin(β)gcos(β)
The total time after which the body passes through its point of projection (considering the elastic collision) is:
T=2×v0cos(β)gsin(β)
Substituting the values gives:
T=4v0sin(β)gcos(β)
The total time after which the body passes through its point of projection is:
T=4v0g√1+3sin2(β)
Topper's Solved these Questions
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Solved Examples
7 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.1
15 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
Similar Questions
A block is projected up along the line of greatest slope of an inclined plane of angle of inclination 0(<ϕ) where ϕ= angle of friction. Which of the following friction time graph is CORRECT ?
View SolutionA particle projected with velcoity v0 strikes at right α plane through the point of projection .
View SolutionA particle is projected along the line of greatest slope up a rough plane inclined at an angle of 45∘ with the horizontal. If the coefficient of friction is 1/2 . Their retardation is:
View SolutionA particle is projected along the line of greatest slope up a rough plane inclined at an angle of 45∘ with the horizontal. If the coefficient of friction is 1/2 . Their retardation is:
View SolutionA projectile is projected with speed u at an angle of 60∘ with horizontal from the foot of an inclined plane. If the projectile hits the inclined plane horizontally, the range on inclined plane will be.
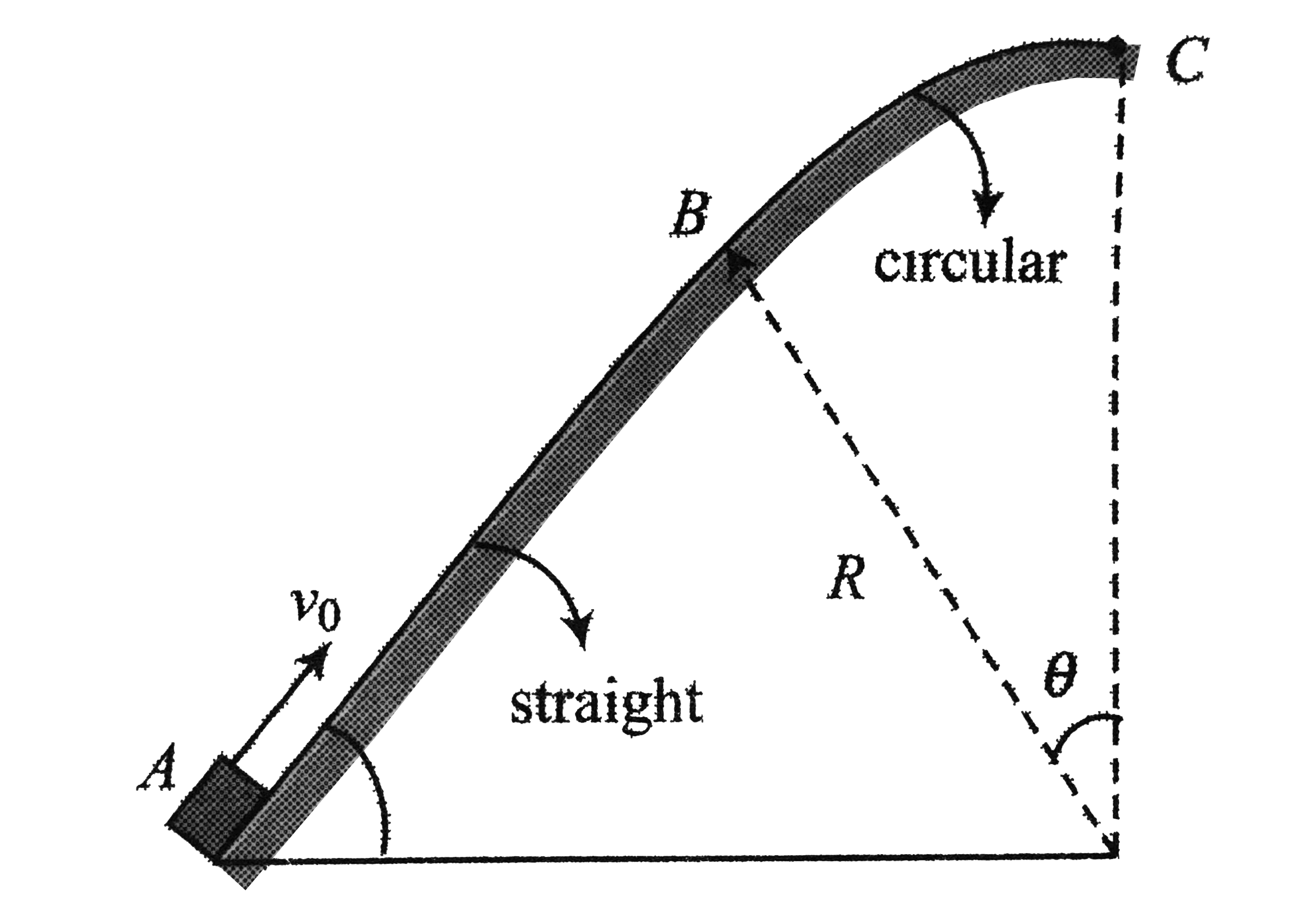
View SolutionA block of mass m is projected up with a velocity v0 along an inclined plane of angle of inclination θ=37∘. The coefficient of friction between the inclined plane AB and blocks is μ(=tanθ). Find the values of v0 so that the block moves in a circular path from B to C.
View SolutionA body is projected upwards with a velocity u. It passes through a certain point above the ground after t1, Find the time after which the body passes through the same point during the journey.
View SolutionA ball is projected horizontally with a speed v from the top of the plane inclined at an angle 45∘ with the horizontal. How far from the point of projection will the ball strikes the plane?
View SolutionA particle is projected on an inclined plane with a speed u as shown in (Fig. 5.61). Find the range of the particle on the inclined plane.
 .
.
View SolutionA particle is projected horizontally with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane ?

View Solution
