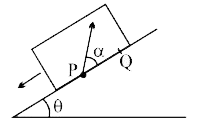
A large , heavy box is sliding without friction down a smooth plane of inclination θ . From a point P on the bottom of the box , a particle is projected inside the box . The initial speed of the particle with respect to the box is u , and the direction of projection makes an angle α with the bottom as shown in Figure .
(a) Find the distance along the bottom of the box between the point of projection p and the point Q where the particle lands . ( Assume that the particle does not hit any other surface of the box . Neglect air resistance .)
(b) If the horizontal displacement of the particle as seen by an observer on the ground is zero , find the speed of the box with respect to the ground at the instant when particle was projected .
 Solution in Gujrati
Solution in Gujrati
The correct Answer is:(i) u2sin2αgcosθ (ii) v=ucos(α+0)cosθ
Step by step video & image solution for A large , heavy box is sliding without friction down a smooth plane of inclination theta . From a point P on the bottom of the box , a particle is projected inside the box . The initial speed of the particle with respect to the box is u , and the direction of projection makes an angle alpha with the bottom as shown in Figure . (a) Find the distance along the bottom of the box between the point of projection p and the point Q where the particle lands . ( Assume that the particle does not hit any other surface of the box . Neglect air resistance .) (b) If the horizontal displacement of the particle as seen by an observer on the ground is zero , find the speed of the box with respect to the ground at the instant when particle was projected . by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINEMATICS-2DBOOK - ALLEN CHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-1)
40 Videos
- KINEMATICS-2DBOOK - ALLEN CHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
47 Videos
- KINEMATICS-2DBOOK - ALLEN CHAPTER - KINEMATICS-2DEXERCISE - Exercise (S-1)
30 Videos
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
- MOTION IN A PALNEBOOK - ALLEN CHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE
28 Videos
Similar Questions
A particle is projected form a horizontal plane (x−z plane) such that its velocity vector at time t is gives by →V=aˆi+(b−ct)ˆj. Its range on the horizontal plane is given by
View SolutionA particle is moving in xy-plane .At certain instant the components of its velocity and acceleration are as follows ux=3m/s,uy=4m/s,ax=2m/s2anday=1m/s2. The rate of change of speed at this moment is
View SolutionThe vertical height y and horizontal distance x of a projectile on a certain planet are given by x=(3t)m,y=(4t−6t2) m where t is in seconds, Find the speed of projection (in m/s).
View SolutionAssertion : The difference in the value of acceleration due to gravity at pole and equator is proportional to square of angular velocity of earth.
Reason : the value of acceleration due to gravity is minimum at the equator and maximum at the pole.
View SolutionA particle thrown over a triangle from one end of a horizontal base falls on the other end of the base after grazing the vertex. If αandβ are the base angles of triangle and angle of projection is θ, then prove that (tanθ=tanα+tanβ)
View SolutionA large , heavy box is sliding without friction down a smooth plane of inclination θ . From a point P on the bottom of the box , a particle is projected inside the box . The initial speed of the particle with respect to the box is u , and the direction of projection makes an angle α with the bottom as shown in Figure .
(a) Find the distance along the bottom of the box between the point of projection p and the point Q where the particle lands . ( Assume that the particle does not hit any other surface of the box . Neglect air resistance .)
(b) If the horizontal displacement of the particle as seen by an observer on the ground is zero , find the speed of the box with respect to the ground at the instant when particle was projected .

View SolutionA box is falling freely. Inside the box, a particle is projected with some velocity v with respect to the box at an angle theta as shown in the figure. Assertion (A) : The path of the particle with respect to an oberver sitting in the box will be a straight line. Reasoning (R ) : The acceleration of particle with respect to the box is zero. Then,
View SolutionA box is failing freely. Inside the box, a particle is projected with some velocity v with respect to the box at an angle θ as shown in the figure.

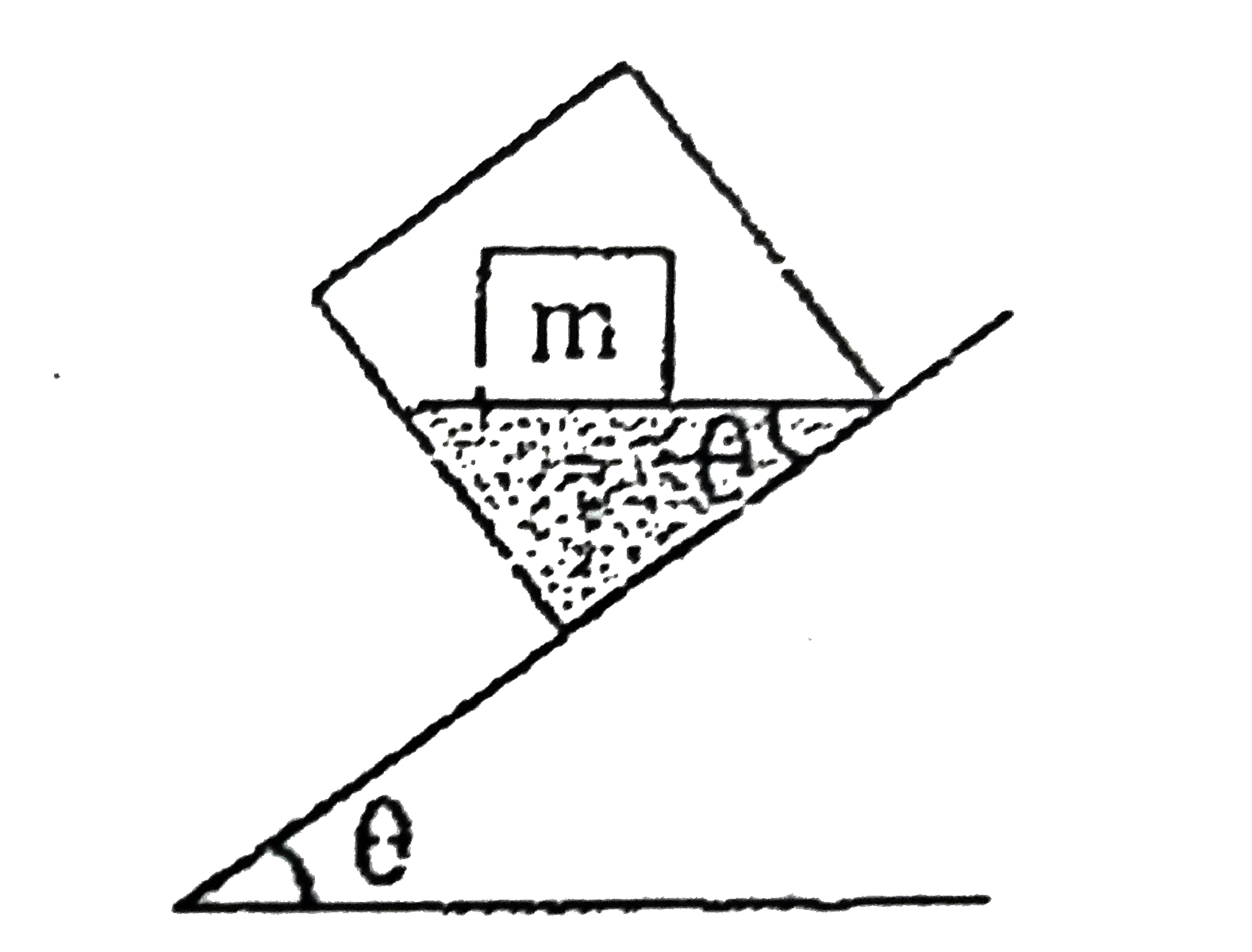
View SolutionA very heavy box is kept on a frictionless incline plane inclined at an angle θ from the horizontal. Box is having an another frictionless incline plane, inclined plane as shown in the figure. A block of mass m is kept on this inclined plane inside the box. Acceleration of block w.r.t. box is
View SolutionA large box is moving on a horizontal floor with constant acceleration a=g. A particle is projected inside box with velocity u and angle theta with horizontal from box frame. For the given u, the value of theta for which horizontal range inside he box will be maximum is
View SolutionA rectangular box lies on a rough inclined surface. The coefficient of friction between the surface and the box is (μ) Let the mass of the box be m.
At what angle of inclination θ of the plane to the horizontal will the box just start to slide down the plane ?
View SolutionA box is lying on an inclined plane if the box slides when the angle of inclination is 60^(@) then the coefficient of static friction of the box and the plane is?
View SolutionA wooden box is lying on an inclined plane. What is the coefficient of friction if the box starts sliding when the angle of inclination is 45∘
View SolutionA large , heavy box is sliding without friction down a smooth plane of inclination θ . From a point P on the bottom of the box , a particle is projected inside the box . The initial speed of the particle with respect to the box is u , and the direction of projection makes an angle α with the bottom as shown in Figure .
(a) Find the distance along the bottom of the box between the point of projection p and the point Q where the particle lands . ( Assume that the particle does not hit any other surface of the box . Neglect air resistance .)
(b) If the horizontal displacement of the particle as seen by an observer on the ground is zero , find the speed of the box with respect to the ground at the instant when particle was projected .

View Solutionθ नत कोण वाले घर्षण रहित तल पर एक बड़ा भारी बॉक्स फिसल रहा है। बाक्स के तल पर स्थित बिन्दु P से बॉक्स के भीतर एक कण प्रक्षेपित किया जाता है। कण की बॉक्स के सापेक्ष प्रारम्भिक वेग u है तथा प्रक्षेपण की दिशा तल से चित्रानुसार α है।
(a) बॉक्स में नत के अनुदशि प्रक्षेपण बिन्दु P से Q की दूरी ज्ञात करो जहाँ कण टकराता है। (कण बॉक्स में और कही नही टकराता एवं वायु प्रतिरोध नगण्य है
View Solution
