A rectangular box is sliding on a smooth inclined plane of inclination α as shown in the figure. At t = 0, the box starts to move on the inclined plane. A bolt starts to fall from point A. Find the time after which bolt strikes the bottom surface of the box.
The correct Answer is:C
To solve the problem of determining the time after which the bolt strikes the bottom surface of the box sliding down an inclined plane, we can follow these steps:
Step 1: Understand the Motion of the Box and the Bolt
At time t=0, the box starts moving down the inclined plane with an angle of inclination α. Simultaneously, a bolt starts to fall from point A. The box and the bolt will have the same horizontal acceleration due to the smooth incline.
Step 2: Identify the Acceleration of the Bolt
The acceleration of the box down the incline is given by the component of gravitational acceleration acting along the incline:
abox=gsinα
However, since the bolt falls vertically, its vertical acceleration is simply g. The bolt will also have a horizontal component of motion due to the incline:
abolt=gcosα
Step 3: Set Up the Equation of Motion for the Bolt
The bolt starts falling from rest, so its initial velocity u=0. The distance s that the bolt falls vertically is equal to the distance l that the box slides down the incline. We can use the equation of motion:
s=ut+12at2
Substituting the values:
l=0+12(gcosα)t2
Step 4: Rearrange the Equation to Solve for Time t
Rearranging the equation gives:
l=12gcosα⋅t2
Multiplying both sides by 2:
2l=gcosα⋅t2
Now, solving for t2:
t2=2lgcosα
Taking the square root:
t=√2lgcosα
Step 5: Conclusion
The time after which the bolt strikes the bottom surface of the box is given by:
t=√2lgcosα
At time t=0, the box starts moving down the inclined plane with an angle of inclination α. Simultaneously, a bolt starts to fall from point A. The box and the bolt will have the same horizontal acceleration due to the smooth incline.
The acceleration of the box down the incline is given by the component of gravitational acceleration acting along the incline:
abox=gsinα
However, since the bolt falls vertically, its vertical acceleration is simply g. The bolt will also have a horizontal component of motion due to the incline:
abolt=gcosα
The bolt starts falling from rest, so its initial velocity u=0. The distance s that the bolt falls vertically is equal to the distance l that the box slides down the incline. We can use the equation of motion:
s=ut+12at2
Substituting the values:
l=0+12(gcosα)t2
Rearranging the equation gives:
l=12gcosα⋅t2
Multiplying both sides by 2:
2l=gcosα⋅t2
Now, solving for t2:
t2=2lgcosα
Taking the square root:
t=√2lgcosα
The time after which the bolt strikes the bottom surface of the box is given by:
t=√2lgcosα
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Assignement section -C Objective (More than one option is correct)
7 Videos
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Assignement section -D (Linked Comprehension)
12 Videos
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Assignement section -A Objective (one option is correct)
50 Videos
- MOCK_TEST_17BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOCK_TEST_17EXERCISE - Example
15 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - D)
15 Videos
Similar Questions
A rod AB is placed on smooth inclined plane as shown in the figure. At the instant which is shown in the figure, the angular velocity of the rod is
View SolutionA particle slides down a smooth inclined plane of elevation θ fixed in an elevator going up with an acceleration a0. The base of the incline has a length L. Find the time taken by the particle to reach the bottom.
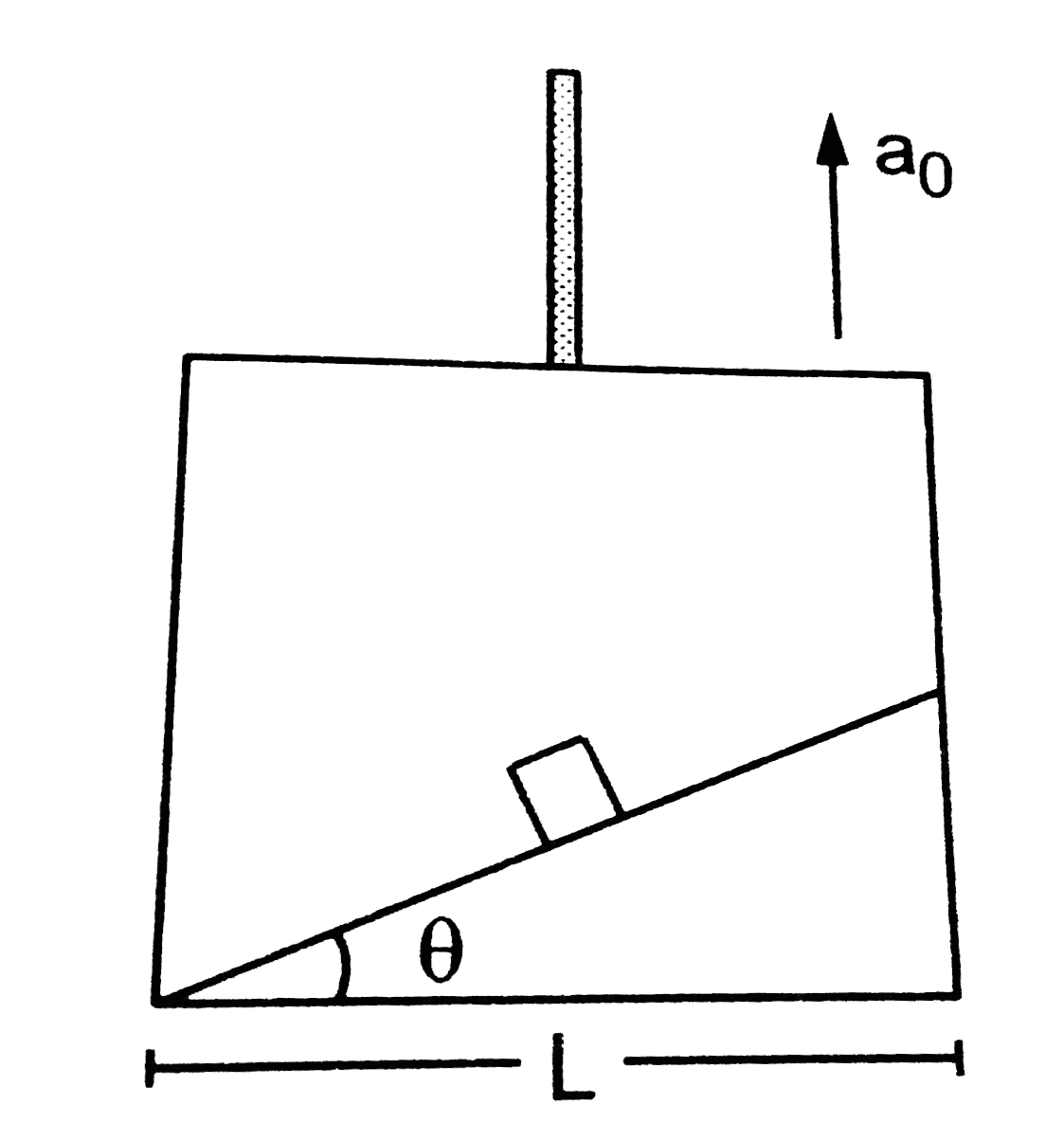
View SolutionA particle slides down a smooth inclined plane of elevation θ fixed in an elevator going up with an accelerationa0. The base of the incline has a length L.Find the time taken by the particle to reach the bottom.

View SolutionAn object is placed on the surface of a smooth inclined plane of inclination θ . It takes time t to reach the bottom of the inclined plane. If the same object is allowed to slide down rough inclined plane of same inclination θ, it takes time nt to reach the bottom where n is a number greater than 1. The coefficient of friction μ is given by -
View SolutionA body weighs 64 N on the surface of the Earth. What is the gravitational force on it (in N) due to the Earth at a height equal to one-third of the radius of the Earth?
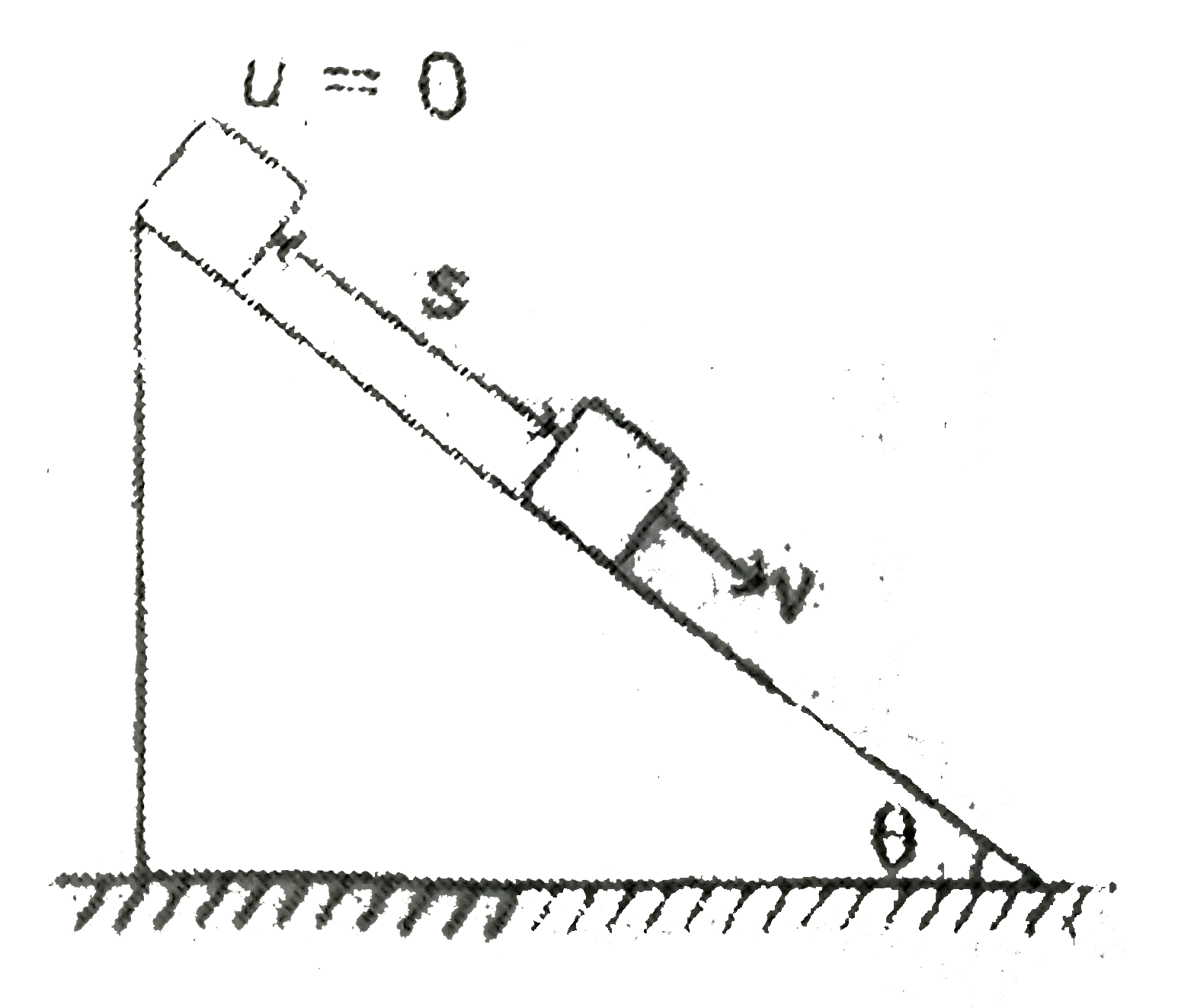
View SolutionA block is released from the top of a smooth inclined plane of inclination θ as shown in figure. Let υ be the speed of the particle after travelling a distance s down the plane. Then which of the following will remain constant ?
View SolutionA ball is projected horizontally from an inclined plane with a velocity V, as shown in the figure. It will strike the plane after a time

View SolutionA ball falls from height h over an inclined plane of inclination 30°C as shown. After the collision, the ball moves horizontally, the coefficient of restitution is
_PHY_E05_227_Q001.png)
View SolutionA ball falls from height h over an inclined plane of inclination 30∘ as shown. After the collision, the ball moves horizontally, the coefficient of restitution is
_PHY_224_Q01.png)
View SolutionA block of mass m takes time t to slide down on a smooth inclined plane of angle of inclination θ and height h. If same block slids down on a rough inclined plane of same angle of inclination and same height and takes time n times of initial value, then coefficient friction between block and inclined plane is
View Solution
