If vectors →P,→Qand→R have magnitudes 5, 12 and 13 units and →P+→Q=→R, the angle between →Qand→R is : Solution in Gujrati
cos−1(512)
cos−1(513)
cos−1(1213)
cos−1(213)
The correct Answer is:3
→P+→Q=→RandP2+Q2=R2
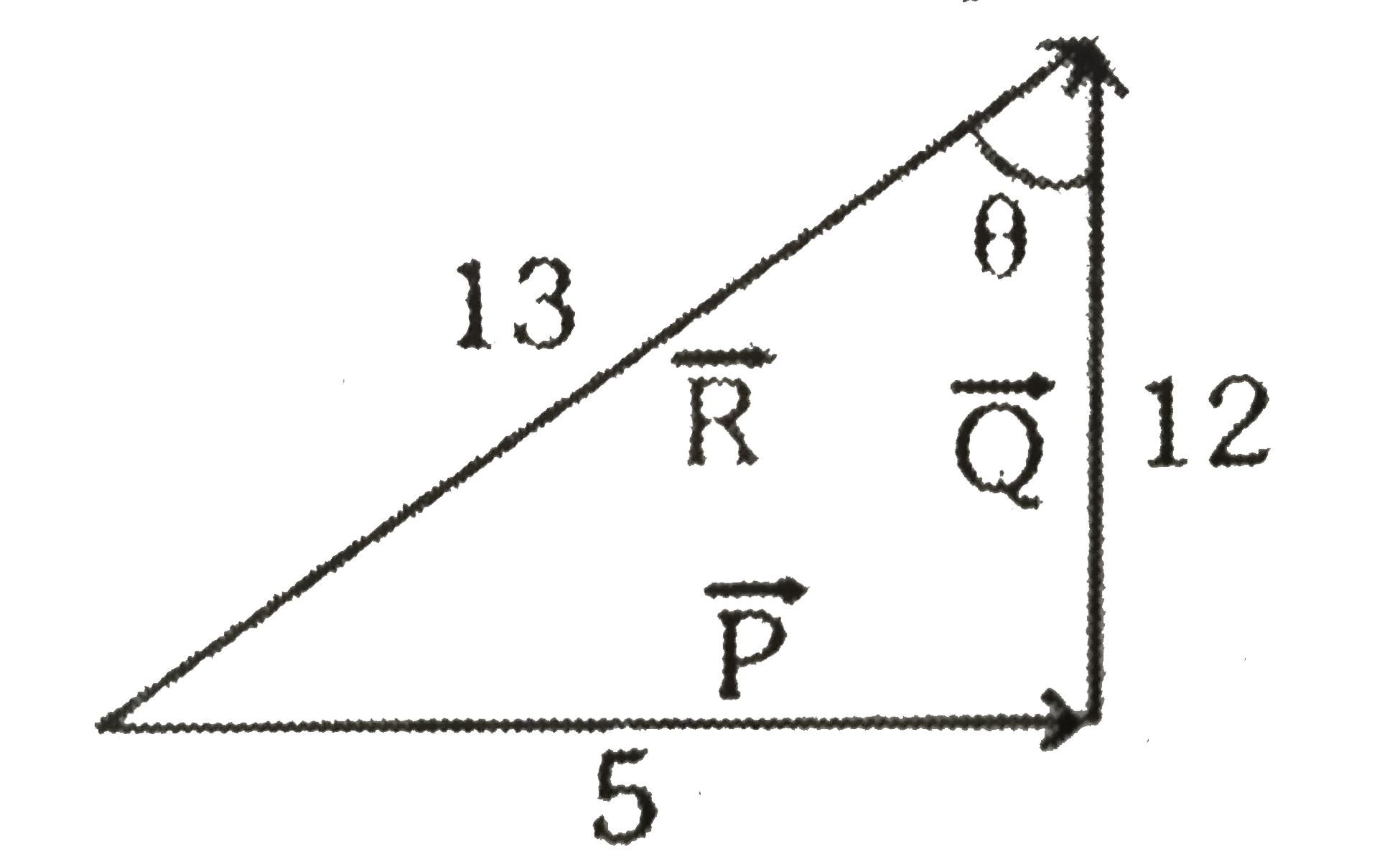
cosθ=1213⇒θ=cos−1(1213)
Topper's Solved these Questions
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLEN CHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - CROSS PRODUCT
15 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLEN CHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-II AIPMT/NEET & AIIMS (2006- 2018)
6 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLEN CHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - RESOLUTION OF VECTOR
8 Videos
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
Similar Questions
If →A=2ˆi+4ˆj and →B=6ˆi+8ˆj and A and B are the magnitudes of →A and →B, then which of the following is not true?
View SolutionThe vector →A and →B are such that ∣∣→A+→B∣∣=∣∣→A−→B∣∣. The angle between vectors →A and →B is -
View SolutionIf a unit vector is represented by 0.5ˆi+0.8ˆj+cˆk the value of c is
View SolutionTwo particles of masses m1 and m2 in projectile motion have velocities →v1 and →v2 , respectively , at time t=0. They collide at time t0. Their velocities become →v'1 and →v'2 at time 2t0 while still moving in air. The value of ∣∣∣(m1→v'1+m2→v'2)−(m1→v1+m2→v2)∣∣∣
View SolutionIf vecP+vecQ=vecR and vecP-vecQ=vecS , prove that vecR^2+vecS^2=2(vecP^2+vecQ^2)
View SolutionThree vectors →P,→Q and →R such that ∣∣→Q∣∣=A√2 and the angles between →P and →Q,→Q and →R,→R and →P are 90∘,150∘,120∘ respectivlely. Find the value of ∣∣→P∣∣=
View SolutionMagnitudes of vectors →P,→Q and →R are equal, If →P+→Q+→R=0, then angle between →Rand→Q is α while if →P+→Q=→R, the angle between →R and →P is β, then :
View SolutionIf vecP+vecQ=vecR" & "vecR is perpendicular to vecP . define angle between vecP" & "vecQ" if " vec|P|=vec|R|-
View SolutionThe sum of two forces vecP and vecQ is vecR such that |vecR|=|vecP| . The angle theta (in degrees) that the resultant of 2vecP and vecQ will make with vecQ is , _____________.
View Solutionतीन सदिश →q,→p और →r के लिए [→p,→q→r]=(→p×→q).→r=→p.(→q×→r) है फिर →p,→q→r एकटालिय होने पर [→p→q→r]=0.
माना कि →V=2ˆi+ˆj−ˆk और →W=ˆi+3ˆkयदि →U इकाई सदिश हो, तो [→U→V→W]का महत्तम मान होगा
View SolutionLet →qand→r be non - collinear vectors, If →p is a vector such that →p.(→q+→r)=4and→p×(→q×→r)=(x2−2x+9)→q then +(siny)→r
(x, y) lies on the line
View SolutionIf vecP+vecQ=vecR and |vecP|=|vecQ|=sqrt(3) and |vecR|=3 , then the angle between vecP and vecQ is
View SolutionThe resultant of vecP and vecQ is vecR . The angle between vecP and vecQ is
View SolutionThere vectors vecP, vecQ and vecR are such that vecP+vecQ+vecR=0 Vectors vecP and vecQ are equal in , magnitude . The magnitude of vector vecR is sqrt2 times the magnitude of either vecP or vecQ . Calculate the angle between these vectors .
View SolutionGiven vecP. vecQ=|vecPxxvecQ| and vecR=vecP+vecQ then |vecR| is
View SolutionIf →p,→q and →r are perpendicular to →q+→r,→r+→p and →p+→q respectively and if |→p+→q|=6,|→q+→r|=4√3 and |→r+→p|=4 then |→p+→q+→r| is
View Solution
