The centripetal force F acting on a particle moving uniformly in a circle may depend upon mass (m), velocity (v) and radius ( r) of the circle . Derive the formula for F using the method of dimensions. Solution in Gujrati
The correct Answer is:F=Kmv2r
F∝mavbrc⇒F=kmavbrc
⇒[M1L1T−2]=[M]a[L1T−1]b[L]c=[M]a[L]b+c[T]−b
by comparision a = 1, b = 2, c= -1
So F=kmv2r
Topper's Solved these Questions
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLEN CHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - BEGINNER S BOX-3
3 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLEN CHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - BEGINNER S BOX-4
4 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLEN CHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - BEGINNER S BOX-1
2 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Question
1 Videos
- SEMICONDUCTORSBOOK - ALLEN CHAPTER - SEMICONDUCTORSEXERCISE - Part-3(Exercise-4)
50 Videos
Similar Questions
Write the following in scientific notation :
(a) 3256 g
(b) 0.0010 g
(c ) 50000 g
(d) 0.3204
View SolutionRound off the following numbers as indicated:
(a) 25.653 to 3 digits (b) 4.996×105 to 3 digits (c) 0.6995 to 1 digit
(d) 3.350 to 2 digits (e) 0.03927 kg to 3 digits (f) 4.085×108s to 3 digits
View SolutionThe value of Gravitational constant G in MKS system is 6.67×10−11N−m2/kg2
What will be its value in CGS system ?
View SolutionA simple pendulum of length l and bob mass m is hanging in front of a large nonconducting sheet having surface charge density σ. If suddenly a charge +q is given to the bob & it is released from the position shown in figure. Find the maximum angle through which the string is deflected from vertical .
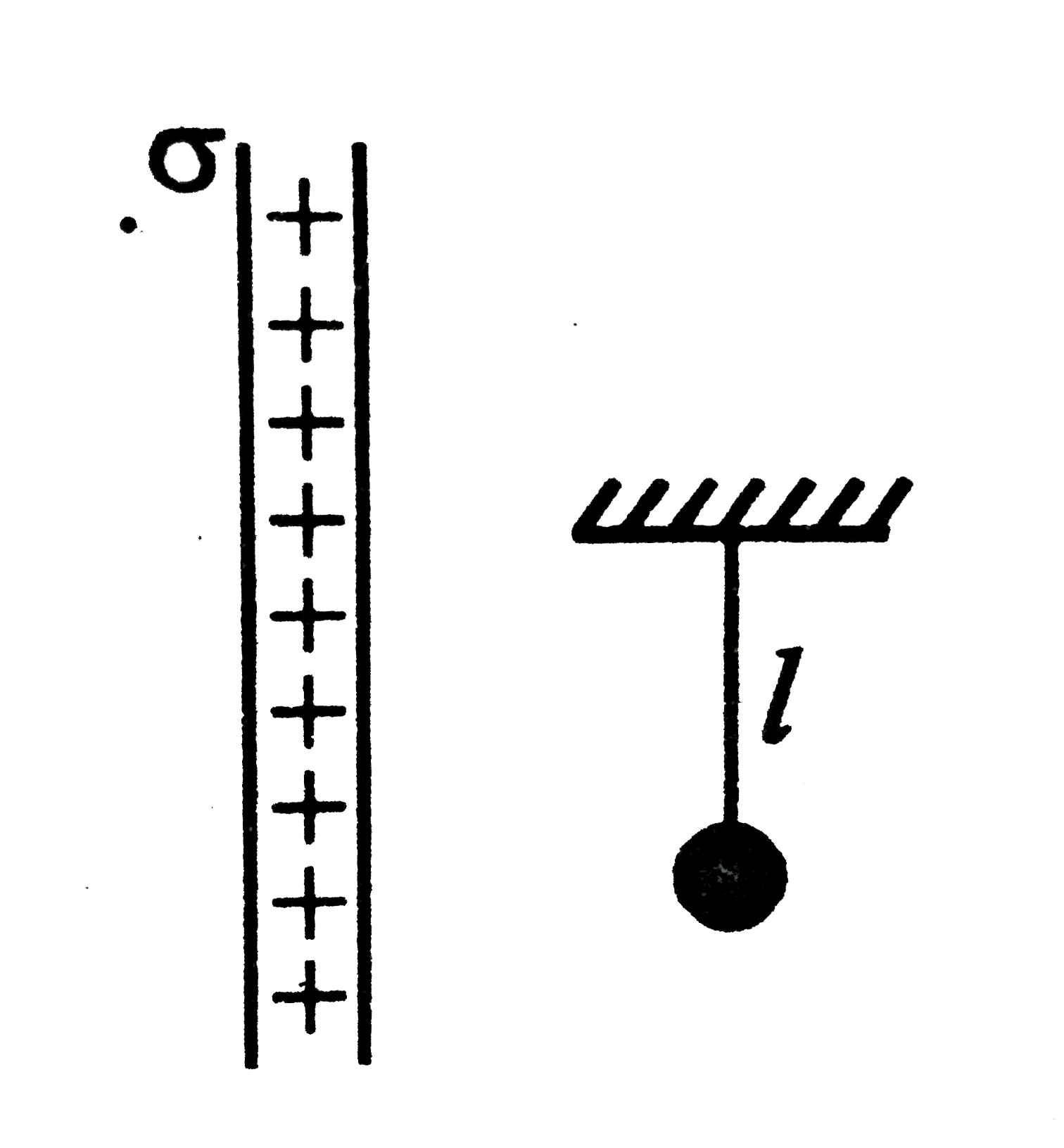 .
.
View SolutionAt absolute zero temperature Si acts as ……..
View SolutionThe contripetal force F acting on a particle moving uniformly in a circle may depend upon mass (m), velocity (v) and redio ( r) of the circle . Derive the formula for F using the method of dimensions.
View SolutionThe wavalenght (lambda) of matter waves may depends upon Planck's constant (h) mass (m) and velocity (upsilon) of the particle. Use the method of dimensions to derive the formula
View SolutionObtain an expression for the centripetal force F acting on a particle of mass m moving with velocity v in a circle of radius r . Take dimensionless constant K = 1 .
View SolutionA body of mass m is moving in a circle of radius angular velocity omega . Find the expression for centripetal force acting on it by the method of dimensions
View Solutionm द्रव्यमान का कण r त्रिज्या के वृत्त पर एकसमान कोणीय वेग ω से चक्कर लगा रहा हैं । कण पर कार्यरत अभिकेंद्र बल हैं -
View Solutionयदि अभिकेन्द्रीय बल F का मान कण के द्रव्यमान m, कण के वेग v तथा वृत्ताकार पथ की त्रिज्या r पर निर्भर करता है, तो विमीय विधि से अभिकेन्द्रीय बल का व्यंजक प्राप्त कीजिए।
View Solutionv चाल से त्रिज्या r के वृत्त में एकसमान गति करते हुए m द्रव्यमान वाले पिंड पर लगाने वाले अभिकेंद्र बल का परिमाण होता है-
View SolutionCentripetal force (F) on a body of mass (m) moving with uniform speed (v) in a circle of radius (r ) depends upon m, v and r. The formula for the centripetal force using theory of dimensons.
View SolutionObtain an expression for the centripetal force F acting on a particle of mass m moving with velocity v in a circle of radius r . Take dimensionless constant K = 1 .
View SolutionDimensionally prove the expression (mv^(2))/( r) for the centripetal force F acting on a particle of mass m moving with velocity v in a circle of radius r.
View Solution
