_E01_078_Q01.png)
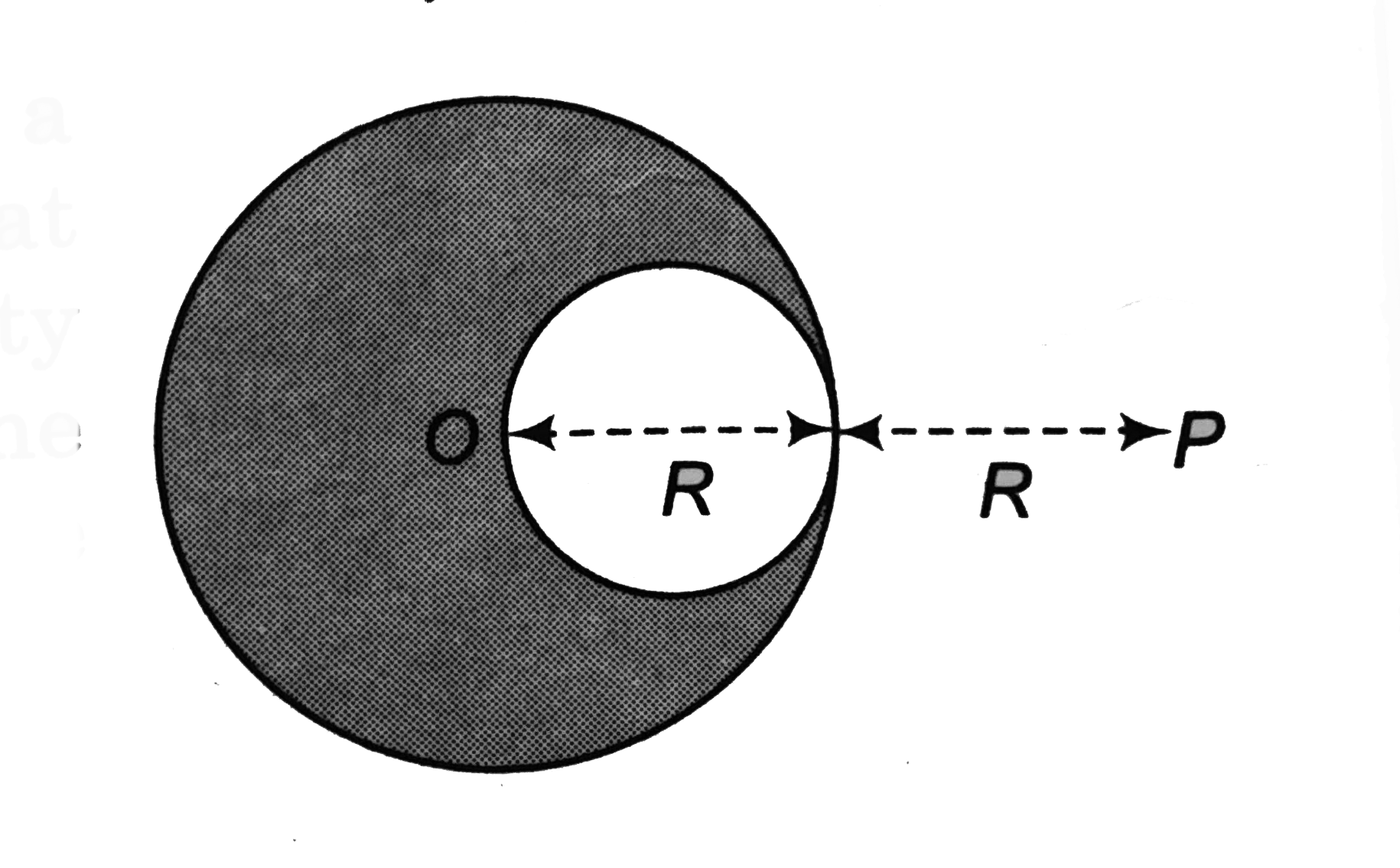
A solid sphere of uniform density and radius R applies a gravitational force of attraction equal to F1 on a particle placed at P, distance 2R from the centre of the sphere. A spherical cavity of radius R/2 is now made in te sphere as shown in figure the sphere with cavity now applies a gravitational force F2 on the same particle placed at P. find the ratio of F2/F1Solution in Gujrati
F1=GMm4R2,F2= force due to whole sphere - force due to the sphere forming the cavity
=GMm4R2−GMm18R2⇒7GMm36R2 ∴F2F1=79
Topper's Solved these Questions
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - BOX-1
3 Videos
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - BOX-2
13 Videos
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - Exercise 5 B (Previous Year Questions)
9 Videos
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective
14 Videos
- KINEMATICS-2DBOOK - ALLEN CHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
47 Videos
Similar Questions
If four different masses m1,m2,m3 and m4 are placed at the four corners of a square of side a, the resultant gravitational force on a mass m kept at the centre is
View SolutionThe magnitude of the gravitational field at distance r1 and r2 from the centre of a uniform, sphere of radius R and mass M are F1 and F2 respectively then-
View SolutionA satellite S is moving in an elliptical orbit around the earth. The mass of the satellite is very small compared to the mass of the earth.
View SolutionA prism of refractive index n1 & another prism of reactive index n2 are stuck together without a gap as shown in the figure.The angle of the prisms are as shown. n1&n2depend onλ,the wavelength of light according to n1=1.20+10.8×104λ2&n2=1.45+1.80×104λ2 where λ is in nm.

(i)Calculate the wavelength λ0for which rays incident at any angle on the interfaceBCpass through without bending at that interface.
(ii) for light of wavelength λ0,find the angle of incidencei on faceACsuch that the deviation produced by the combination of prism is minimum.
View SolutionA particle is moving in xy-plane .At certain instant the components of its velocity and acceleration are as follows ux=3m/s,uy=4m/s,ax=2m/s2anday=1m/s2. The rate of change of speed at this moment is
View SolutionA solid sphere of uniform density and radius R applies a gravitational force attraction equal to F_(1) on a particle placed at P , distance 2R from the centre O of the sphere. A spherical cavity of radius R//2 is now made in the sphere as shows in figure. The particle with cavity now applies a gravitational force F_(2) on same particle placed at P . The radio F_(2)//F_(1) will be
View SolutionThe gravitational force acting on a particle, due to a solid sphere of uniform density and radius R , at a distance of 3R from the centre of the sphere is F_1. A spherical hole of radius (R//2) is now made in the sphere as shown in diagram. The sphere with hole now exerts a force F_2 on the same particle. ratio of F_1 to F_2 is
View SolutionA solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distanace R/4 from the centre of sphere. The gravitational force on mass m is
View SolutionA uniform solid of valume mass density ρ and radius R is shown in figure.
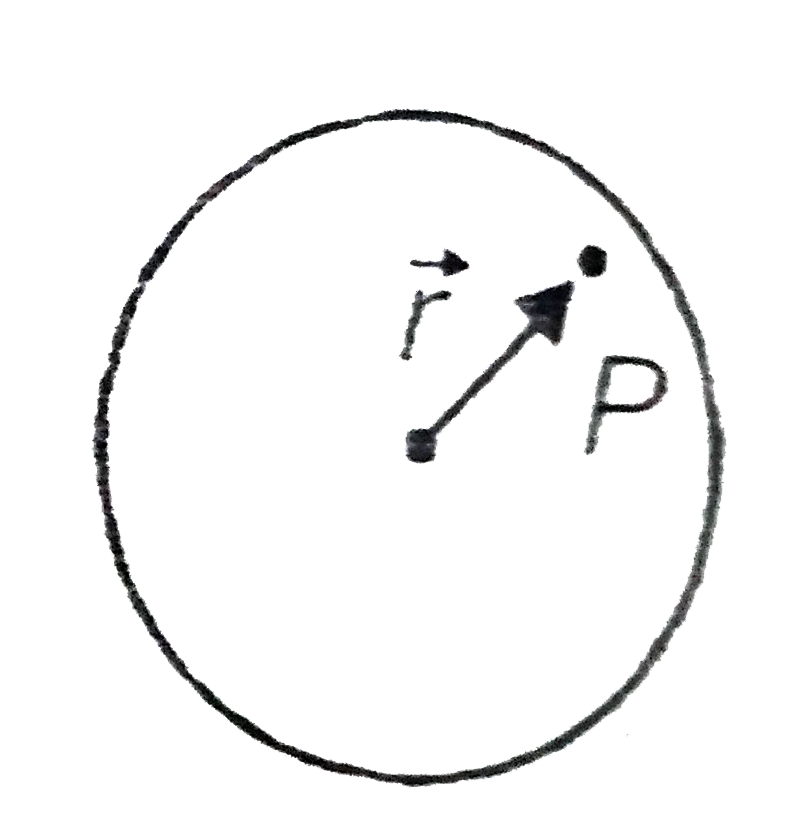
(a) Find the gravitational field at a point P inside the sphere at a distance r from the centre of the sphere. Represent the gravitational field vector →l in terms of radius vector →r of point P.
(b) Now a spherical cavity is made inside the solid sphere in such a way that the point P comes inside the cavity. The centre is at a distance a from the centre of solid sphere and point P is a distance of b from the centre of the cavity. Find the gravitational field →E at point P in vector formulationand interpret the result.
View SolutionThe gravitational force acting on a particle due to a solid sphere of uniform density and radius R, at a distance of 3R from the center of the sphere is F_1 . A spherical hole of radius (R/2) is now made in the sphere as shown in the figure . The sphere with hole now exert a force F_2 on the same particle , Ratio of F_1 and F_2 is
View SolutionA solid sphere of uniform density and radius R applies a gravitational force of attraction equal to F1 on a particle placed at P, distance 2R from the centre O of the sphere. A spherical cavity of radius R/2 is now made in the sphere as shown in figure. The particle with cavity now applies a gravitational force F2 on same particle placed at P. The radio F2/F1 will be
View Solutionत्रिज्या R व एकसमान घनत्व वाला ठोस गोला, अपने केन्द्र से 2R दूरी पर रखे एक कण पर गुरुत्वाकर्षण बल F1 लगाता है। गोले में R2 त्रिज्या की गुहा (चित्रानुसार) बनाई जाती है। अब गोला कण पर F2 बल लगाता है F1F1 मान है

View SolutionA solid sphere of uniform density and radius R applies a gravitational force of attraction equal to F_(1) on a particle placed at P , distance 2R from the centre O of the sphere. A spherical cavity of radius R//2 is now made in the sphere as shown in figure. The particle with cavity now applies a gravitational force F_(2) on same particle placed at P . The radio F_(2)//F_(1) will be
View SolutionA solid sphere of uniform density and radius R applies a gravitational force of attraction equal to F_(1) on a particle placed at P, distance 2R from the centre O of the sphere. A spherical cavity of radius R//2 is now made in the sphere as shown in given figure. The sphere with cavity now applies a gravitational force F_(2) on same particle placed at P. The ratio F_(2)//F_(1) will be
View SolutionA solid sphere of uniform density and radius R applies a gravitational force of attraction equal to F1 on a particle placed at a distance 3R from the center of the sphere. The 1 sphere with the cavity now applies a gravitational force F2, on the same particle. Then ratio F1F2 is
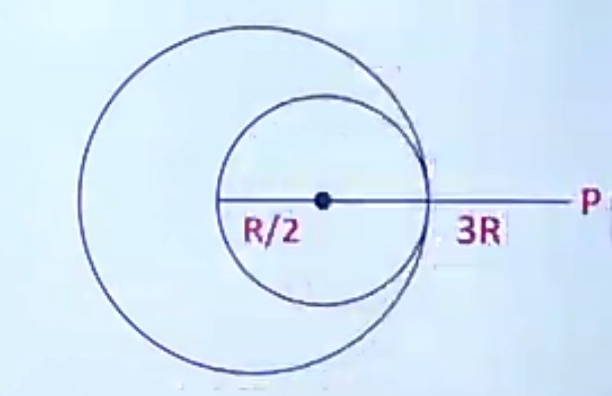
View SolutionA solid sphere of radius R gravitationally attracts a particle placed at 3R form its centre with a force F_(1) . Now a spherical cavity of radius ((R)/(2)) is made in the sphere (as shown in figure) and the force becomes F_(2) The value of F_(1) : F_(2) is:
View Solution
