a narrow tunnel is dug along the diameter of the earth, and a particle of mass m0 is placed at R2 distance from the centre. Find the escape speed of the particle from that place.
 Solution in Gujrati
Solution in Gujrati
Suppose we project the particle the particle with speed ve, so that it just reaches infinity (r→∞).
Applying energy conservation principle
Ki+Ul=Kf+Uf
12m0v2e+m0[−GMe2R3{3R2−(R2)2}]=0
⇒ve=√11GMe4R.
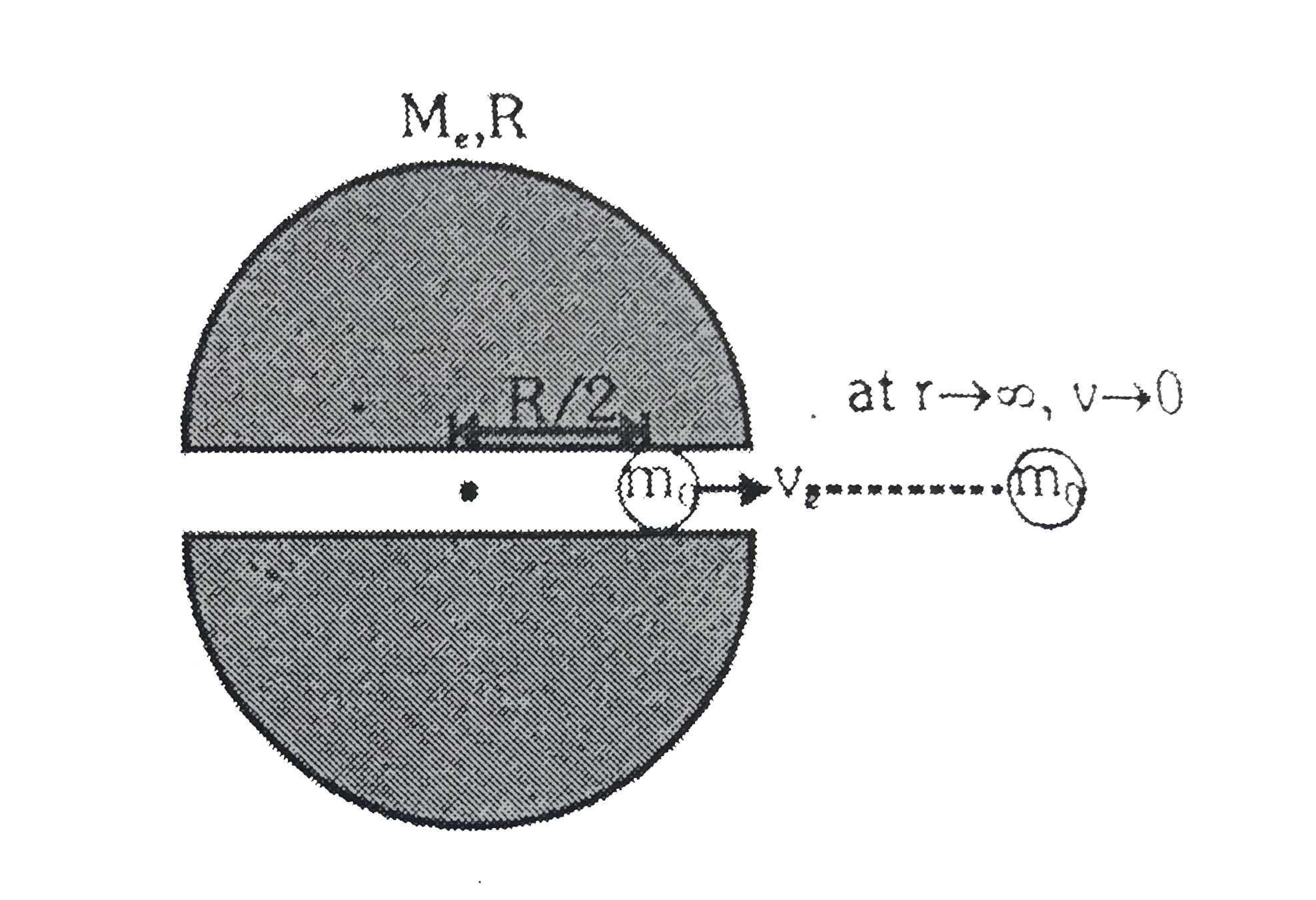
Topper's Solved these Questions
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - BOX-1
3 Videos
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - BOX-2
13 Videos
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - Exercise 5 B (Previous Year Questions)
9 Videos
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective
14 Videos
- KINEMATICS-2DBOOK - ALLEN CHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
47 Videos
Similar Questions
If four different masses m1,m2,m3 and m4 are placed at the four corners of a square of side a, the resultant gravitational force on a mass m kept at the centre is
View SolutionThe magnitude of the gravitational field at distance r1 and r2 from the centre of a uniform, sphere of radius R and mass M are F1 and F2 respectively then-
View SolutionA satellite S is moving in an elliptical orbit around the earth. The mass of the satellite is very small compared to the mass of the earth.
View SolutionA prism of refractive index n1 & another prism of reactive index n2 are stuck together without a gap as shown in the figure.The angle of the prisms are as shown. n1&n2depend onλ,the wavelength of light according to n1=1.20+10.8×104λ2&n2=1.45+1.80×104λ2 where λ is in nm.

(i)Calculate the wavelength λ0for which rays incident at any angle on the interfaceBCpass through without bending at that interface.
(ii) for light of wavelength λ0,find the angle of incidencei on faceACsuch that the deviation produced by the combination of prism is minimum.
View SolutionA particle is moving in xy-plane .At certain instant the components of its velocity and acceleration are as follows ux=3m/s,uy=4m/s,ax=2m/s2anday=1m/s2. The rate of change of speed at this moment is
View SolutionA tunnel is dug along a diameter of the earth. Find the force on a particle of mass m placed in the tunnel at a distance x from the centre.
View SolutionSuppose a tunnel is dug along a diameter of the earth. A particle is dropped from a point a distance h directly above the tunnel. The motion of the particle as seen from the earth is
View Solution(a) A tunnel is dug along a diameter of the earth. Find the force on the a particle of mass m placed in the tunnel at a distance x from the centre. (b) A tunnel is dug along a chord of the earth at a perpendicular distance R//2 from the earth's centre. the wall of the tunnel may be assumed to be frictionless. Find the force exerted by the wall on a particle of mass m when it is at a distance x from the centre of the tunnel.
View Solution_S01_013_Q01.png)
A very small groove is made in the earth, and a particle of mass m0 is placed at R2 distance from the centre. Find the escape speed of the particle fro that place.
View SolutionIf a smooth tunnel is dug across a diameter of earth and a particle is released from the surface of earth, the particle oscillate simple harmonically along it Maximum speed of the particle is
View SolutionA tunnel is dug along a diameter of the earth. Find the force in on a particle of mass m placed in the tunnel at a distance x from the centre.
View SolutionSuppose a tunnel is dug along a diameter of the earth. A particle is dropped from a point at a distance h directly above the tunnel. The motion of the particle as seen from the earth is
View SolutionA tunnel is dug along the diameter of the earth. The gravitational force on particle of mass m placed in the tunnel at a distance .x. from the centre.
View SolutionA tunnel is dug along the diameter of the earth. The gravitational force on particle of mass m placed in the tunnel at a distance .x. from the centre .
View SolutionA tunnel is dug along the diameter of the earth. The gravitational force on particle of mass m placed in the tunnel at a distance 'x' from the centre.
View SolutionA tunnel is dug along the diameter of the earth. The gravitational force on particle of mass m placed in the tunnel at a distance 'x' from the centre.
View Solution
