Position-time relationship of a particle executing simple harmonic motion is given by equation
x=2sin(50πt+2π3) where x is in meters and time t is in seconds.
What is the position of particle at t=1s ?Solution in Gujrati
√2m
√3m
1m
2 m
The correct Answer is:B
Step by step video & image solution for Position-time relationship of a particle executing simple harmonic motion is given by equation x=2sin(50pit+(2pi)/(3)) where x is in meters and time t is in seconds. What is the position of particle at t=1s ? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Differentiation)
40 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Integration)
12 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - PHYSICS
12 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLEN CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
Similar Questions
For a straight line y=43x−4. Choose correct alternate(s)
View SolutionFind the value of x1, so that ∫x10ydx=5
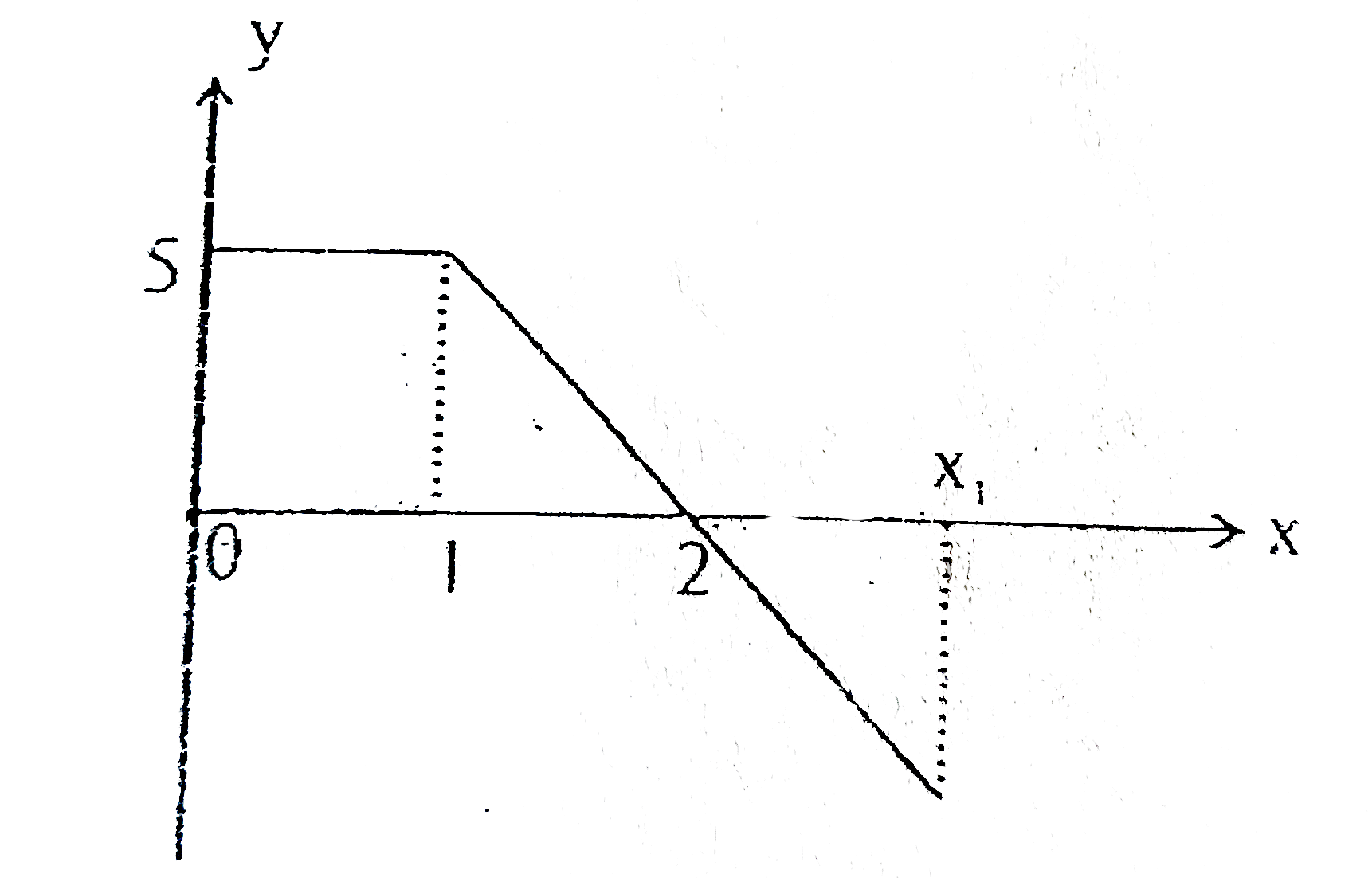
View SolutionThe graph shown the extension of is wire of length 1 m suspended from the top of a roof at one end and with a load W connected to the other end. If the cross sectional area of the wire is 1mm2, then the Young's modulus of the material of the wire.

View SolutionAssertion: The driver in a vechicle moving with a constant speed on a straight road is in a non-inertial frame of referance.
Reason: A reference frame in which Newton's laws of motion are applicable is non-inertial.
View SolutionA rod with rectangular cross section oscillates about a horizontal axis passing through one of its ends and it behaves like a seconds pendulum, its length will be
View SolutionA particle executes a simple harmonic motion of time period T. Find the time taken by the particle to go directly from its mean position to half the amplitude.
View SolutionThe position (in meters) of a particle moving on the x-axis is given by: x=2+9t +3t^(2) -t^(3) , where t is time in seconds . The distance travelled by the particle between t= 1s and t= 4s is m.
View SolutionThe position of a particle axecuting simple harmonic motion is given by
x(t)=2cos(π15t−π2), where x is in centimetre and t is in seconds. The time period of the kinetic energy of the particle in second is
View Solutionएक नियत बल के प्रभाव में कण की स्थिति एवं समय में सम्बन्ध x=(t−3)2 से दिया जाता है । जहाँ x मीटर में तथा समय t सेकंड में है तो बल द्वारा प्रथम 6 सेकंड में किये गए कार्य की गणना कीजिये ।
View Solutionएक नियत बल के प्रभाव में कण की स्थिति एवं समय में सम्बन्ध x=(t−4)2 से दिया जाता है । जहाँ पर x मीटर में तथा समय t सेकंड में है तो बल द्वारा प्रथम 8 सेकंड में किये गए कार्य की गणना कीजिये ।
View SolutionThe motion of a particle executing simple harmonic motion is given by x=0.01sin100pi(t+0.005) Where s is in metres and t in seconds. The time period in second is :
View Solutionएक विमा में गतिशील एक कण की स्थिति x समय t के साथ निम्न प्रकार परिवर्तित होती,
x=5−4t+t2
जहाँ x मीटर और t सेकण्ड में है। कण का त्वरण क्या है? (ii) वेग किस समय शून्य होता है? (iii) कण की गति का t=0 से t=3 सेकण्ड समय अन्तराल में वर्णन करो।
View SolutionExplain by plats the position of particle executing simple harmonic motion at different time.
View SolutionA particle executes a simple harmonic motion of time period T. Find the time taken by the particle to go directly from its mean position to half the amplitude.
View SolutionA particle executes simple harmonic motion with an amplitude of 10 cm and time period 6s. At t=0 it is at position x=5 cm going towards positive x-direction. Write the equation for the displacement x at time t. Find the magnitude of the acceleration of the particle at t=4s.
View SolutionA particle executes simple harmonic motion with an amplitude of 10cm and time period 6s , . At t = 0 it is at position x = 5 cm going towards positive x-direction. Write the equation for the displacement x at time t. Find the magnitude of the acceleration of the particle at t = 4 s.
View Solution
