[Gujrati] The displacement x of particle moving in one dimension, unde

Find the value of $x_{1}$ , so that $\int_{0}^{x_{1}} y d x = 5$
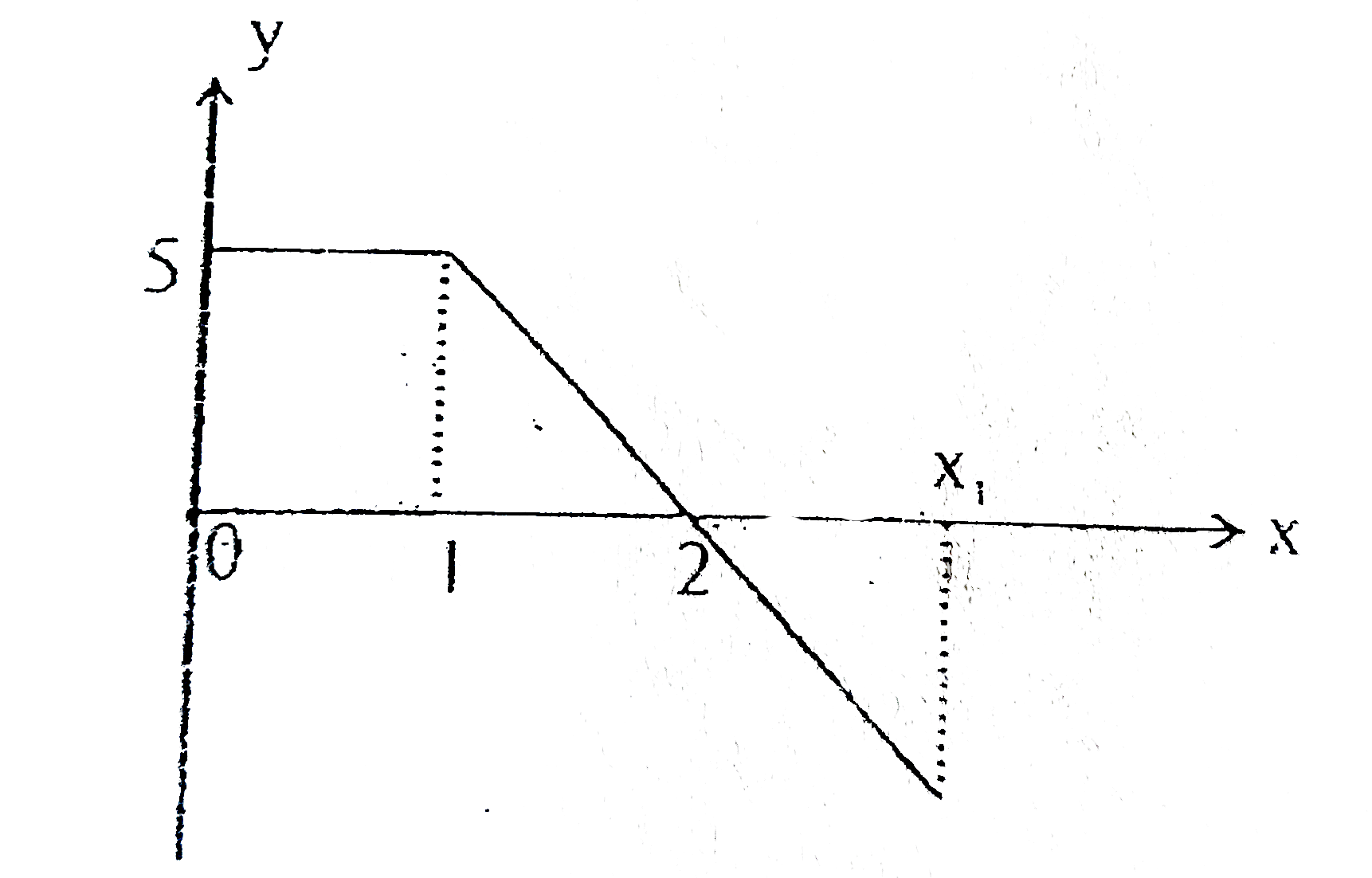
ocr_image

Which of the following equation is best representation of following graph's?
ocr_image

Convert the angle from degree to radian :
$\begin{matrix} (a) 30^{\circ} & (b) 45^{\circ} (c) 60^{\circ} & (d) 90^{\circ} (e) 120^{\circ} & (f) 135^{\circ} (g) 210^{\circ} & (h) 270^{\circ} (i) 315^{\circ} \end{matrix}$

View Solution

Assertion: The driver in a vechicle moving with a constant speed on a straight road is in a non-inertial frame of referance.
Reason: A reference frame in which Newton's laws of motion are applicable is non-inertial.

View Solution

A rod with rectangular cross section oscillates about a horizontal axis passing through one of its ends and it behaves like a seconds pendulum, its length will be

View Solution

The displacement x of particle moving in one dimension, under the action of a constant force is related to the time t by the equation t = sqrt(x) +3 where x is in meters and t in seconds . Find (i) The displacement of the particle when its velocity is zero , and (ii) The work done by the force in the first 6 seconds .

View Solution

The displacement x of a particle moving in one dimension under the action of a constant force is related to time t by the equation t=sqrt(x)+3 , where x is in meter and t is in second. Find the displacement of the particle when its velocity is zero.

View Solution

The displacement x of a particle moving in one dismension under the action of a constant force is frlated to time t by the equation tsqrtx+3 , where x is in merers and t is in seconds, Find the displacemect of the particle when its velocity is zero.

View Solution

The displacement x in meter of a particle of mass $m k g$ moving in one dimenstion under the action of a force is related to the time t in second by the equation $x = {(t - 3)}^{2}$ . The work done by the force (in joules) in first six seconds is

View Solution

The displacement 'x' (in meter) of a particle of mass 'm' (in kg) moving in one dimension under the action of a force is released to time 't' (in sec) by t = sqrt(x) + 3 . The displacement of the particle when its velocity is zero will be.

View Solution

The displacement x of a particle of mass 1.0 kg moving the one dimension under the action of a force is related to time t by the equation t=sqrt(x)+5 where x is in meter and t is in second. The magnitude of the momentum of the particle

View Solution

The displacement x in meters of a particle of mass m kg moving in one dimension under the action of a force is related to the time t in seconds by the equation $t = \sqrt{x} + 3$ , , the work done by the force (in J) in first six seconds is :-

View Solution

The displacement x of a particle moving in one dimension under the action of a constant force is related to time t by the equation t = sqrt(x+3) where x is in meters and t is in seconds. Finds the displacement (in metres ) of the particle when its velocity is zero.

View Solution

The displacement of a particle moving in one dimension under the action of a constant force is related to timer by the equation t= sqrt(x + 3) , where x is in metres and in second. What is the displacement of particle when its velocity is zero?

View Solution

The displacement x of a particle moving in one dimension under the action of a constant force is related to the time t by the equation $t = \sqrt{x} + 3$ , where x is in metre and t is in second. The work done by the force in the first 6 second is

View Solution

The correct Answer is:A

Topper's Solved these Questions

Similar Questions

ALLEN -RACE-Basic Maths (Differentiation)