A particle moves along X-axis in such a way that its coordinate X varies with time t according to the equation x=(2−5t+6t2)m. The initial velocity of the particle is Solution in Gujrati
−5 m/s
−3 m/s
6 m/s
2 m/s
The correct Answer is:A
Step by step video & image solution for A particle moves along X-axis in such a way that its coordinate X varies with time t according to the equation x = (2-5t +6t^(2))m. The initial velocity of the particle is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Integration)
12 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Graphs))
28 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Trigonometry)
22 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLEN CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
Similar Questions
Find the value of x1, so that ∫x10ydx=5
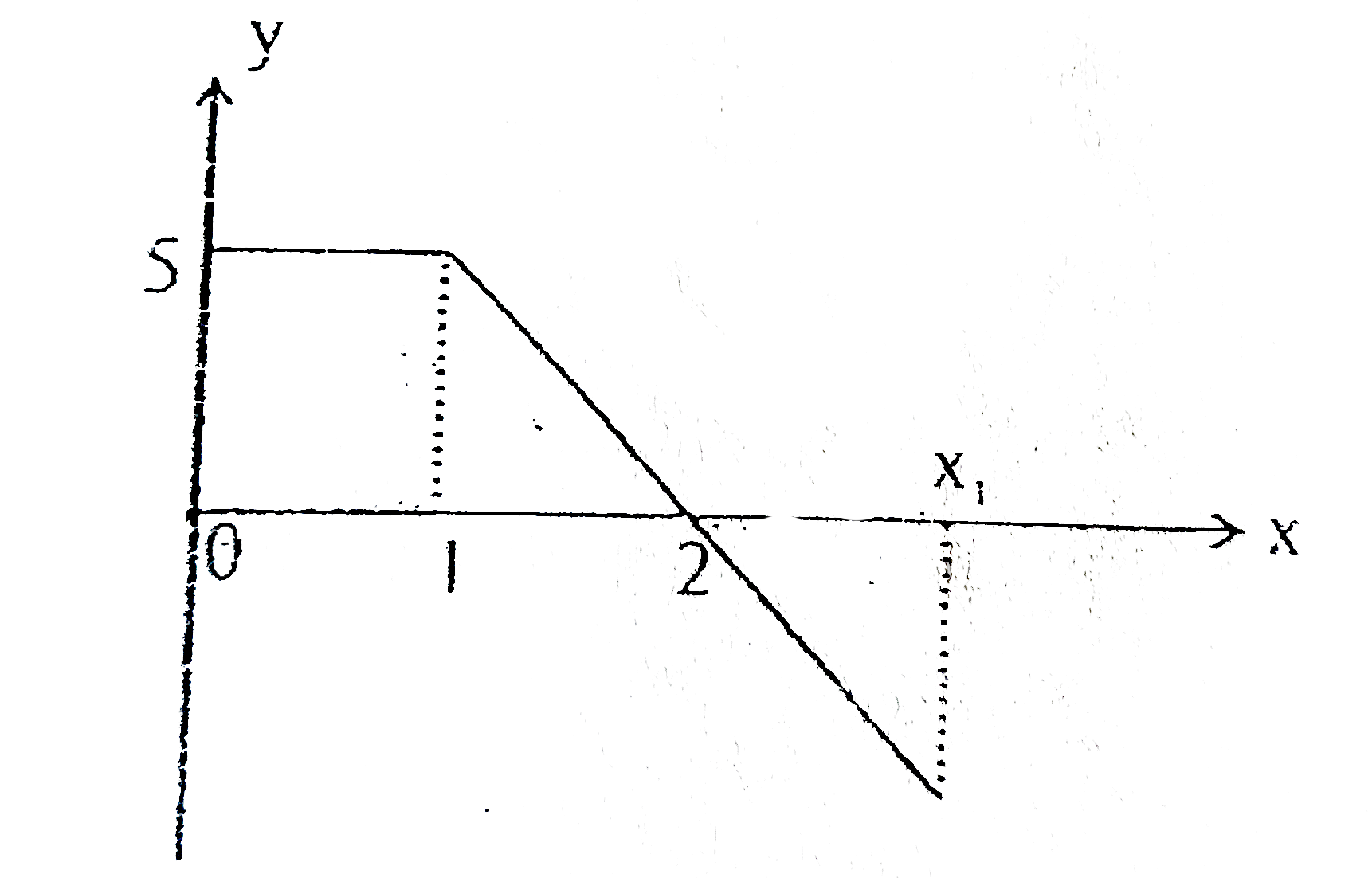
View SolutionWhich of the following equation is best representation of following graph's?
View SolutionConvert the angle from degree to radian :
(a) 30∘(b) 45∘(c) 60∘(d) 90∘(e) 120∘(f) 135∘(g) 210∘(h) 270∘(i) 315∘
View SolutionAssertion: The driver in a vechicle moving with a constant speed on a straight road is in a non-inertial frame of referance.
Reason: A reference frame in which Newton's laws of motion are applicable is non-inertial.
View SolutionA rod with rectangular cross section oscillates about a horizontal axis passing through one of its ends and it behaves like a seconds pendulum, its length will be
View SolutionVelocity (in m/s) of a particle moving along x-axis varies with time as, v= (10+ 5t -t^2) At time t=0, x=0. Find (a) acceleration of particle at t = 2 s and (b) x-coordinate of particle at t=3s
View SolutionA particle moves along x axis in such a way that its coordinate x varies with time t according to the equation x = A_0 - A_1 t + A_2 t^2 . The initial velocity of the particle is.
View SolutionA particle moves in an XY-plane in such a way that its x and y-coordinates vary with time according to x(t)=t^(3)-32t, y(t)=5t^(2)+12 Find the acceleration of the particle, if t = 3 s.
View SolutionA particle moves along x-axis in such a way that its x-coordinate varies with time t according to the equation x=(8−4t+6t2) metre.
The velocity of the particle will vary with time according to the graph :-
View SolutionA particle moves along the x-axis such that its co-ordinate (x) varies with time (t), according to the expression x=2−5t+6t2, where x is in metres and t is in seconds. The initial velocity of the particle is :–
View Solutionएक कण X - अक्ष के अनुदिश इस प्रकार गति करता है कि उसका x - निर्देशांक समय t के साथ निम्न समीकरण के अनुसार बदलता है −x=(2−5t+6t2),
जहाँ x, मीटर में तथा t सेकंड में है। कण का प्रारंभिक वेग ज्ञात कीजिये ।
View Solutionएक कण X - अक्ष के अनुदिश इस प्रकार गति करता है कि उसका x - निर्देशांक समय t के साथ निम्न समीकरण के अनुसार बदलता है −x=(2−5t+6t2),
जहाँ x, मीटर में तथा t सेकंड में है। कण का प्रारंभिक वेग ज्ञात कीजिये ।
View SolutionA particle moves along the x-axis in such a way that its x-co-ordinate varies with time as x = 2 – 5t + 6t^(2) . The initial velocity and acceleration of particle will respectively be-
View SolutionA particle moves along x - axis in such a way that its x - co - ordinate varies with time according to the equation x=4-2t+t^(2) . The speed of the particle will vary with time as
View SolutionA particle moves along the x-axis in such a way that its coordinates x varies with time 't' according to the equation x=2-5t+6t^(2) . What is the initial velocity of the particle?
View SolutionA particle moves along x-axis in such a way that its r-coordinate varies with time't according to the equation x= (8−4t+6t2) metre. The velocity of the particle will vary with time according to the graph
View Solution
