The slope of graph in figure at point A, B and C is mA,mB and mC respectively, then :
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R04_E01_017_Q01.png" width="80%"gtSolution in Gujrati
mA>mB>m(C)
mA<mB<mC
mA=mB=mC
mA=mC<mB
The correct Answer is:B
Step by step video & image solution for The slope of graph in figure at point A, B and C is m_(A), m_(B)" and "m_(C) respectively, then : ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R04_E01_017_Q01.png" width="80%"gt by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Co-ordinate & Algebra)
40 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (VECTORS)
62 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Integration)
12 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLEN CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
Similar Questions
Find the value of :-
(i)√4
(ii)√9
(iii)√16
(iv)sqrt(36)
View SolutionState whether the following relations are true or false
(1)−−→AB=−−→BA
(2)−−→AB=−−−→BA
(3)∣∣∣−−→AB∣∣∣=∣∣∣−−→BA∣∣∣
(4)∣∣∣−−→AB∣∣∣=∣∣∣−−−→AB∣∣∣
(5)ˆj=ˆk
(6)∣∣ˆj∣∣=∣∣ˆk∣∣
View SolutionFind the value of x1, so that ∫x10ydx=5
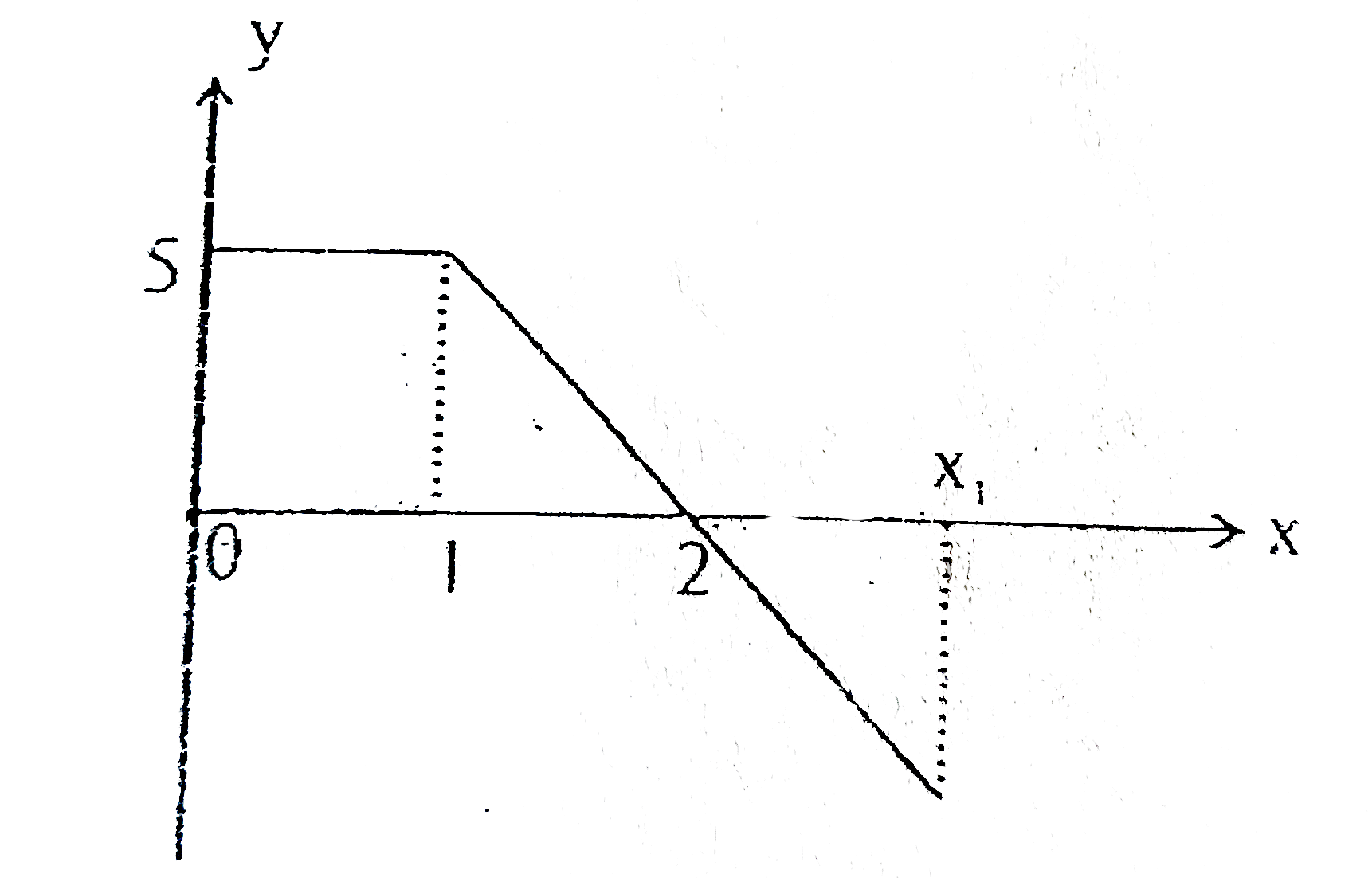
View SolutionAssertion: The driver in a vechicle moving with a constant speed on a straight road is in a non-inertial frame of referance.
Reason: A reference frame in which Newton's laws of motion are applicable is non-inertial.
View SolutionA rod with rectangular cross section oscillates about a horizontal axis passing through one of its ends and it behaves like a seconds pendulum, its length will be
View SolutionThe slope of graph as shown in figure at points 1,2 and 3 is m1,m2 and m3 respectively then
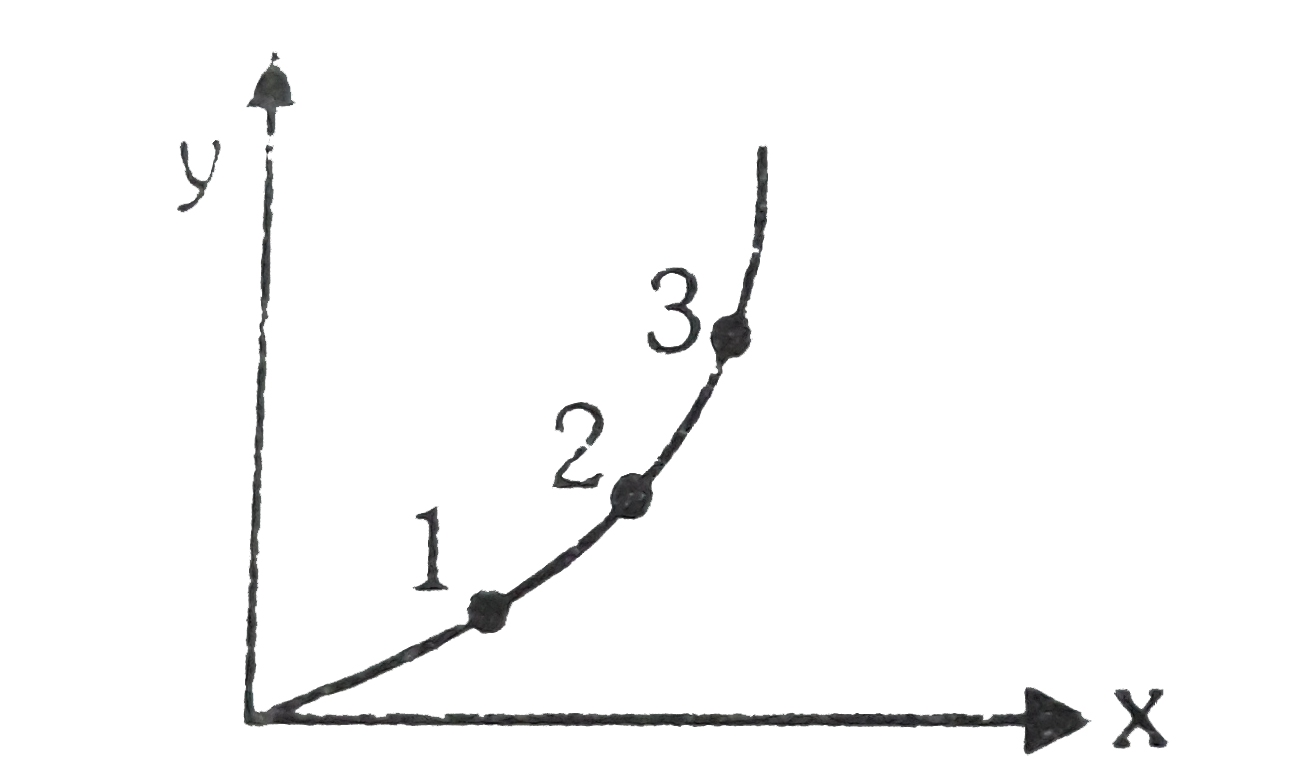
View SolutionIn ΔABC, if ma,mb,mc denote the lengths of the medians drawn to the sides a, b, c respectively and Δ is the area of the ΔABC with a=10,c=6 and mb=7then
View SolutionThree blocks are placed as shown in figure. Mass of A, B and C are m_(1), m_(2),"and "m_(3) respectively. The force exerted by block 'C' on 'B' is :-
View SolutionLet ABC be a triangle inscribed in a circle and let la=maMa,lb=mbMb,lc=mcMc where ma,mb,mc are the lengths of the angle bisectors of angles A, B and C respectively , internal to the triangle and Ma,MbandMc are the lengths of these internal angle bisectors extended until they meet the circumcircle.
Q. la equals :
View SolutionLet ABC be a triangle inscribed in a circle and let la=maMa,lb=mbMb,lc=mcMc where ma,mb,mc are the lengths of the angle bisectors of angles A, B and C respectively , internal to the triangle and Ma,MbandMc are the lengths of these internal angle bisectors extended until they meet the circumcircle.
Q. The maximum value of the product (lalblc)×cos2(B−C2)×cos2(C−A)2)×cos2(A−B2) is equal to :
View SolutionLet ABC be a triangle inscribed in a circle and let la=maMa,lb=mbMb,lc=mcMc where ma,mb,mc are the lengths of the angle bisectors of angles A, B and C respectively , internal to the triangle and Ma,MbandMc are the lengths of these internal angle bisectors extended until they meet the circumcircle.
Q. The minimum value of the expression lasin2A+lbsin2B+lcsin2C is :
View SolutionIf the length of medians AA1,BB1 and CC1 of △ABC are ma,mb and mc respectively, then:
View SolutionLet ABC be a triangle inscribed in a circle and let la=maMa,lb=mbMb,lc=mcMc where ma,mb,mc are the lengths of the angle bisectors of angles A, B and C respectively , internal to the triangle and Ma,MbandMc are the lengths of these internal angle bisectors extended until they meet the circumcircle.
Q. la equals :
View SolutionLet ABC be a triangle inscribed in a circle and let la=maMa,lb=mbMb,lc=mcMc where ma,mb,mc are the lengths of the angle bisectors of angles A, B and C respectively , internal to the triangle and Ma,MbandMc are the lengths of these internal angle bisectors extended until they meet the circumcircle.
Q. The maximum value of the product (lalblc)×cos2(B−C2)×cos2(C−A)2)×cos2(A−B2) is equal to :
View SolutionLet ABC be a triangle inscribed in a circle and let la=maMa,lb=mbMb,lc=mcMc where ma,mb,mc are the lengths of the angle bisectors of angles A, B and C respectively , internal to the triangle and Ma,MbandMc are the lengths of these internal angle bisectors extended until they meet the circumcircle.
Q. The minimum value of the expression lasin2A+lbsin2B+lcsin2C is :
View SolutionIn triangle ABC m1,m2,m3 are the lenghts of the medians through A,B and C respectively . If C=π2, then m21+m22m23=
View Solution
