A particle projected from origin moves in x-y plane with a velocity →v=3ˆi+6xˆj, where ˆi and ˆj are the unit vectors along x and y axis. Find the equation of path followed by the particle :-Solution in Gujrati
y=x2
y=1x2
y=2x2
y=1x
The correct Answer is:A
Step by step video & image solution for A particle projected from origin moves in x-y plane with a velocity vecv=3hati+6xhatj, where hati" and "hatj are the unit vectors along x and y axis. Find the equation of path followed by the particle :- by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (NEWTONS LAWS OF MOTION)
49 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (FRICTION)
13 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Units, Dimensions & Measurements)
37 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLEN CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
Similar Questions
There are two bodies A & B of same mass body A is at rest while body B is under going uniform motion, which is correct statements ?
View SolutionA block of mass 1 kg is plased on a surgace for which μs=0.2&μk=0.15, an external force F is applied on the block as shown in the figure, using g=10m/sec2, find:
(a) The force of friction on block
(b) Its acceleration
(i) When F=1 N
(ii) When F=2 N
(iii) When F=2.5 N

View SolutionWhich one of the following is not a fundamental quantity ?
View SolutionAssertion: The driver in a vechicle moving with a constant speed on a straight road is in a non-inertial frame of referance.
Reason: A reference frame in which Newton's laws of motion are applicable is non-inertial.
View SolutionA rod with rectangular cross section oscillates about a horizontal axis passing through one of its ends and it behaves like a seconds pendulum, its length will be
View SolutionA particle is projected in xy plane with y-axis along vertical, the point of projection is origin. The equation of the path is y=√3x−g2x2.where y and x are in m.Then the speed of projection in ms−1 is
View SolutionA particle whose velocity is given as vecv=hati+6thatjm//s is moving in x-y plane. At t-0, particle is at origin. Find the radius of curvature of path at point ((sqrt(2))/(3)m,(2)/(3)m)
View SolutionTwo unit vectors ˆi and ˆj are directed along x-axis and y-axis respectively. What is the magnitude and direction of the vectors ˆi+ˆjandˆi−ˆj?
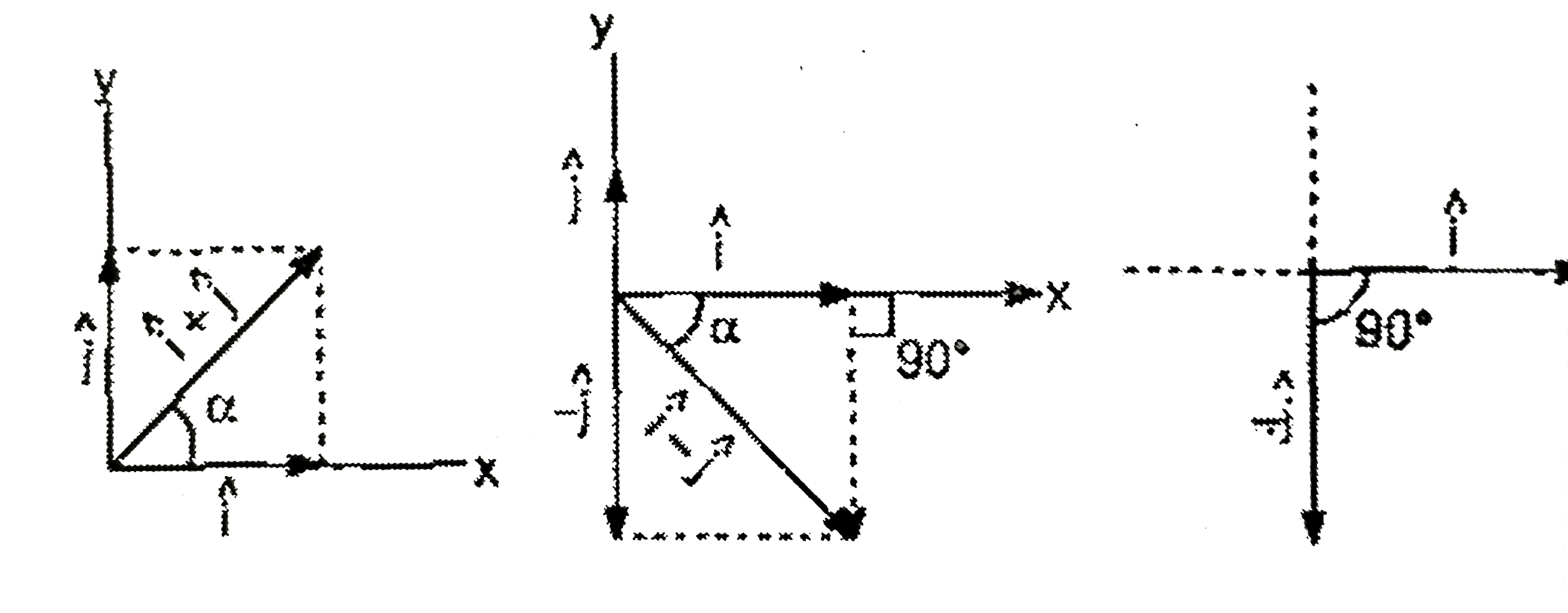
View SolutionThe instantaneous velocity of a particle moving in xy-plane is →V=(ay)ˆi+(V0)ˆj where y is the instantaneous y co-ordinat of the particle and V0 is the particle starts from origin then its trajectory is
View SolutionThe velocity of a particle is vecv=3hati+2hatj+3hatk .Find the vector component of the velocity along the line hati-hatj+hatk and its magnitude.
View SolutionIf hati and hatj are unit vectors along X-and Y-axis respective, then what is the magnitude and direction of hati +hatj and hati - hatj ?
View SolutionA particle projected from origin moves in x-y plane with a velocity vecv=3hati+6xhatj , where hati" and "hatj are the unit vectors along x and y axis. Find the equation of path followed by the particle :-
View Solutionm द्रव्यमान का एक छोटा कण Xअक्ष से θ कोण पर प्रारम्भिक वेग v0 से x-y तल में चित्रानुसार प्रक्षेपित किया गया है। समय t<v0sinθg पर कण का कोणीय संवेग है:
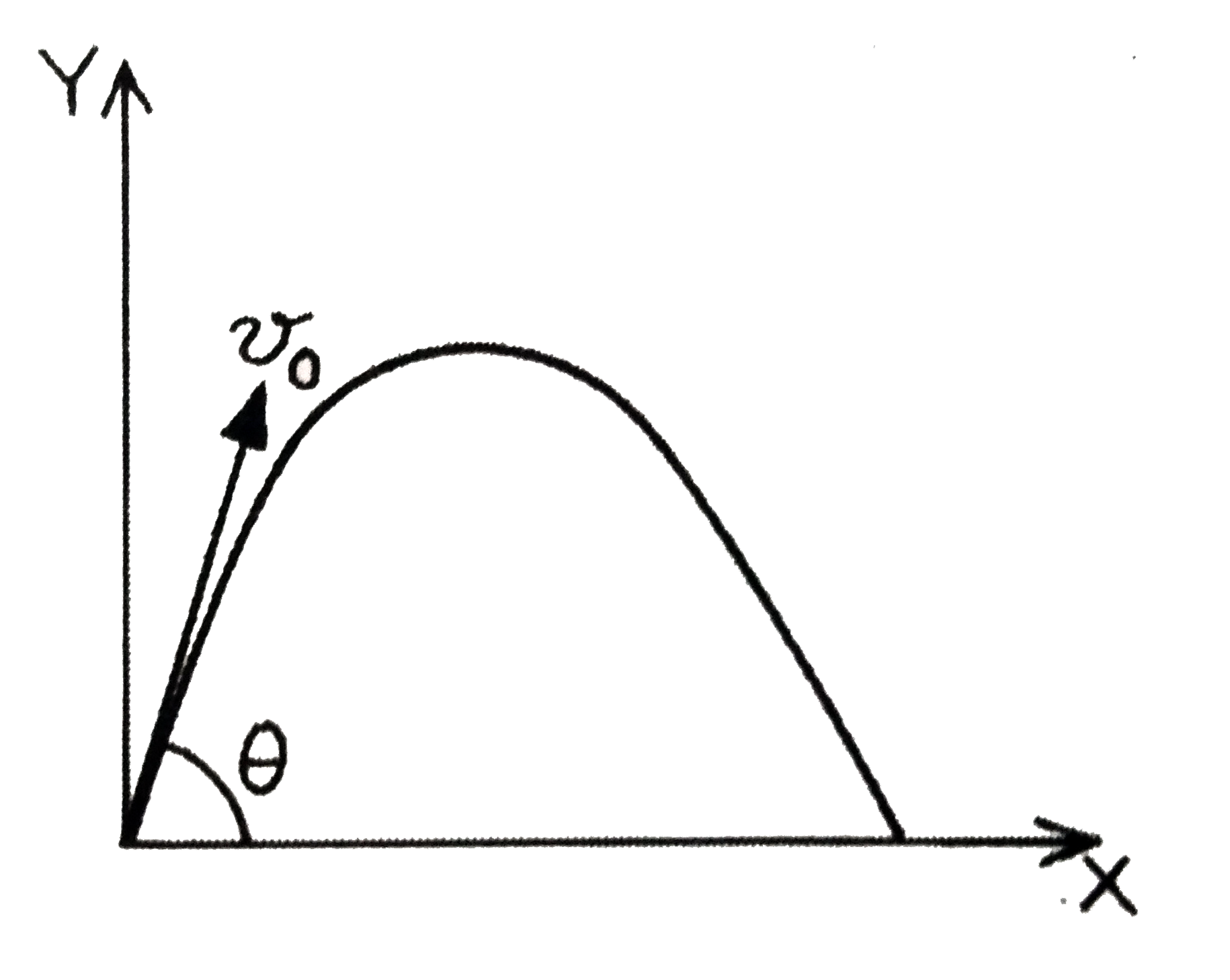
जहां ˆi,ˆj,ˆk,x−,y− तथा z- अक्ष के अनुदिश एकांक सदिश है।
View SolutionX-Y-तल में गतिमान एक कण पर एक बल →F=−k(yˆi+xˆj) (जहाँ k एक धन नियतांक है ) लगता है | मूल-बिंदु से प्रारम्भ करके, कण को धनात्मक X-अक्ष के अनुदिश बिंदु (a,0 ) तक ले जाया जाता है तथा फिर Y-अक्ष के समांतर बिंदु (a, a) तक | कण पर बल →F द्वारा किया गया कुल कार्य है :
View Solutionˆiandˆj are unit vectors along x and y axis. What is the magnitude and direction of the vector ˆi+ˆj ?
View SolutionA particle is projected from the origin in X-Y plane. Acceleration of particle in Y direction is a. If equation of path of the particle is y=ax−bx2, then find initial velocity of the particle.
View Solution
