A particle moving on x - axis has potential energy U=2−20x+5x2 joule along x - axis. The particle is relesed at x=−3. The maximum value of x will be (x is in metre)Solution in Gujrati
5 m
3 m
7 m
8 m
The correct Answer is:C
Step by step video & image solution for A particle moving on x - axis has potential energy U = 2 - 20x + 5x^(2) joule along x - axis. The particle is relesed at x = -3. The maximum value of x will be (x is in metre) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Oscillations) (Simple pendulum and types of SHM)
17 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Fundamental)
24 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Dscillations) (Kinematics of SHM)
20 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLEN CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
Similar Questions
Two pendulums of length 1.21 m and 1.0 m starts vibrationg. At some instant, the two are in the mean position in same phase. After how many vibrations of the longer pendulum, the two will be in phase ?
View SolutionLet speed of sound waves in hydrogen gas at room temperature is v0. What will be the speed of sound waves in a room which contains an equimolar mixture of hydrogen and 'He' at same temperature :-
View SolutionTwo particles executing SHM of same frequency meet at x=+√3A2, while moving in opposite directions. Phase difference between the particles is :-
View SolutionAssertion: The driver in a vechicle moving with a constant speed on a straight road is in a non-inertial frame of referance.
Reason: A reference frame in which Newton's laws of motion are applicable is non-inertial.
View SolutionA rod with rectangular cross section oscillates about a horizontal axis passing through one of its ends and it behaves like a seconds pendulum, its length will be
View SolutionPotential energy of a particle moving along x-axis is by
U=(x33−4x+6).
here, U is in joule and x in metre. Find position of stable and unstable equilibrium.
View SolutionA particle moving on x - axis has potential energy U = 2 - 20x + 5x^(2) joule along x - axis. The particle is relesed at x = -3 . The maximum value of x will be ( x is in metre)
View SolutionA single conservative force F(x) acts on a 1.0−kg particle that moves along the x-axis. The potential energy U(x) is given by U(x)=20+(x−2)2 where x is in meters. At x=5.0m, the particle has a kinetic energy of 20J.
The maximum and minimum values of x, respectively, are
View SolutionA particle free to move along the X- axis has potential energy given by U(X)=k[1-exp(-X^(2))] of appropriate dimensions. Then-
View SolutionA single conservative f(x) acts on a m=1kg particle moving along the x-axis. The potential energy U(x) is given by :
U(x)=20+(x−2)2
where x is in metres. At x=5m, a particle has kintetic energy of 20 J
The maximum value of potential energy is:
View SolutionA single conservative force F(x) acts on a particle that moves along the x - axis. The graph of the potential energy with x is given. At x=5m, the particle has a kinetic energy of 50 J and its potential energy is related to position 'x' as U=15+(x−3)2 Joule where x is in meter. Then:
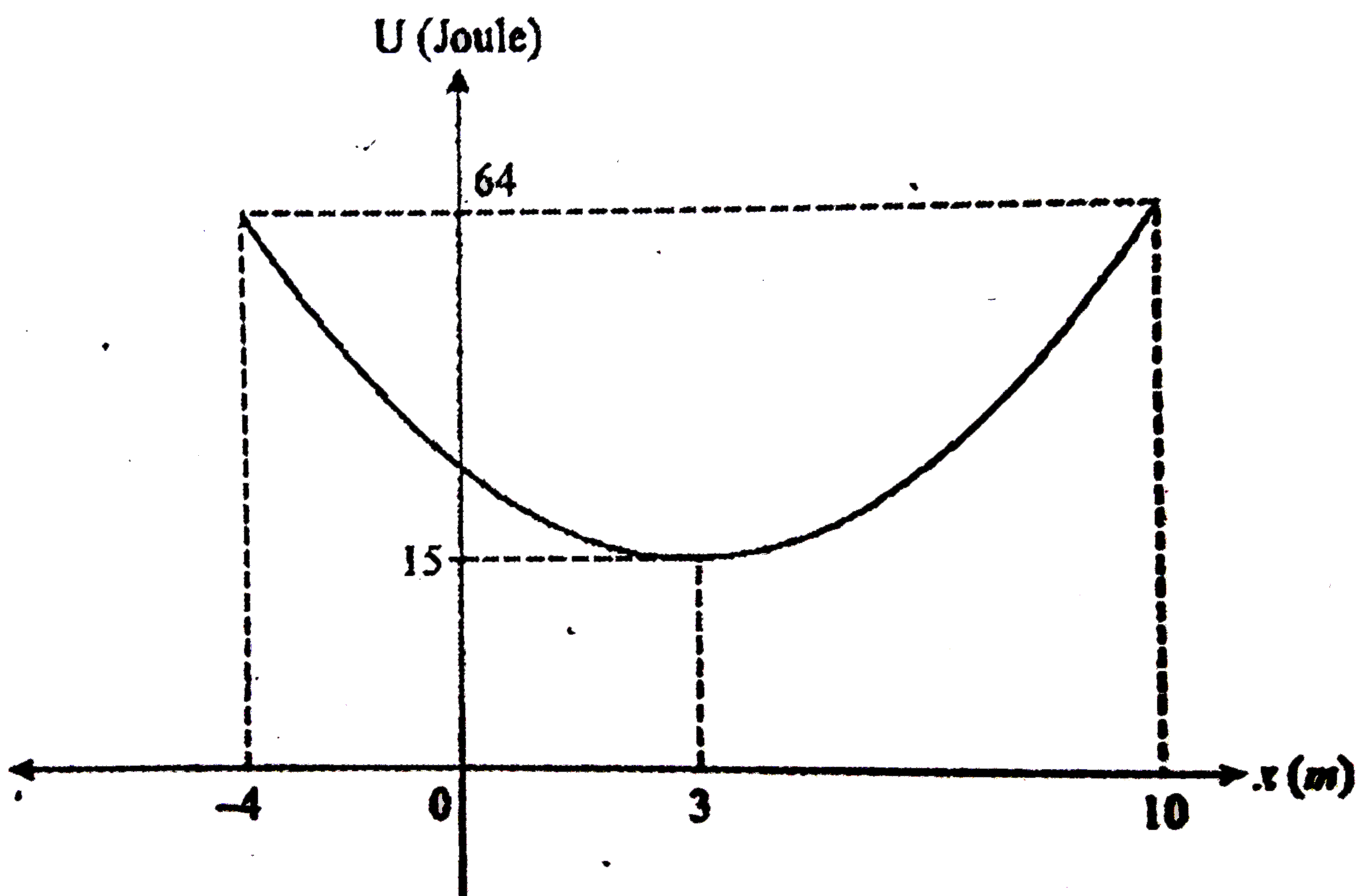
View SolutionX - अक्ष पर स्वतन्त्र रूप से दोलन कर रहे 1 किग्रा द्रव्यमान के कण की स्थितिज ऊर्जा U=x42−x22 जूल है | यदि कण की सम्पूर्ण यांत्रिक ऊर्जा 6 जूल है तो उसकी अधिकतम चाल होगी :
View SolutionThe potential energy U(x) of a particle moving along x - axis is given by U(x)=ax-bx^(2) . Find the equilibrium position of particle.
View SolutionThe potential energy of 1kg particle free to move along x-axis is given by U(x)=[x^4/4-x^2/2]J. The total mechanical energy of the particle is 2J. The maximum speed of the particle is
View Solutionएक कण, जो कि x-अक्ष के अनुदिश गति कर रहा है, का समीकरण है x=u(t−2)+a(t−2)2 एक कण, जो कि X-अक्ष के अनुदिश गति कर रहा है, का समीकरण है x=u(t−2)+a(t−2)2
View SolutionThe potential energy of a particle oscillating on x-axis is given as U = 20 + (x-2)^(2) where .U. is in joules and .x. is in metres. Its mean position is
View Solution
