Two identical spring of constant K are connected in series and parallel as shown in figure. A mass is suspended from them. The ratio of their frequencies of vertical oscillations will be 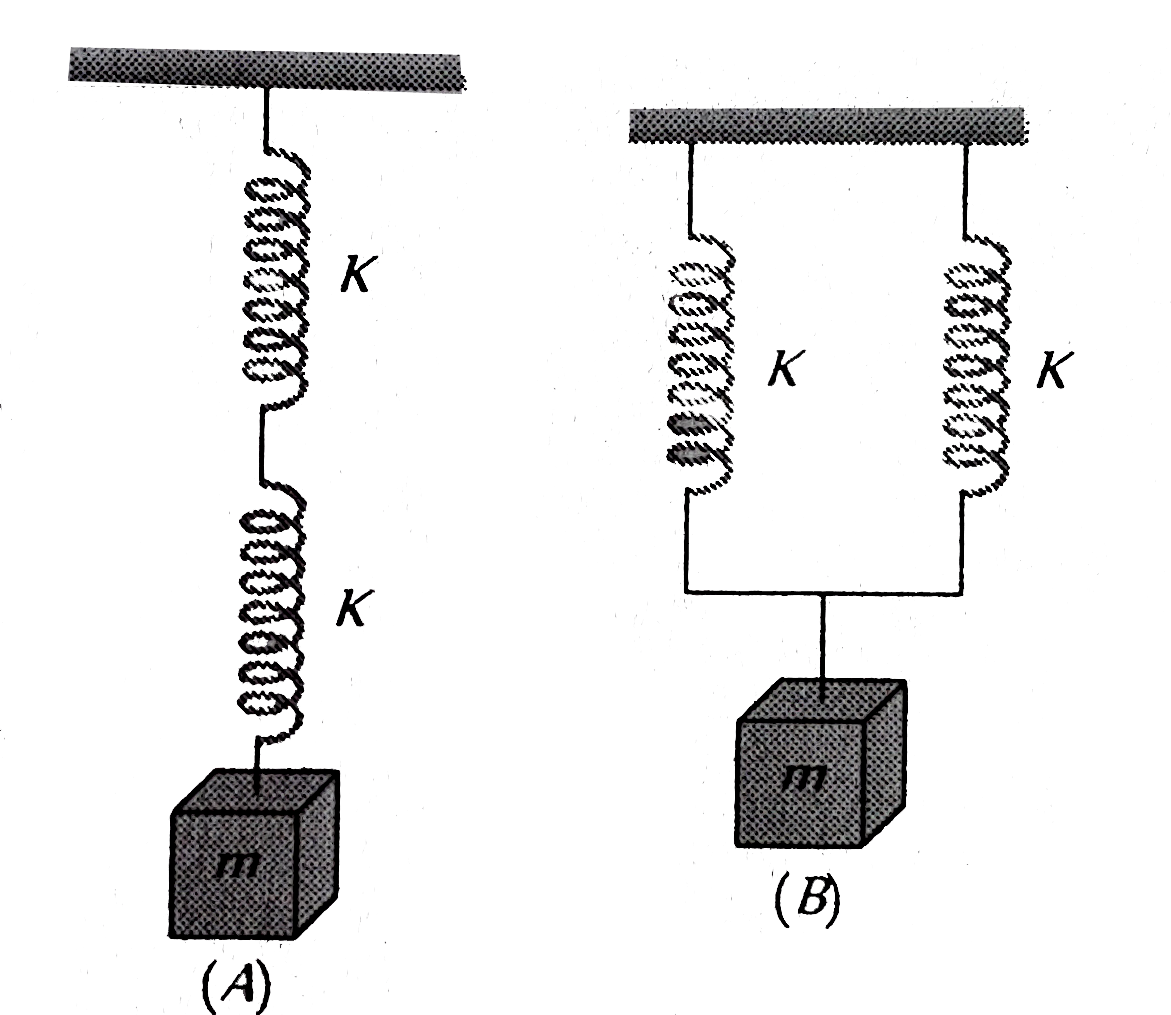 Solution in Gujrati
Solution in Gujrati
2:1
1:1
1:2
4:1
The correct Answer is:C
Step by step video & image solution for Two identical spring of constant K are connected in series and parallel as shown in figure. A mass is suspended from them. The ratio of their frequencies of vertical oscillations will be by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Oscillations) (Simple pendulum and types of SHM)
17 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Fundamental)
24 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Dscillations) (Kinematics of SHM)
20 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLEN CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
Similar Questions
Two pendulums of length 1.21 m and 1.0 m starts vibrationg. At some instant, the two are in the mean position in same phase. After how many vibrations of the longer pendulum, the two will be in phase ?
View SolutionLet speed of sound waves in hydrogen gas at room temperature is v0. What will be the speed of sound waves in a room which contains an equimolar mixture of hydrogen and 'He' at same temperature :-
View SolutionTwo particles executing SHM of same frequency meet at x=+√3A2, while moving in opposite directions. Phase difference between the particles is :-
View SolutionAssertion: The driver in a vechicle moving with a constant speed on a straight road is in a non-inertial frame of referance.
Reason: A reference frame in which Newton's laws of motion are applicable is non-inertial.
View SolutionA rod with rectangular cross section oscillates about a horizontal axis passing through one of its ends and it behaves like a seconds pendulum, its length will be
View SolutionTwo identical springs, each of force constant k are connected I (a) series (b) parallel and they support a mass M. Calculate the ratio of the frequency of oscillation of the mass in two systems.
View SolutionFind the ratio of the periods of two identical springs if they are first joined in series & then in parallel & a mass m is suspended from them:
View SolutionTwo identical springs of spring constant k each are connected in series and parallel as shown in figure. A mass M is suspended from them. The ratio of their frequencies of vertical oscillation will be
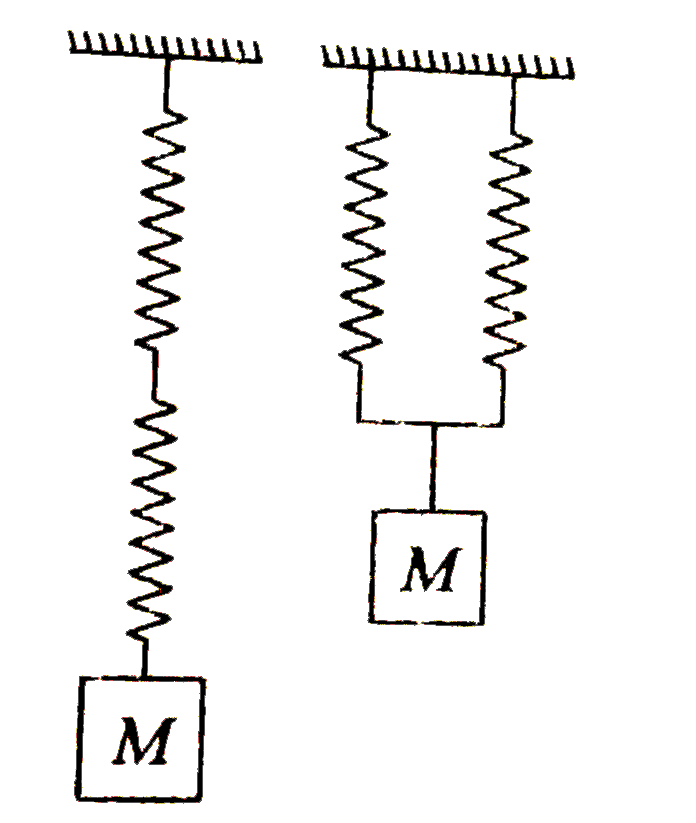
View SolutionSome springs are combined in series and parallel arrangement as shown in the figure and a mass m is suspended from them. The ratio of their frequencies will be
View SolutionSome springs are combined in series and parallel arrangement as shown in the figure and a mass m is suspended from them. The ratio of their frequencies will be :-
_E01_040_Q01.png)
View SolutionThe frequency of oscillations of a mass m connected horizontally by a spring of spring constant k is 4 HZ. When the spring is replaced by two identical spring as shown in figure. Then the effective frequency is
View SolutionTwo identical springs each of force constant k are connected in series Calculate the frequency of the system
View SolutionTwo identical springs each of force constant k are connected in parallel and they support a mass mu . Calculate the ratio of the frequency of oscillation of the mass in two systems.
View SolutionTwo identical springs each of force constant k are connected in parallel and they support a mass mu . Calculate the ratio of the frequency of oscillation of the mass in two systems.
View SolutionTwo spring of force constants k and 2k are connected to a mass as shown in figure. The frequency of oscillation of the mass is……..

View SolutionTwo identical springs of spring constant k each are connected in series and parallel as shown in figure. A mass M is suspended from them. The ratio of their frequencies of vertical oscillation will be
View Solution
