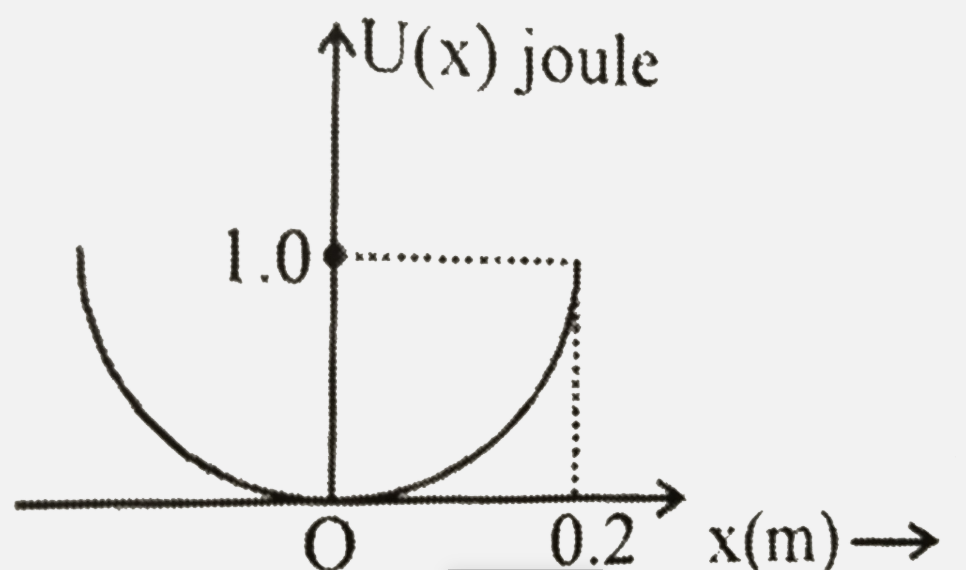
A particle of mass 4kg moves simple harmonically such that its PE (U) varies with position x, as shown. The period of oscillations is :-
 Solution in Gujrati
Solution in Gujrati
2π25s
π√25
4π5s
2π√25s
The correct Answer is:D
Step by step video & image solution for A particle of mass 4kg moves simple harmonically such that its PE (U) varies with position x, as shown. The period of oscillations is :- by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Oscillations) (Simple pendulum and types of SHM)
17 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Fundamental)
24 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Dscillations) (Kinematics of SHM)
20 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLEN CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
Similar Questions
Two pendulums of length 1.21 m and 1.0 m starts vibrationg. At some instant, the two are in the mean position in same phase. After how many vibrations of the longer pendulum, the two will be in phase ?
View SolutionLet speed of sound waves in hydrogen gas at room temperature is v0. What will be the speed of sound waves in a room which contains an equimolar mixture of hydrogen and 'He' at same temperature :-
View SolutionTwo particles executing SHM of same frequency meet at x=+√3A2, while moving in opposite directions. Phase difference between the particles is :-
View SolutionAssertion: The driver in a vechicle moving with a constant speed on a straight road is in a non-inertial frame of referance.
Reason: A reference frame in which Newton's laws of motion are applicable is non-inertial.
View SolutionA rod with rectangular cross section oscillates about a horizontal axis passing through one of its ends and it behaves like a seconds pendulum, its length will be
View SolutionA particle of mass 2 kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is
View SolutionWhen a particle oscillates simple harmonically, its potential energy varies periodically. If the frequency of oscillation of the particle is n, the frequency of potential energy variation is
View SolutionThe variation of potential energy (U) of a simple harmonic oscillator is as shown. Then force constant of the system is (PE is in joules, displacement 'x' is in mm)
View SolutionA particle of mass = 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is (npi)/5 second. Find value of n.
View SolutionA particle of mass 4kg moves simple harmonically such that its PE (U) varies with position x, as shown. The period of oscillations is :-

View SolutionWhen a particle oscillates simple harmonically, its kinetic energy varies periodically. If frequency of the particle is n, the frequency of the kinetic energy is
View SolutionThe PE of a simple harmonic oscillator 0.1 s after crossing the mean position is 1/4 of its total energy. Then the period of its oscillation is
View SolutionThe variations of potential energy (U) with position x for three simple harmonic oscillators A, B and C are shown in figure. The oscillators have same mass. The time period of oscillation is greatest for
View SolutionWhen a particle oscillates simple harmonically, its potential energy varies periodically. If the frequency of oscillation of the particle is n, the frequency of potential energy variation is………………
View SolutionThe variation of PE of a simple harmonic oscillator is as shown. Then force constant of the system is (PE 'U' is in joules, displacement 'x' is in mm)

View SolutionIf the displacement of a simple harmonic oscillators is half of its amplitude at an instant. PE of the oscillator is
View Solution
