A glass sphere of index 1.5 and radius 40 cm has half its hemispherical surface silvered.
The point where a parallel beam of light, coming along a diameter, will focus (or appear to) after coming out of sphere, will be :
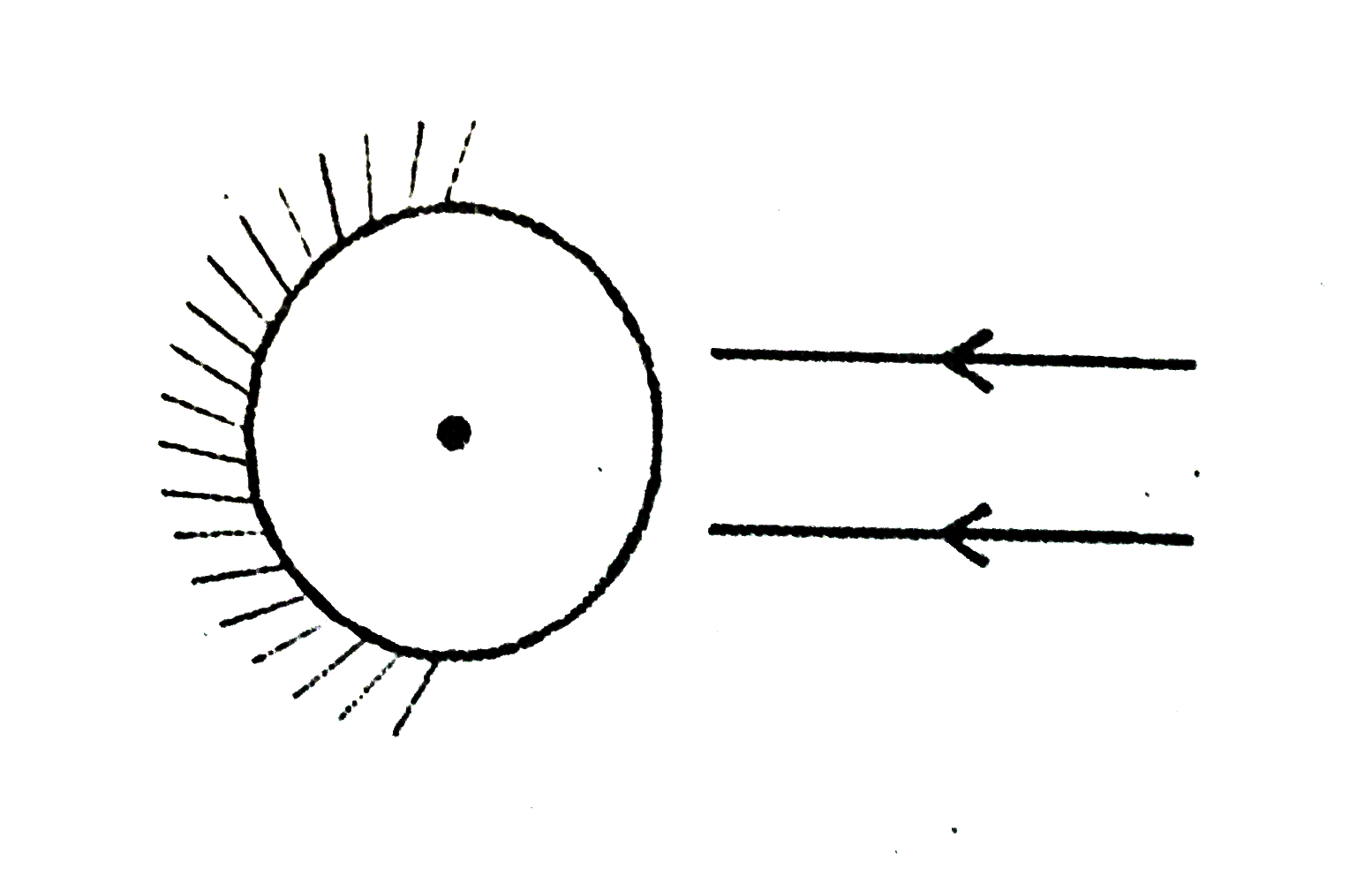
10 cm to the left of centre
30 cm to the left of centre
50 cm to the left of centre
60 cm to the left of centre
The correct Answer is:D
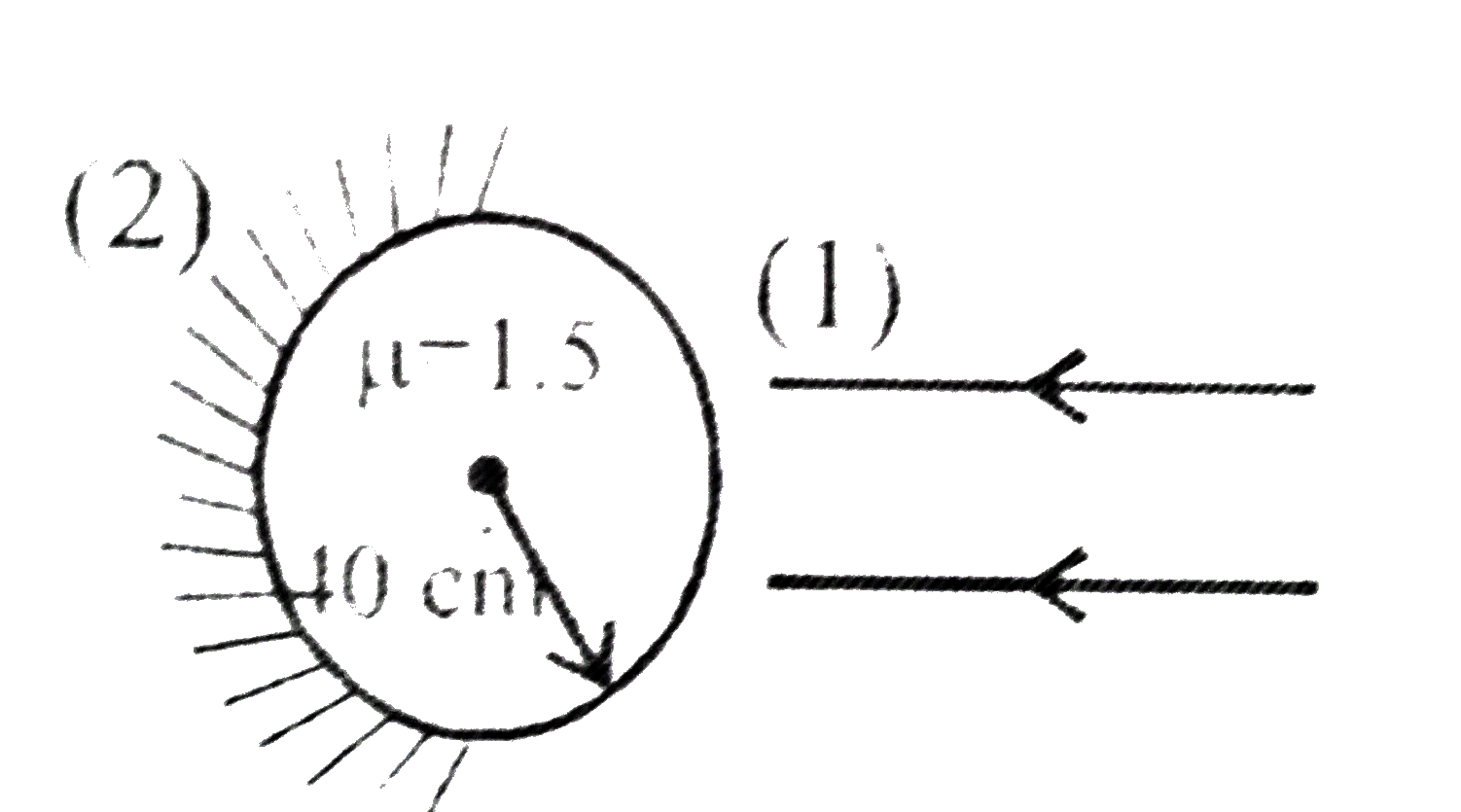
For refracting surface
cm
for mirror
for refracting surface ...(i)
cm
So the distance of image frosm the centre e will be 100 - 40 = 60 cm (left of the centre )
Topper's Solved these Questions
Similar Questions
A glass sphere, refractive index 1.5 and radius 10cm, has a spherical cavity of radius 5cm concentric with it. A narrow beam of parallel light is directed into the sphere. Find the final image and its nature.

View SolutionA clear transparent glass sphere (μ=1.5) of radius R is immersed in a liquid of refractive index 1.25. A parallel beam of light incident on it will converge to a point. The distance of this point from the center will be
View Solution
Knowledge Check
A glass sphere, refractive index 1.5 and radius 10cm, has a spherical cavity of radius 5cm concentric with it. A narrow beam of parallel light is directed into the sphere. Find the final image and its nature.
 A25cm left of S4, virtualB25 cm right of S4 , realC15 cm left of S4, virtualD20cm right of S4, virtual
A25cm left of S4, virtualB25 cm right of S4 , realC15 cm left of S4, virtualD20cm right of S4, virtualA clear transparent glass sphere (μ=1.5) of radius R is immersed in a liquid of refractive index 1.25. A parallel beam of light incident on it will converge to a point. The distance of this point from the center will be
A−3RB+3RC−RD+R
A glass sphere of radius 15 cm has a small bubble 6 cm from its centre. The bubble is viewed along a diameter of the sphere from the side on which it lies. How for from the surface will it appear to be if the refractive index of glass is 1.5 ?
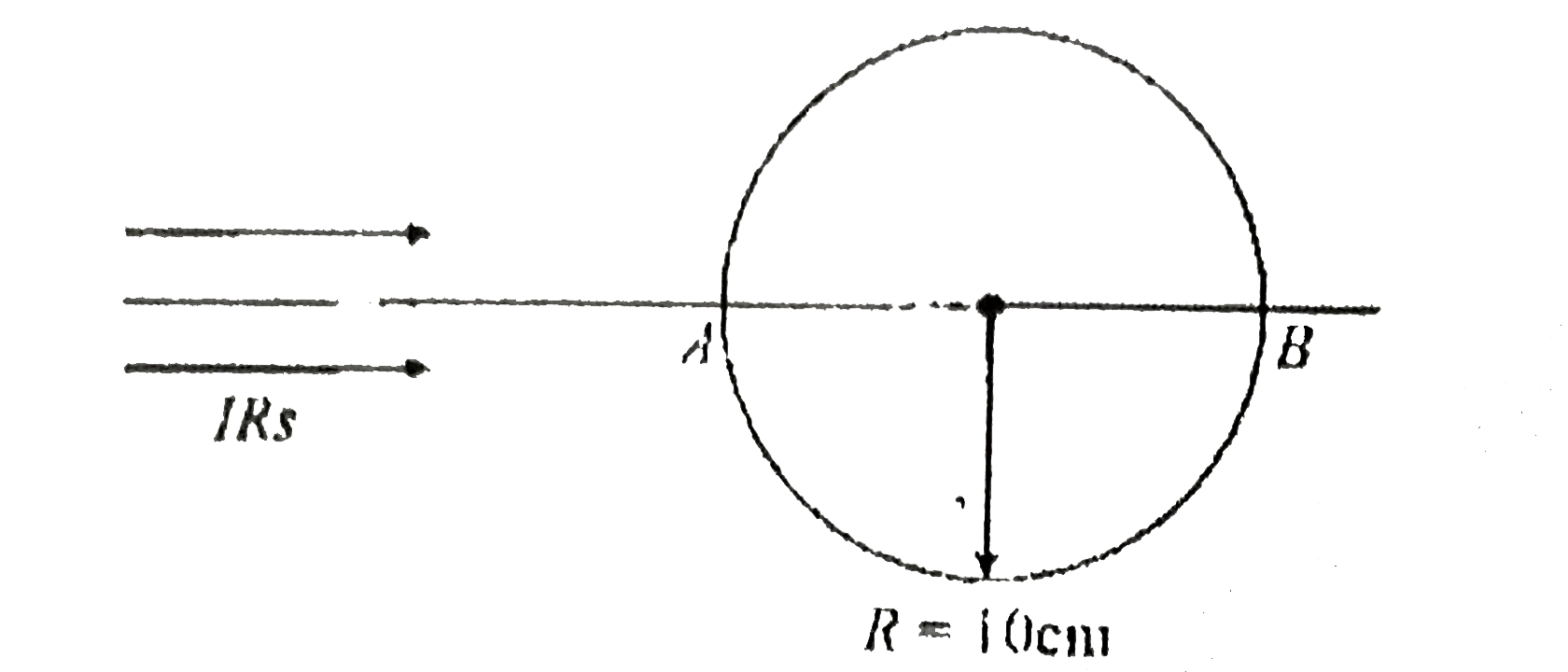
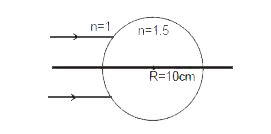
View SolutionFigure shows a glass sphere of radius 10 cm. along its diameter AB from one side a parallel beam of paraxial rays incident on it. What should be the refractive index of glass so that after refraction all rays will converge at opposite end B.
View SolutionA glass sphere of (μ=1.5) with a radius of 15.0cm has a tiny air bubble 5cm above its centre. The sphere is viewed looking down along the extended radius containing the bubble. What is the apparent depth of the bubble below the surface of the sphere?
View SolutionA glass sphere of (μ=1.5) with a radius of 15.0cm has a tiny air bubble 5cm above its centre. The sphere is viewed looking down along the extended radius containing the bubble. What is the apparent depth of the bubble below the surface of the sphere?
View SolutionFindout the position where parallel rays will meet after coming out of the sphere and draw the appropriate ray diagram
View SolutionA glass sphere (μ=1.5) of radius 20 cm has a small air bubble 4 cm below its centre. The sphere is viewed from outside and along a vertical line through the bubble. The apparent depth of the bubble below the surface of sphere is (in cm)
View Solution
