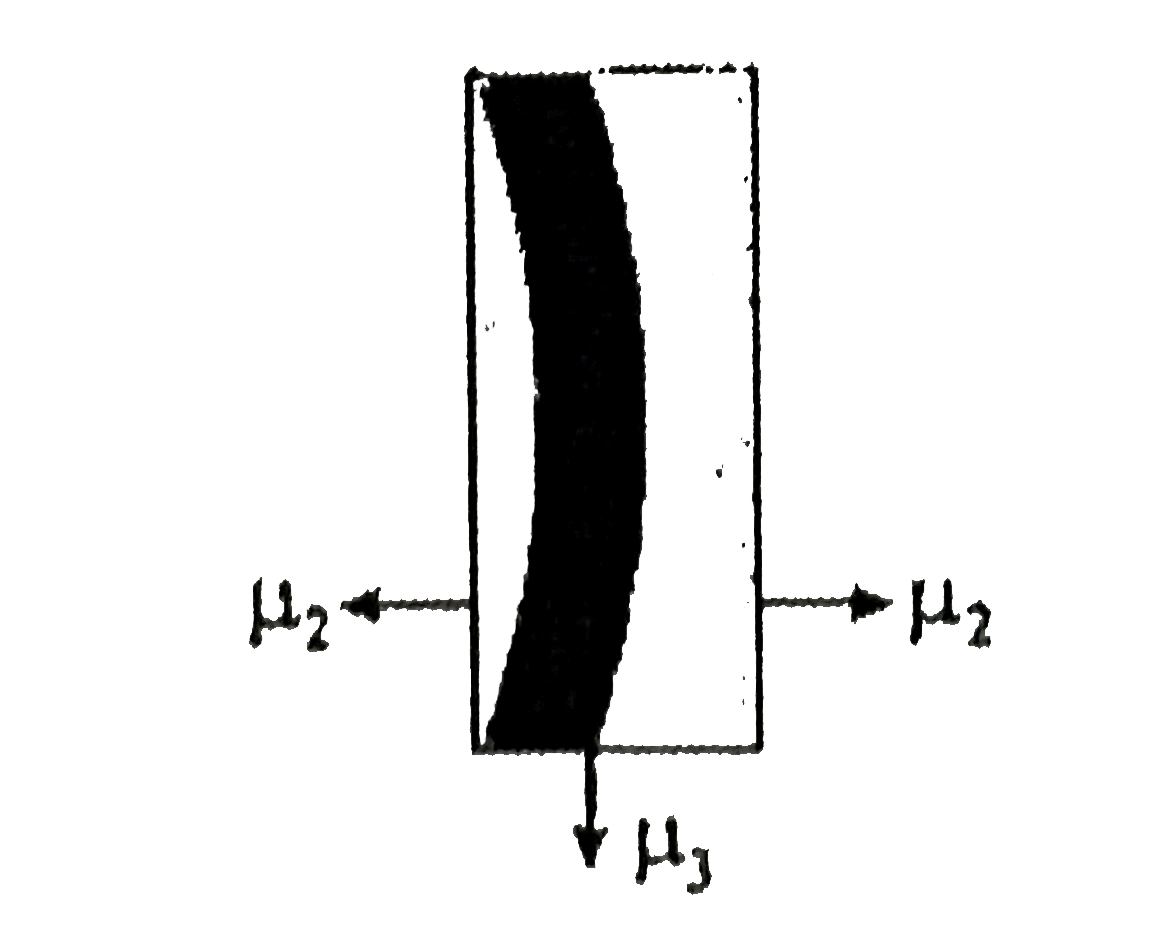
The adjacent figure shows a thin plano-convex lens of refractive index μ1 and a thin plano-concave lens of refractive index μ2, both having same radius of curvature R of their curved surfaces. The thin lens of refractive index μ3 has radius of curvature R of both its surfaces. This lens is so placed in between the plano-convex and plano-concave lenses that the plane surfaces are parallel to each other.
The focal length of the combination is
 Solution in Gujrati
Solution in Gujrati
R(μ1+μ2−μ3−1)
R(μ1+μ2+μ3)
R(μ1−μ2)
R(μ1−μ2−μ3−3)
The correct Answer is:C
1f1=(μ1−1)(1∞+1R)=μ1−1R
⇒1f1=(μ3−1)(−1R+1R)=0
1f3=(μ2−1)(−1R−1∞)=−(μ2−1)R
1f=1f1+1f2+1f3=(μ1−1)R−(μ2−1)R−1R(μ1−μ2)
⇒f=R(μ1−μ2)
Topper's Solved these Questions
Similar Questions
Find dydx for the following :
(i) y=x7/2 (ii) y=x−3
(iii)y=x (iv) y=x5+x3+4x1/2+7
(v) y=5x4+6x3/2+9x (vi) y=ax2+bx+C
(Vii)y=3x^(5)-3x-1/x
View SolutionThe radius of curvature of curved surface of a thin plano-convex lens is 10 cm and the refractive index is 1.5 . If the plano surface is silvered, then the focal length will be.
View SolutionThe radius of curvature of the convex surface of a thin plano-convex lens is 15 cm and the refractive index of its material is 1.6. The power of the lens is
View SolutionA thin plano-convex lens fits exactly into a thin plano-concave lens. Their plane surfaces are parallel to each other. The lenses are made of different material of refractive indices mu_(1) and mu_(2) and R is the radius of curvature of the curved surfaces of the lenses, if rays are incident parallel to principal axis on lens of refractive index.
View SolutionThe figure below shows a thin plano-convex lens of refractive index μ1 and a thin plano-concave lens of refractive index μ2, both having same radius of curvature R of their curved surfaces. Another thin lens of refractive index μ3 has same radius of curvature R on the two surface between the plano-convex and plano-concae lenses that the plane surfaces are parallel to each other. Find the focal length of the combination.
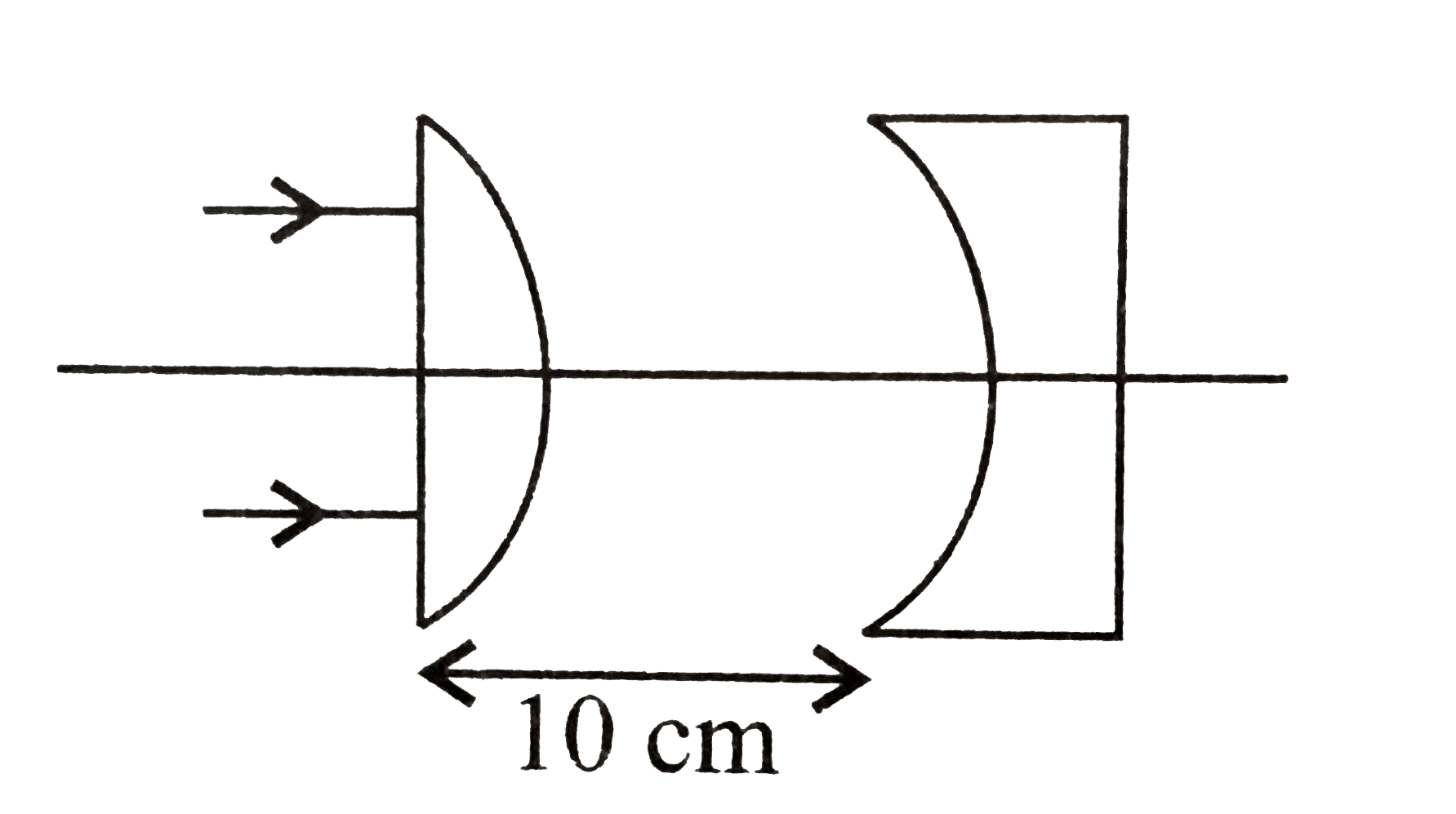
View SolutionIn the given figure, the radius of curvature of curved surface for both the plano-convex and plano-concave lens is 10 cm and refractive index for both is 1.5 . The location of the final image after all the refractions through lenses is
View SolutionA plano-convex lens (focal length f2, refractive indexμ2, radius of curvature R) fits exactly into a plano-concave lens (focal lengthf1 refractive index μ1, radius of curvature R). Their plane surfaces are parallel to each other. Then, the focal length of the combination will be :
View SolutionA plano-convex lens (focal length f_2 , refractive index mu_(2) , radius of curvature R) fits exactly into a plano-concave lens (focal length f_(1) refractive index mu_1 , radius of curvature R). Their plane surfaces are parallel to each other. Then, the focal length of the combination will be :
View SolutionThe radius of curvature of the convex surface of a thin plano-convex lens is 12 cm, and the refractive index of its material is 1.6. What is the power of lens ?
View SolutionFind the focal length of plano convex lens, when its radius of curvature of the surface is R and n is the refractive index of the lens?
View SolutionA thin plano-convex lens acts like a concave mirror of focal length 0.2 m when silvered from its plane surface. The refractive index of the material of the lens is 1.5. The radius of curvature of the convex surface of the lens will be
View SolutionA plano-convex lens (focal length f2, refractive indexμ2, radius of curvature R) fits exactly into a plano-concave lens (focal lengthf1 refractive index μ1, radius of curvature R). Their plane surfaces are parallel to each other. Then, the focal length of the combination will be :
View SolutionIn the given figure, the radius of curvature of curved surface for both the plano-convex and plano-concave lens is 10 cm and refractive index for both is 1.5. The location of the final image after all the refractions through lenses is
View SolutionIf the plane surface of a plano-convex lens of radius of curvature R and refractive index mu is silvered, then its focal length would be
View SolutionA thin plano-convex lens acts like a concave mirror of focal length 0.2 m when silvered from its plane surface. The refractive index of the material of the lens is 1.5. The radius of curvature of the convex surface of the lens will be
View SolutionThe radius of curvature of the convex surface of a thin plano-convex lens is 12 cm, and the refractive index of its material is 1.6. What is the power of lens ?
View Solution
