The graph between wave number (→v) and angular frequency (ω) is
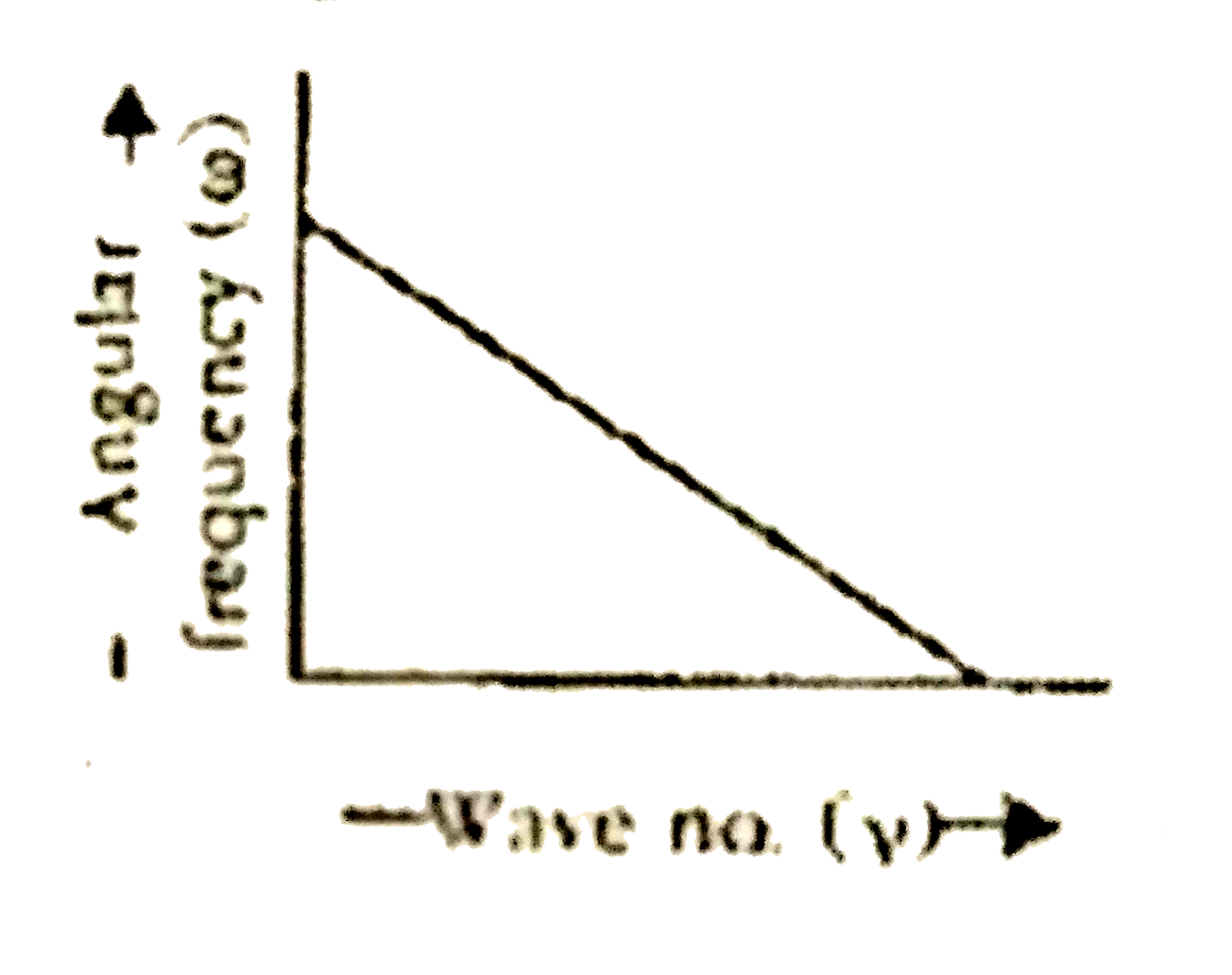
The correct Answer is:A
To solve the problem of finding the graph between wave number (v) and angular frequency (ω), we can follow these steps:
1. Understand the Relationship:
We start with the basic wave equation which relates the speed of a wave (C), frequency (f), and wavelength (λ):
C=f⋅λ
2. Express Wavelength in Terms of Wave Number:
The wave number (v) is defined as the reciprocal of the wavelength:
v=1λ⟹λ=1v
3. Express Frequency in Terms of Angular Frequency:
The frequency (f) can be expressed in terms of angular frequency (ω):
f=ω2π
4. Substitute into the Wave Equation:
Now, substitute the expressions for λ and f into the wave equation:
C=(ω2π)⋅(1v)
5. Rearranging the Equation:
Rearranging the equation gives:
C=ω2πv
Multiplying both sides by 2πv leads to:
ω=2πCv
6. Identify the Linear Relationship:
The equation ω=2πCv shows that ω is directly proportional to v. This can be written in the form of a linear equation:
y=mx
where y=ω, x=v, and m=2πC.
7. Graph Interpretation:
The graph of this relationship will be a straight line passing through the origin, with the slope equal to 2πC. The y-axis represents angular frequency (ω) and the x-axis represents wave number (v).
Conclusion:
The graph between wave number (v) and angular frequency (ω) is a straight line passing through the origin, indicating a linear relationship.
---
We start with the basic wave equation which relates the speed of a wave (C), frequency (f), and wavelength (λ):
C=f⋅λ
The wave number (v) is defined as the reciprocal of the wavelength:
v=1λ⟹λ=1v
The frequency (f) can be expressed in terms of angular frequency (ω):
f=ω2π
Now, substitute the expressions for λ and f into the wave equation:
C=(ω2π)⋅(1v)
Rearranging the equation gives:
C=ω2πv
Multiplying both sides by 2πv leads to:
ω=2πCv
The equation ω=2πCv shows that ω is directly proportional to v. This can be written in the form of a linear equation:
y=mx
where y=ω, x=v, and m=2πC.
The graph of this relationship will be a straight line passing through the origin, with the slope equal to 2πC. The y-axis represents angular frequency (ω) and the x-axis represents wave number (v).
The graph between wave number (v) and angular frequency (ω) is a straight line passing through the origin, indicating a linear relationship.
Similar Questions
The graph between the angular momentum J and angular velocity ω will be :-
View SolutionA sinusoidal wave travelling in the positive x-direction has an amplitude of 15.0cm, a wavelength of 40.0cm and a frequency of 8.00Hz.Thevertic≤displacementofthemediumatt = 0 and x = 0isalso15.0 cmasshown∈figure.<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/DCP_V03_C17_E01_054_Q01.pngwh=80%mx-autosty≤=background:white;><br>(a)F∈dtheanga––rwaveνmberk,periodT,anga––requencyomegaandspeedv of the wave.
(b) Write a general expression for wave function.
View Solution
Knowledge Check
A particle of mass m executing SHM with amplitude A and angular frequency ω. The average value of the kinetic energy and potential energy over a period is
A0,12mω2A2B12mω2A2,0C12mω2A2,12mω2A2D14mω2A2,14mω2A2
What is the time period of a wave having angular frequency (ω) equal to 0.5s−1?
View SolutionThe relation between wavelength (λ) and angular wave number (k) of a wave is
View SolutionWhich of the following does not have the dimensions of velocity ? ( Given ε0 is the permittivity of free space , μ0 is the permeability of free space , v is frequency , λ is wavelength , P is the pressure , and ρ is density , k is wave number , ω is the the angular frequency) (1)ω k (2)vλ (3)1/√ε0μ0 (4)√Pρ
View SolutionA square loop of side b is rotated in a constant magnetic field B at angular frequency ω as shown in the figure. What is the emf induced in it?
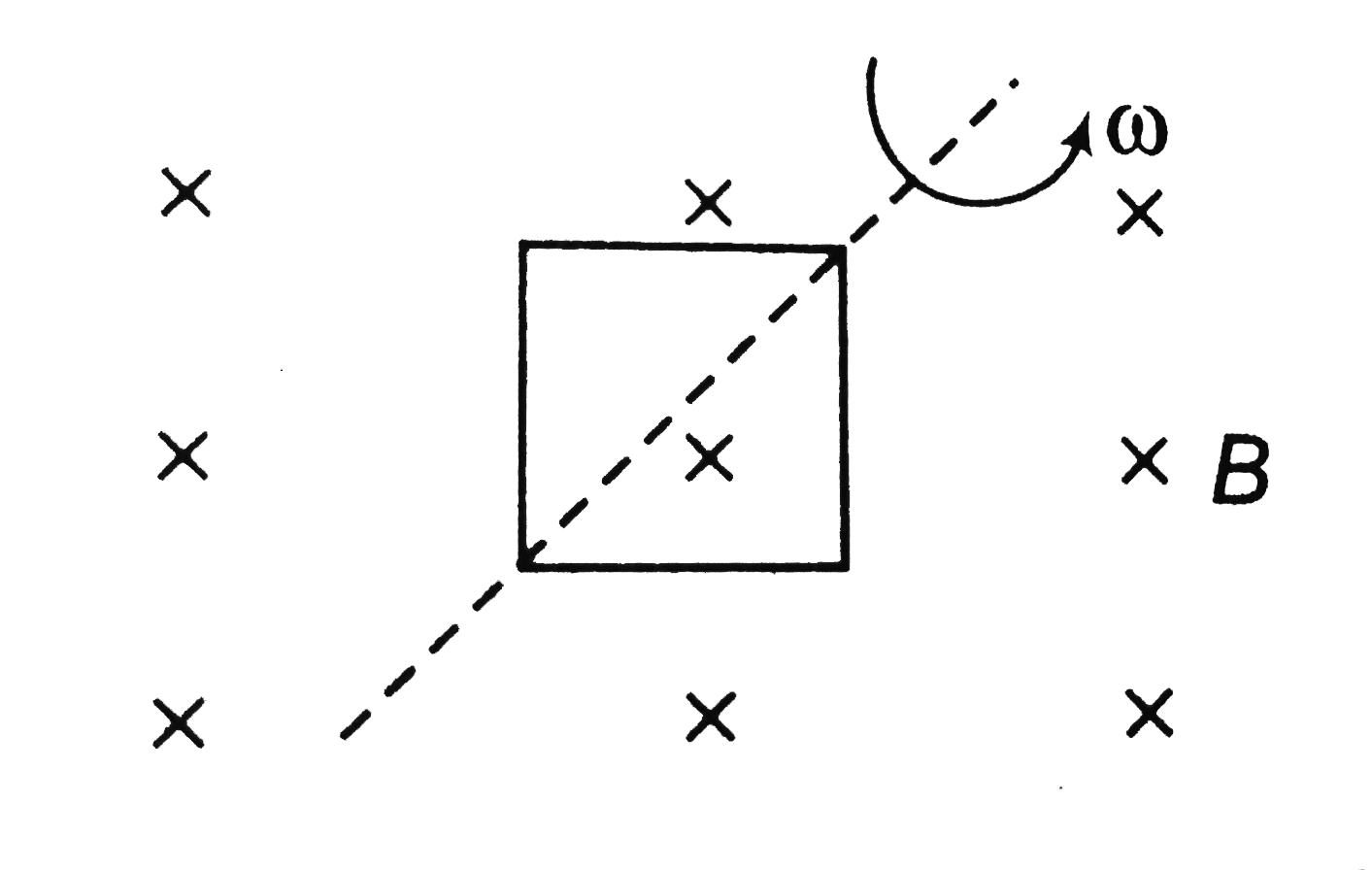
View SolutionThe work functions of three metals A, B and C are WA,WBandWC respectively . They are in decreasing order. The correct graph between kinetic energy and frequency V of incident radiation is
View SolutionA constant power is suppied to a rotating disc. The relationship between the angular velocity (ω) of the disc and number of rotations (n) made by the disc is governed by
View SolutionThe graph between the square root of the frequency of a specific line of characteristic spectrum of X - rays and the atomic number of the target will be
View Solution
