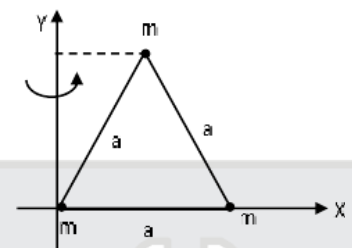
Side of an equilateral triangle is I . Three point masses, each of magnitude m, are palced at the three vertices of the triangle . Momment of inertia of this system about one side of the triangle as axis is given by
3ml24
43mt2
32ml2
23ml2
The correct Answer is:A
To find the moment of inertia of a system of three point masses placed at the vertices of an equilateral triangle about one of its sides, we can follow these steps:
1. Understand the Configuration:
- We have an equilateral triangle with side length L.
- Three point masses, each of mass m, are placed at the vertices of the triangle.
2. Identify the Axis of Rotation:
- The axis of rotation is along one of the sides of the triangle. Let's denote the vertices of the triangle as A, B, and C with the side AB being the axis.
3. Calculate the Moment of Inertia for Each Mass:
- The moment of inertia I about an axis is given by the formula:
I=∑mir2i
- Where mi is the mass and ri is the distance from the axis of rotation.
4. Calculate for Mass at Vertex A and B:
- The masses at vertices A and B are on the axis of rotation. Therefore, their distances from the axis are zero:
IA=m⋅02=0
IB=m⋅02=0
5. Calculate for Mass at Vertex C:
- The distance of mass m at vertex C from the axis AB can be calculated using the height of the triangle. The height h of an equilateral triangle is given by:
h=√32L
- The distance from the side AB to vertex C is h:
rC=h=√32L
- Therefore, the moment of inertia for mass C is:
IC=m⋅(√32L)2=m⋅34L2
6. Total Moment of Inertia:
- Now, we can sum up the moments of inertia:
Itotal=IA+IB+IC=0+0+m⋅34L2=34mL2
Final Result:
The moment of inertia of the system about one side of the triangle is:
I=34mL2
- We have an equilateral triangle with side length L.
- Three point masses, each of mass m, are placed at the vertices of the triangle.
- The axis of rotation is along one of the sides of the triangle. Let's denote the vertices of the triangle as A, B, and C with the side AB being the axis.
- The moment of inertia I about an axis is given by the formula:
I=∑mir2i
- Where mi is the mass and ri is the distance from the axis of rotation.
- The masses at vertices A and B are on the axis of rotation. Therefore, their distances from the axis are zero:
IA=m⋅02=0
IB=m⋅02=0
- The distance of mass m at vertex C from the axis AB can be calculated using the height of the triangle. The height h of an equilateral triangle is given by:
h=√32L
- The distance from the side AB to vertex C is h:
rC=h=√32L
- Therefore, the moment of inertia for mass C is:
IC=m⋅(√32L)2=m⋅34L2
- Now, we can sum up the moments of inertia:
Itotal=IA+IB+IC=0+0+m⋅34L2=34mL2
The moment of inertia of the system about one side of the triangle is:
I=34mL2
Similar Questions
Knowledge Check
Three point masses each of mass m are placed at the corners of an equilateral triangle of side b. The moment of inertia of the system about an axis coinciding with one side of the triangle is
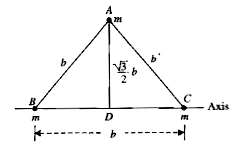 A3mb2Bmb2C(3/4)mb2D(2/3)mb2
A3mb2Bmb2C(3/4)mb2D(2/3)mb2Three masses each of mass m are palced at the vertices of an equilateral triangles ABC of side l as shown in figure. The force acting on a mass 2m placed at the centroid O of the triangle is
 AzeroB3Gm2l2C5Gm2l2D7Gm2l2
AzeroB3Gm2l2C5Gm2l2D7Gm2l2
Each side of an equilateral triangle measure 10 cm. Find the area of the triangle .
View SolutionThree point masses m1,m2 and m3 are located at the vertices of an equilateral triangle of side α. What is the moment of inertia of the system about an axis along the altitude of the triangle passing through m1?
View SolutionThree point masses m1,m2 and m3 are located at the vertices of an equilateral triangle of side α. What is the moment of inertia of the system about an axis along the altitude of the triangle passing through m1?
View SolutionThree identical rods, each of mass m and length l, form an equaliteral triangle. Moment of inertia about one of the sides is

View SolutionConstruct an equilateral triangle of sides 6 cm each.
View SolutionThree point charges q are placed at three vertices of an equilateral triangle of side a. Find magnitude of electric force on any charge due to the other two.
View Solution