Which of the following graph depicts spring constant k versus length l of the spring correctly
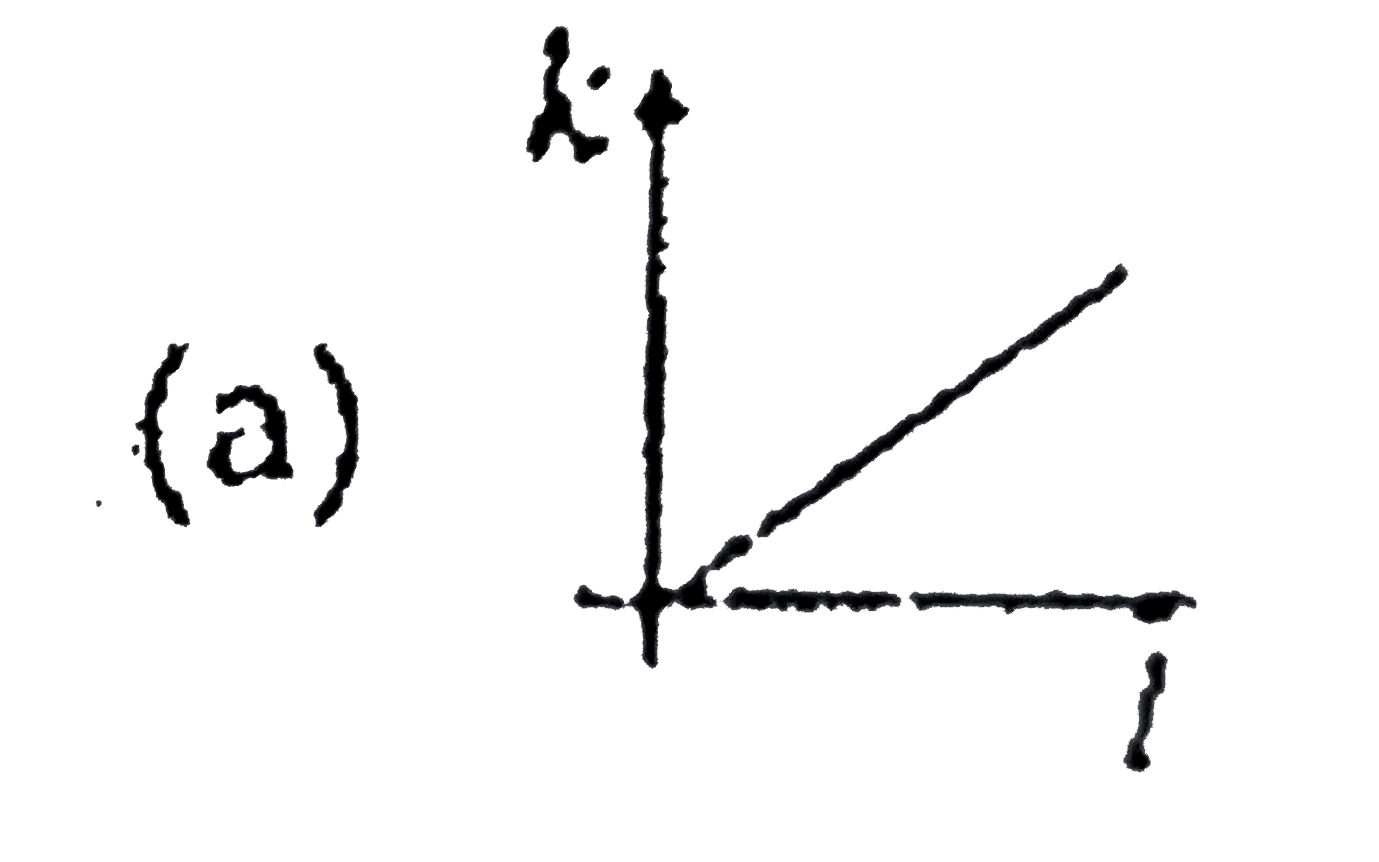

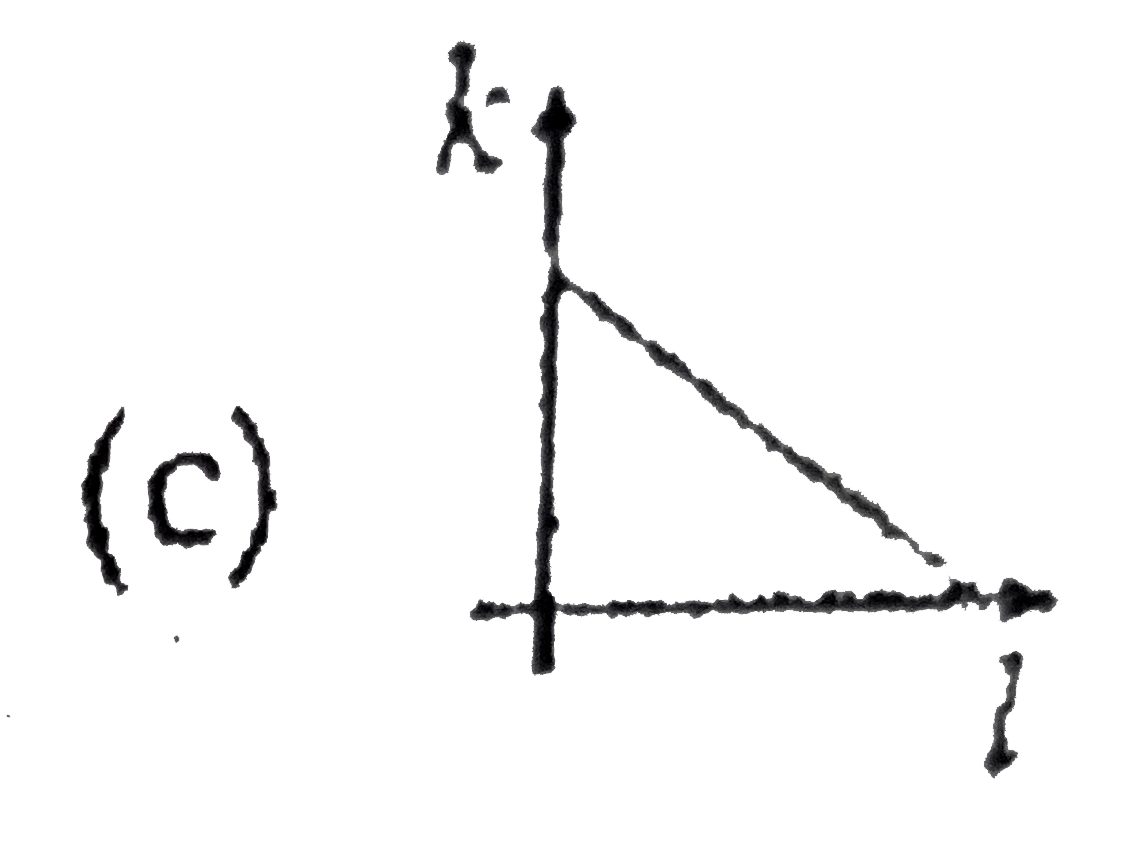
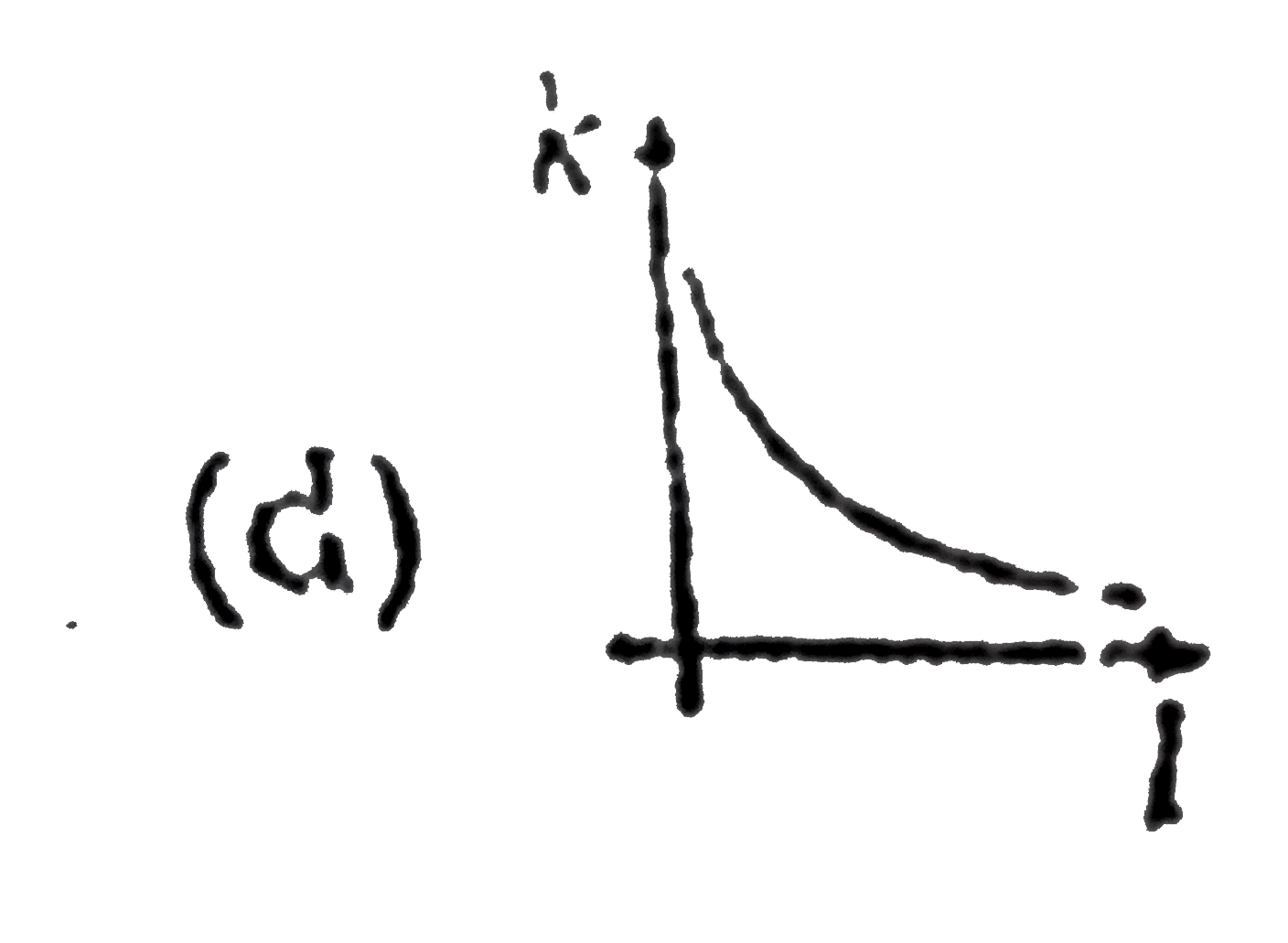
The correct Answer is:D
To solve the problem of determining which graph correctly depicts the relationship between the spring constant k and the length l of the spring, we can follow these steps:
1. Understand the Spring Constant: The spring constant k is defined by Hooke's Law, which states that the force F exerted by a spring is proportional to the displacement x from its equilibrium position:
F=−kx
Here, k is the spring constant, and x is the extension or compression of the spring.
2. Relationship Between Force and Spring Constant: Rearranging Hooke's Law gives us:
k=Fx
This indicates that the spring constant k is dependent on the force applied and the displacement of the spring.
3. Consider the Effect of Length on Spring Constant: When we consider a spring of length l, if we increase the length of the spring while keeping the force F constant, the displacement x will increase. This implies that:
k=Fx
As x increases (due to increased length), k decreases.
4. Establish the Inverse Relationship: From the above reasoning, we can conclude that:
k∝1l
This means that as the length l of the spring increases, the spring constant k decreases. This is an inverse relationship.
5. Graphical Representation: The relationship k∝1l can be represented graphically as a hyperbola. In a graph of k versus l:
- As l increases, k decreases.
- The graph will approach the axes but never touch them, which is characteristic of a hyperbolic curve.
6. Identify the Correct Graph: Given the options, we need to identify which graph represents this inverse relationship. The correct graph should be a hyperbola, which shows that as the length l increases, the spring constant k decreases.
Conclusion:
Based on the analysis, the correct option is Option D, which depicts the relationship between the spring constant k and the length l of the spring as a hyperbola.
F=−kx
Here, k is the spring constant, and x is the extension or compression of the spring.
k=Fx
This indicates that the spring constant k is dependent on the force applied and the displacement of the spring.
k=Fx
As x increases (due to increased length), k decreases.
k∝1l
This means that as the length l of the spring increases, the spring constant k decreases. This is an inverse relationship.
- As l increases, k decreases.
- The graph will approach the axes but never touch them, which is characteristic of a hyperbolic curve.
Based on the analysis, the correct option is Option D, which depicts the relationship between the spring constant k and the length l of the spring as a hyperbola.
Similar Questions
The electrical analog of a spring constant k is
View SolutionA fixed container is fitted with a piston which is attached to a spring of spring constant k. The other and of the spring is attached to a rigid wall. Initially the spring is in its natural length and the length of container between the piston and its side wall is L. Now an dideal diatomic gas is slowly filled in the container so that the piston moves quasistatically. It pushed the piston by x so that the spring now is compressed by x. The total rotaional kinetic energy of the gas molecules in terms of the displacement x of the piston is (there is vacuum outside the container)
View SolutionThe time period (T) of a spring mass system depends upon mass (m) & spring constant (k) & length of the spring (l)[k=Forcelength]. Find the relation among T, m , l & k using dimensional method.
View SolutionA constant voltage at different frequencies is applied across a capacitance. C as shown in the figure. Which of the following graphs correctly depicts the varitaion of current with frequency?

View SolutionA spring of certain length and having spring constant k is cut into two pieces of length in a ratio 1:2. The spring constants of the two pieces are in a ratio :
View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View SolutionTwo equal masses are attached to the two ends of a spring of spring constant k. The masses are pulled out symmetrically to stretch the spring by a length x over its natural length. The work done by the spring one each mass is
View SolutionA body of mass m is attached by an inelastic string to a suspended spring of spring constant k. Both the string and the spring have negligible mass and the string is inextensible and of length L. Initially, the mass m is at rest.
The largest amplitude Amax, for which the string will remain taut throughout the motion is
View SolutionThe frequency of oscillations of a mass m connected horizontally by a spring of spring constant k is 4 HZ. When the spring is replaced by two identical spring as shown in figure. Then the effective frequency is

View SolutionA spring is attached with a block of mass m and a fixed horizontal roof as shown. The block is lying on a smooth horizontal table and initially the spring is vertical and unstretched. Natural length of spring is 3l0. A constant horizontal force F is applied on the block so that block moves in the direction of force. When length of the spring becomes 5l0, block leaves contact with the table. Find the constant force F, if initial and final velocity of block is zero.
View Solution
