The electrical analog of a spring constant k is
L
R
C
1C
The correct Answer is:D
To find the electrical analog of a spring constant k, we can analyze the behavior of an LC circuit (which consists of an inductor L and a capacitor C) and compare it to the mechanics of a spring.
1. Understanding the LC Circuit:
- In an LC circuit, we have an inductor (L) and a capacitor (C) connected in parallel. The capacitor stores electrical energy in the form of an electric field, while the inductor stores energy in the form of a magnetic field.
2. Setting Up the Equations:
- Let's denote the charge on the capacitor as Q and the current through the inductor as I. The potential across the capacitor is given by:
VC=QC
- The back EMF (electromotive force) across the inductor is given by:
VL=−LdIdt
3. Relating Charge and Current:
- Since the capacitor is discharging, we can express the current I as:
I=−dQdt
- Substituting this into the equation for the inductor gives:
VL=−Lddt(−dQdt)=Ld2Qdt2
4. Equating the Potentials:
- Since the capacitor and inductor are in parallel, their potentials are equal:
QC=Ld2Qdt2
5. Rearranging the Equation:
- Rearranging gives us:
Ld2Qdt2+QC=0
- This resembles the equation of motion for simple harmonic motion (SHM), which is:
md2xdt2+kx=0
6. Identifying Analogies:
- In SHM, m is the mass and k is the spring constant. In our electrical analogy:
- The electrical analog of mass m is the inductor L.
- The electrical analog of the spring constant k is 1C.
7. Conclusion:
- Therefore, the electrical analog of the spring constant k is:
k=1C
Final Answer:
The electrical analog of a spring constant k is 1C.
- In an LC circuit, we have an inductor (L) and a capacitor (C) connected in parallel. The capacitor stores electrical energy in the form of an electric field, while the inductor stores energy in the form of a magnetic field.
- Let's denote the charge on the capacitor as Q and the current through the inductor as I. The potential across the capacitor is given by:
VC=QC
- The back EMF (electromotive force) across the inductor is given by:
VL=−LdIdt
- Since the capacitor is discharging, we can express the current I as:
I=−dQdt
- Substituting this into the equation for the inductor gives:
VL=−Lddt(−dQdt)=Ld2Qdt2
- Since the capacitor and inductor are in parallel, their potentials are equal:
QC=Ld2Qdt2
- Rearranging gives us:
Ld2Qdt2+QC=0
- This resembles the equation of motion for simple harmonic motion (SHM), which is:
md2xdt2+kx=0
- In SHM, m is the mass and k is the spring constant. In our electrical analogy:
- The electrical analog of mass m is the inductor L.
- The electrical analog of the spring constant k is 1C.
- Therefore, the electrical analog of the spring constant k is:
k=1C
The electrical analog of a spring constant k is 1C.
Topper's Solved these Questions
- ALTERNATING CURRENT BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ALTERNATING CURRENT EXERCISE - Assignment (Section - B) (Objective Type Questions (One option is correct))
14 Videos
- ALTERNATING CURRENT BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ALTERNATING CURRENT EXERCISE - Assignment (Section - C ) (Objective Type Questions) ( More than one option are correct)
2 Videos
- ALTERNATING CURRENT BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ALTERNATING CURRENT EXERCISE - Try Yourself
15 Videos
- ATOMSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ATOMSEXERCISE - ASSIGNMENT SECTION J (Aakash Challengers )
5 Videos
Similar Questions
The frequency of oscillations of a mass m connected horizontally by a spring of spring constant k is 4 HZ. When the spring is replaced by two identical spring as shown in figure. Then the effective frequency is

View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View Solution
Knowledge Check
What is the mechanical equivalent of spring constant k in LC oscillating circuit?
A1LB1CCLCD1LC
One end of a light spring of spring constant k is fixed to a wall and the other end is tied to a block placed on a smooth horizontal surface. In a displacement, the work by the spring is 12kx2. The possible cases are
View SolutionThe frequency f of vibrations of a mass m suspended from a spring of spring constant k is given by f=Cmxky , where C is a dimensionnless constant. The values of xandy are, respectively,
View SolutionThe frequency f of vibrations of a mass m suspended from a spring of spring constant k is given by f=Cmxky , where C is a dimensionnless constant. The values of xandy are, respectively,
View SolutionThe frequency f of vibrations of a mass m suspended from a spring of spring constant k is given by f=Cmxky , where C is a dimensionnless constant. The values of xandy are, respectively,
View SolutionThere are two identical spring each of spring constant k. here springs, pulley and rods are massless and the block has mass m . What is the extension of each spring at equilibrium?
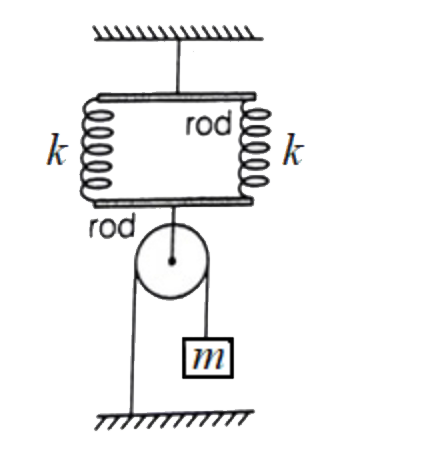
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View SolutionIn the figure all spring are identical having spring constant k and mass m each The block also mass m The frequency of oscillation of the block is
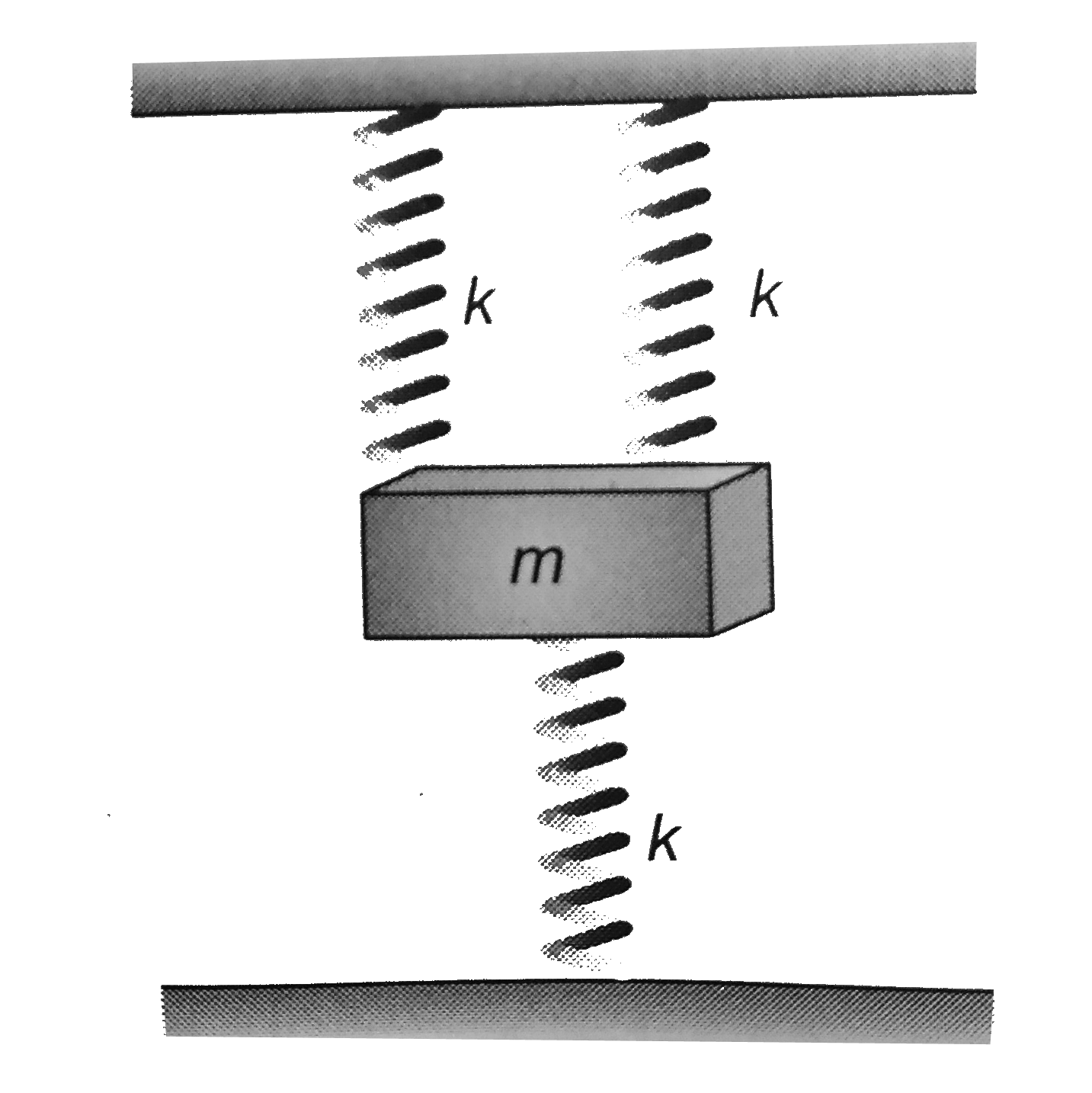
View Solution
