Assertion: In a string wave, during reflection from fix boundary, the reflected wave is inverted.
Reason: The force on string by clamp is in downward direction while string is pulling the clamp is upward direction.
If both assertion and reason are true and reason is the correct explanation of assertion.
If both assertion and reason are true but reason is not the correct explanation of assertion.
If assertion is true but reason is false.
If both assertion and reason are false.
The correct Answer is:A
To solve the question, we need to analyze both the assertion and the reason given.
1. Understanding the Assertion:
- The assertion states that "In a string wave, during reflection from a fixed boundary, the reflected wave is inverted."
- This is a well-known phenomenon in wave mechanics. When a wave traveling along a string reaches a fixed boundary, it reflects back and undergoes a phase change of 180 degrees (or π radians), which results in the wave being inverted.
2. Understanding the Reason:
- The reason provided is that "The force on the string by the clamp is in the downward direction while the string is pulling the clamp in the upward direction."
- This statement describes the forces acting on the string at the fixed boundary (the clamp). The clamp exerts a downward force on the string, while the tension in the string pulls upward on the clamp. This opposing action leads to the inversion of the wave upon reflection.
3. Linking the Assertion and Reason:
- The reason explains why the assertion is true. The downward force from the clamp creates a situation where the wave reflects with inversion. Thus, the inversion of the wave is a direct consequence of the forces acting at the fixed boundary.
4. Conclusion:
- Both the assertion and the reason are correct, and the reason provides a correct explanation for the assertion.
Final Answer:
- Both the assertion and the reason are true, and the reason is the correct explanation of the assertion.
- The assertion states that "In a string wave, during reflection from a fixed boundary, the reflected wave is inverted."
- This is a well-known phenomenon in wave mechanics. When a wave traveling along a string reaches a fixed boundary, it reflects back and undergoes a phase change of 180 degrees (or π radians), which results in the wave being inverted.
- The reason provided is that "The force on the string by the clamp is in the downward direction while the string is pulling the clamp in the upward direction."
- This statement describes the forces acting on the string at the fixed boundary (the clamp). The clamp exerts a downward force on the string, while the tension in the string pulls upward on the clamp. This opposing action leads to the inversion of the wave upon reflection.
- The reason explains why the assertion is true. The downward force from the clamp creates a situation where the wave reflects with inversion. Thus, the inversion of the wave is a direct consequence of the forces acting at the fixed boundary.
- Both the assertion and the reason are correct, and the reason provides a correct explanation for the assertion.
- Both the assertion and the reason are true, and the reason is the correct explanation of the assertion.
Similar Questions
A standing wave is produced on a string on a string clamped at one end and free at the other. The length of the string
View SolutionAssertion : A string wave traveling towards a free end changes its direction of motion but phase
Reason : When string wave reaches the free end there is no medium present in front of it.remains constant after reflection.
View SolutionA wave pulse, travelling on a two piece string, gets partically reflected and partically transmitted at the junction, The reflected wave is inverted in shape as compard to the incident one. If the incident wave has speed v and the transmitted wave v'
View SolutionAssertion:- Transvers waves are produced in a very long string fixed at one end. Near the free end only progressive wave is observed.
Reason:- Energy of reflected wave does does not reach the free end.
View SolutionExplain the formation of standing waves in a string clamped at both ends and discuss the various modes of vibration.
View Solution(A) : Sky wave is reflected by ionosphere
(R) : The reflected wave is out of phase of incident waveand reach the receiving antenna along with the direct wave from transmitting antenna causes in interference.
View SolutionOne end of ideal string tied up with fixed suppot & other end is tied with a bob. The string is released from horizontal position. When string makes an angle of θ with vertically downward direction then the acceleration vector of bob is horizontal then θ is
View SolutionConsider a wave sent down a string in the positive direction whose equation is given is
y=y0sin[ω(t−xv)]
The wave is propagated along because each string segment pulls upward and downward on the segment adjacent to it a slightly larger value of x and, as a result does work upon the string segment to which wave is travelling.
For example, the portion of string at point A is going upward, and will pull the portion at point B upward as well. In fact, at any point along the string, each segment of the string is pulling on the segment just adjacent and to its right, causing the wagve to propagate. It is by this process that the energy is sent along the string.
Now we try to calculate how much energy is propagated down the stirng per second
Ty=tsinθ≈Ttanθ⇒Ty=−T∂y∂x
(The negative sign appears because as shown in the figure II, the slope is negative) the force will act through a distance
dy=vydt=∂y∂tdt
Therefore work done by force in time dt is
dW=Tydy=−T(∂y∂x)(∂y∂t)dt⇒dW=ω2y20Tvcos2[ω(t−xV)]dt.....(A)
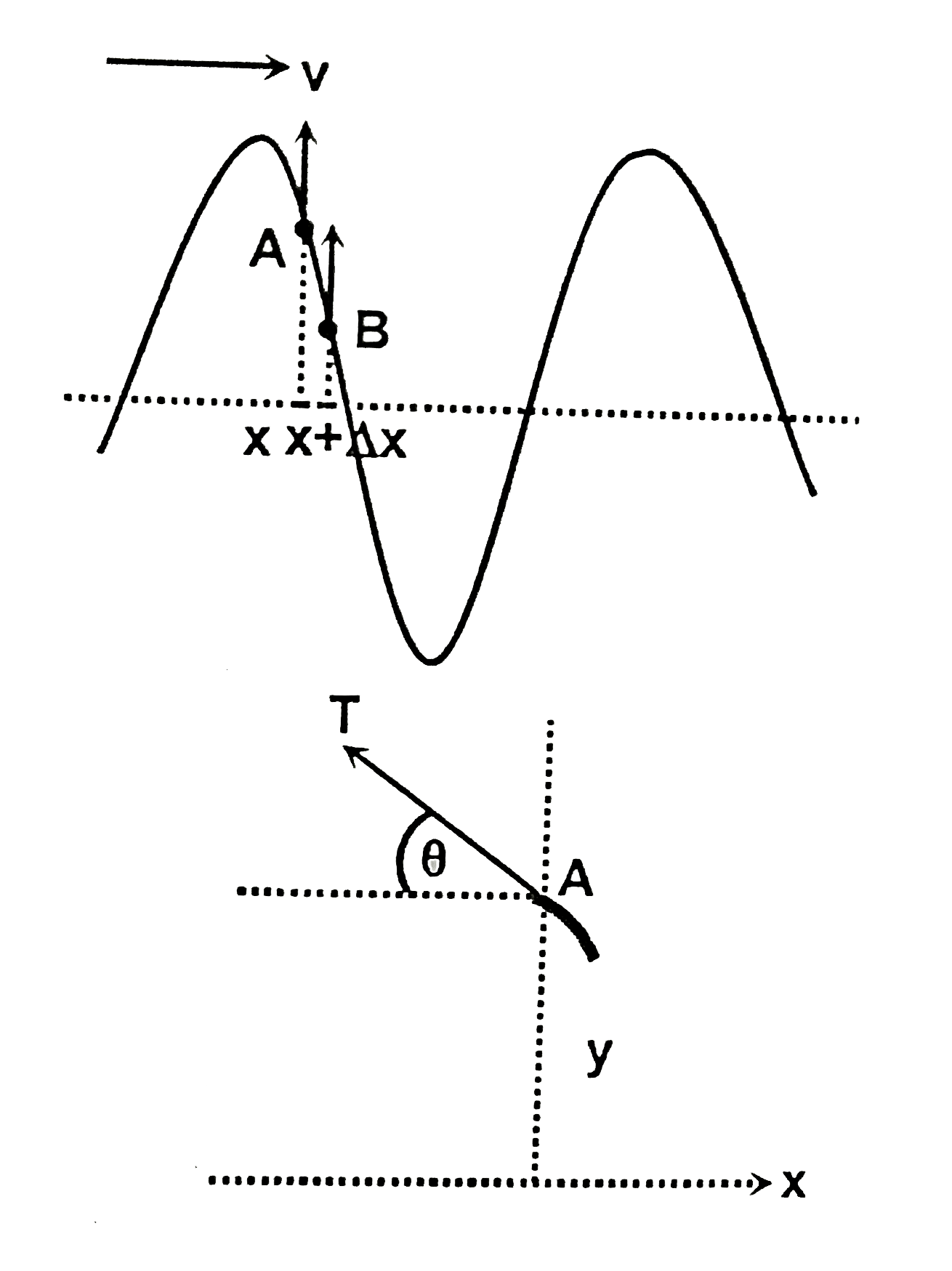
The average power transmitted down the string (i.e. the average energy transfer or sent down it per second) is
View SolutionConsider a standing wave formed on a string . It results due to the superposition of two waves travelling in opposite directions . The waves are travelling along the length of the string in the x - direction and displacements of elements on the string are along the y - direction . Individual equations of the two waves can be expressed as
Y1=6(cm)sin[5(rad/cm)x−4(rad/s)t]
Y2=6(cm)sin[5(rad/cm)x+4(rad/s)t] Here x and y are in cm.
Answer the following questions.
If one end of the string is at x=0 , positions of the nodes can be described as
View SolutionConsider a standing wave formed on a string . It results due to the superposition of two waves travelling in opposite directions . The waves are travelling along the length of the string in the x - direction and displacements of elements on the string are along the y - direction . Individual equations of the two waves can be expressed as
Y1=6(cm)sin[5(rad/cm)x−4(rad/s)t]
Y2=6(cm)sin[5(rad/cm)x+4(rad/s)t] Here x and y are in cm.
Answer the following questions.
Amplitude of simple harmonic motion of a point on the string that is located at x=1.8cm will be
View Solution
