Hailstorms are observed to strike the surface of a frozen lake at an angle of 30∘ with the vertical and rebound at an angle of 60∘ with vertical. Assuming the contact to be smooth, the coefficient of restitution is
e=1√3
e=13
e=√3
e = 3
The correct Answer is:B
To find the coefficient of restitution (e) for the hailstones striking and rebounding from the frozen lake, we can follow these steps:
Step 1: Understanding the Angles
The hailstones strike the surface at an angle of 30∘ with the vertical and rebound at an angle of 60∘ with the vertical.
Step 2: Identify Components of Velocity
Let U be the initial velocity of the hailstone before impact, and V be the velocity after the impact. We can break these velocities into components:
- For the initial velocity U:
- Vertical component (perpendicular to the surface): Ucos(30∘)
- Horizontal component (parallel to the surface): Usin(30∘)
- For the final velocity V:
- Vertical component (perpendicular to the surface): Vcos(60∘)
- Horizontal component (parallel to the surface): Vsin(60∘)
Step 3: Equating Horizontal Components
Since there is no change in the horizontal component of velocity (the surface is smooth), we can set the horizontal components equal:
Usin(30∘)=Vsin(60∘)
Substituting the values of sine:
U⋅12=V⋅√32
This simplifies to:
U=√3V
Step 4: Applying the Coefficient of Restitution Formula
The coefficient of restitution e is defined as the ratio of the relative velocity after impact to the relative velocity before impact in the direction perpendicular to the surface:
e=Relative velocity after impactRelative velocity before impact
In this case:
- The relative velocity before impact (downward) is Ucos(30∘)
- The relative velocity after impact (upward) is Vcos(60∘)
Substituting the values:
e=0−Vcos(60∘)Ucos(30∘)
Since the ground is stationary, the velocity of the ground is 0.
Step 5: Substitute the Values
Substituting the cosine values:
e=−V⋅12U⋅√32
This simplifies to:
e=−V/2U⋅√3/2=−VU√3
Step 6: Substitute U from Step 3
From Step 3, we know U=√3V:
e=−V√3V⋅√3=−V3V=−13
Since we are interested in the magnitude:
e=13
Final Answer
The coefficient of restitution is:
13
The hailstones strike the surface at an angle of 30∘ with the vertical and rebound at an angle of 60∘ with the vertical.
Let U be the initial velocity of the hailstone before impact, and V be the velocity after the impact. We can break these velocities into components:
- Vertical component (perpendicular to the surface): Ucos(30∘)
- Horizontal component (parallel to the surface): Usin(30∘)
- Vertical component (perpendicular to the surface): Vcos(60∘)
- Horizontal component (parallel to the surface): Vsin(60∘)
Since there is no change in the horizontal component of velocity (the surface is smooth), we can set the horizontal components equal:
Usin(30∘)=Vsin(60∘)
Substituting the values of sine:
U⋅12=V⋅√32
This simplifies to:
U=√3V
The coefficient of restitution e is defined as the ratio of the relative velocity after impact to the relative velocity before impact in the direction perpendicular to the surface:
e=Relative velocity after impactRelative velocity before impact
In this case:
- The relative velocity before impact (downward) is Ucos(30∘)
- The relative velocity after impact (upward) is Vcos(60∘)
e=0−Vcos(60∘)Ucos(30∘)
Since the ground is stationary, the velocity of the ground is 0.
Substituting the cosine values:
e=−V⋅12U⋅√32
This simplifies to:
e=−V/2U⋅√3/2=−VU√3
From Step 3, we know U=√3V:
e=−V√3V⋅√3=−V3V=−13
Since we are interested in the magnitude:
e=13
The coefficient of restitution is:
13
Similar Questions
A plane wavefront incident on a reflecting surface at and angle of 30∘ with vertical. Find the angle (acute) of reflected wave with vertical.
View SolutionA force of 4N is inclined at an angle of 60∘ from the vertical. Find out its components along horizontal and vertical directions.

View SolutionA force of 4N is inclined at an angle of 60∘ from the vertical. Find out its components along horizontal and vertical directions.

View SolutionDuring a rainstorm the raindrops are observed to strike the ground at an angle of 37∘ with the vertical. The wind speed is 4.5 m/s. Assuming that the horizontal velocity component of the raindrops is same as the speed of air, what is the vertical component of raindrops? What is their speed ?
View SolutionA particle strikes a smooth horizontal surface at an angle θ>0 and it rebounds at an angle ϕ as shown

View SolutionA ball strikes a smooth horizontal ground at an angle of 45∘ with the vertical. What cannot be the possible angle of its velocity with the vertical after the collision. (Assume e ≤ 1).
View Solution[Find by vector method the horizontal force and the force inclined at an angle of 60∘ to the vertical whose resultant is a vertical force P.]
View SolutionIn the figure shown, a particle P strikes the inclined smooth plane horizontally and rebounds vertically. If the angle θ is 60∘ then the coefficient of restitution is:

View SolutionA particle of mass m moving with a speed u strikes a smooth horizontal surface at an angle 45∘. The particle rebounds at an angle ϕ with speed v. If coefficient of restituion is 1√3, then angle ϕ is
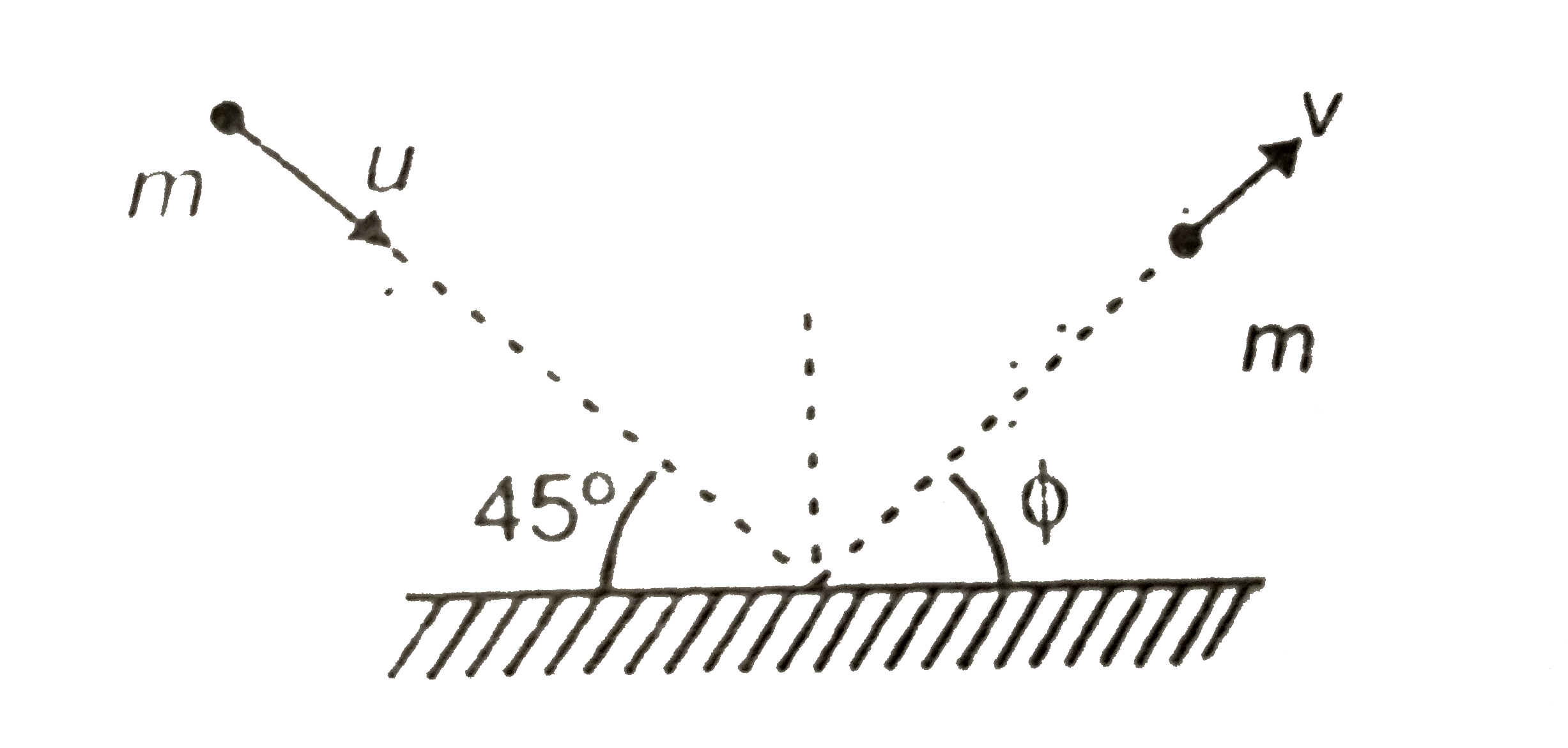
View SolutionA particle of mass m moving with a speed u strikes a smooth horizontal surface at an angle 45∘. The particle rebounds at an angle ϕ with speed v. If coefficient of restituion is 1√3, then angle ϕ is

View Solution
