A ball strikes a smooth horizontal ground at an angle of 45∘ with the vertical. What cannot be the possible angle of its velocity with the vertical after the collision. (Assume e ≤ 1).
45∘
30∘
53∘
60∘
The correct Answer is:B
To solve the problem, we need to analyze the motion of a ball that strikes a smooth horizontal ground at an angle of 45 degrees with the vertical. We will determine the possible angles of its velocity with the vertical after the collision, given that the coefficient of restitution e is less than or equal to 1.
1. Identify Initial Conditions:
- The ball strikes the ground at an angle of 45∘ with the vertical.
- This means the angle with the horizontal is 90∘−45∘=45∘.
2. Resolve Initial Velocity Components:
- Let the initial velocity of the ball be V.
- The vertical component of the velocity before the collision is:
Vvertical=Vcos(45∘)=V√2
- The horizontal component of the velocity before the collision is:
Vhorizontal=Vsin(45∘)=V√2
3. Understand the Collision:
- The ground is smooth, meaning there is no friction. Therefore, the horizontal component of the velocity remains unchanged after the collision.
- The vertical component of the velocity after the collision will be affected by the coefficient of restitution e:
Uvertical=e⋅Vvertical=e⋅V√2
4. Determine the New Velocity Components:
- After the collision, the horizontal component remains:
Uhorizontal=V√2
- The new vertical component is:
Uvertical=e⋅V√2
5. Calculate the Angle After Collision:
- The angle α that the velocity makes with the vertical after the collision can be determined using the tangent function:
tan(α)=UhorizontalUvertical=V√2e⋅V√2=1e
6. Analyze the Coefficient of Restitution:
- Since e≤1, it follows that 1e≥1.
- Therefore, tan(α)≥1, which implies:
α≥45∘
7. Evaluate the Given Options:
- The possible angles given are 45∘,30∘,53∘, and 16∘.
- Since α must be greater than or equal to 45∘, the angle 30∘ cannot be achieved.
Conclusion:
The angle that cannot be the possible angle of the ball's velocity with the vertical after the collision is 30 degrees.
- The ball strikes the ground at an angle of 45∘ with the vertical.
- This means the angle with the horizontal is 90∘−45∘=45∘.
- Let the initial velocity of the ball be V.
- The vertical component of the velocity before the collision is:
Vvertical=Vcos(45∘)=V√2
- The horizontal component of the velocity before the collision is:
Vhorizontal=Vsin(45∘)=V√2
- The ground is smooth, meaning there is no friction. Therefore, the horizontal component of the velocity remains unchanged after the collision.
- The vertical component of the velocity after the collision will be affected by the coefficient of restitution e:
Uvertical=e⋅Vvertical=e⋅V√2
- After the collision, the horizontal component remains:
Uhorizontal=V√2
- The new vertical component is:
Uvertical=e⋅V√2
- The angle α that the velocity makes with the vertical after the collision can be determined using the tangent function:
tan(α)=UhorizontalUvertical=V√2e⋅V√2=1e
- Since e≤1, it follows that 1e≥1.
- Therefore, tan(α)≥1, which implies:
α≥45∘
- The possible angles given are 45∘,30∘,53∘, and 16∘.
- Since α must be greater than or equal to 45∘, the angle 30∘ cannot be achieved.
The angle that cannot be the possible angle of the ball's velocity with the vertical after the collision is 30 degrees.
Similar Questions
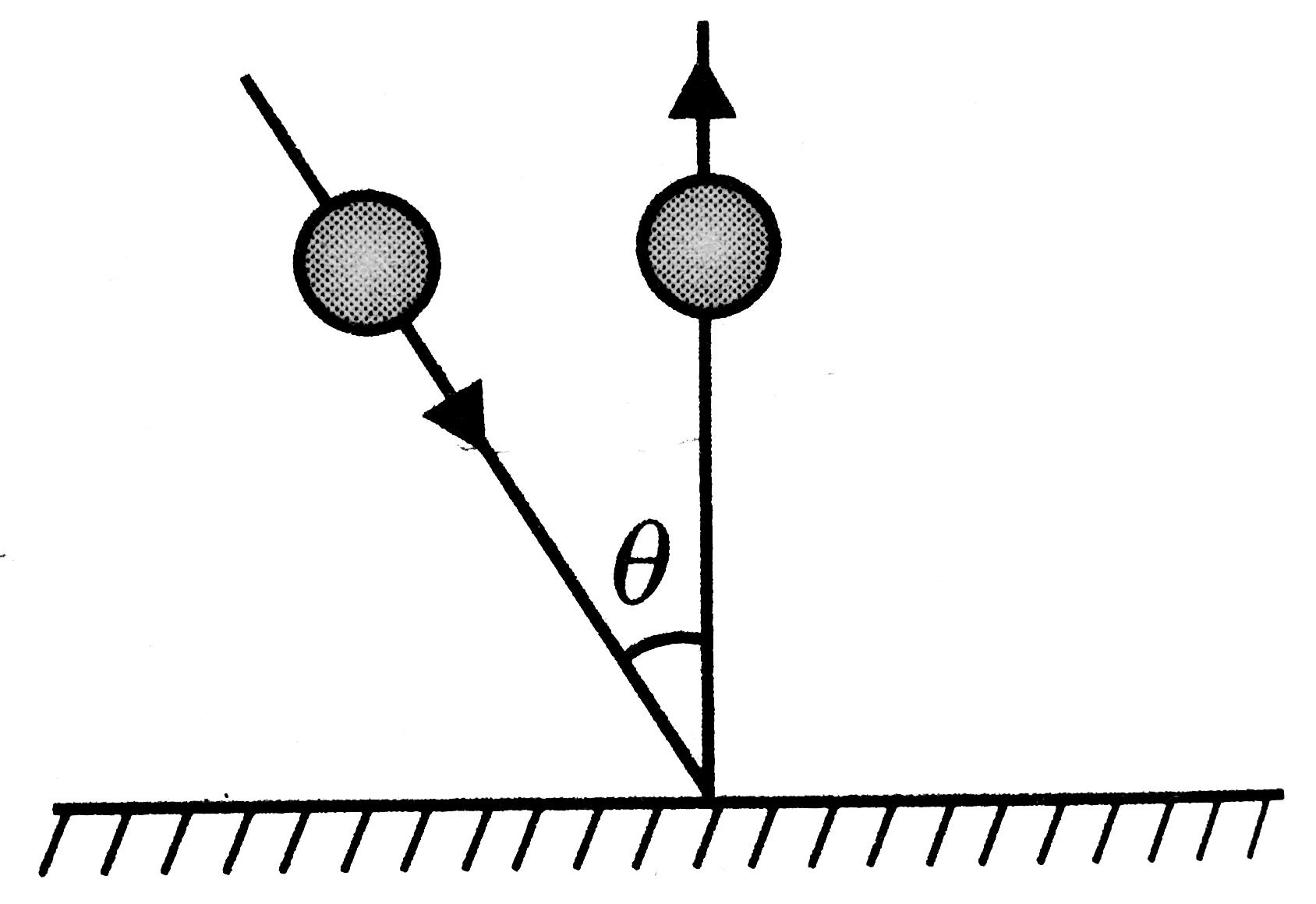
A ball of mass 1kg moving with a velocity of 5m/s collides elastically with rough ground at an angle θ with the vertical as shown in Fig. What can be the minimum coefficient of friction if ball rebounds vertically after collision? (given tanθ=2)
View SolutionA particle strikes a smooth horizontal surface at an angle of 45∘ with a velocity of 100m/s and rebounds. If the coefficient of restitution between the floor and the particle is 0.57 then the angle which the velocity of the particle after it rebounds will make with the floor is
View SolutionA football is kicked at an angle of 30∘ with the vertical, so if the horizontal component of its velocity is 20ms−1, determine its maximum height.
View SolutionA particle is projected from a point A with velocity √2u an angle of 45∘ with horizontal as shown in figure. It strikes the plane BC at right angles. The velocity of the particle at the time of collision is

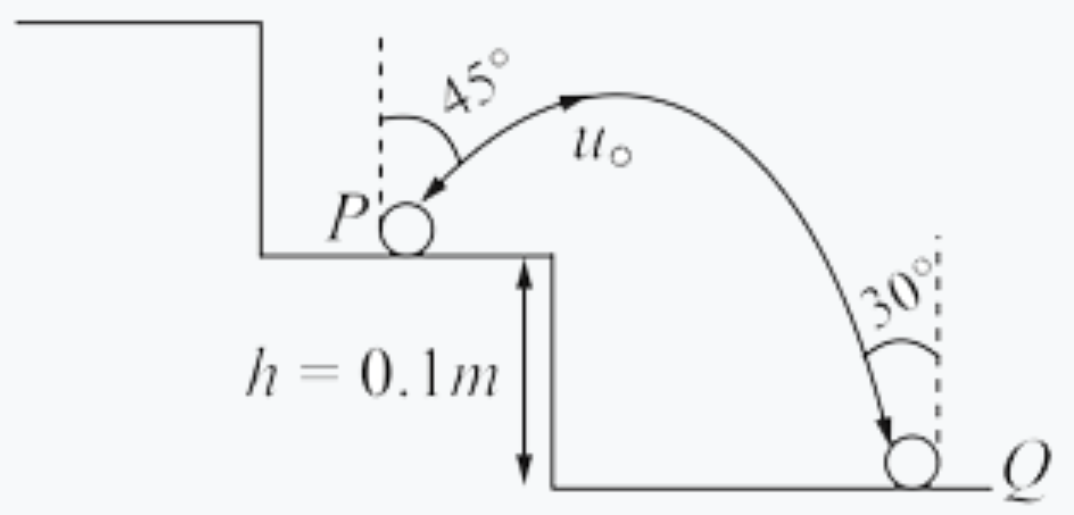
View SolutionA ball is dropped onto a step at a point P and rebounds with velocity u∘ at an angle of 45∘with the vertical. The value of u0 knowing that just before the ball hits the point Q its velocity forms an angle 30∘ with the vertical is: (g=10m/s2)
View SolutionHailstorms are observed to strike the surface of a frozen lake at an angle of 30∘ with the vertical and rebound at an angle of 60∘ with vertical. Assuming the contact to be smooth, the coefficient of restitution is
View SolutionA steel ball strikes a fixed smooth steel plate placed on a horizontal surface at an angle θ with the vertical. If the coefficient of restitution is e, the angle at which the rebound will take place is:
View SolutionA steel ball strikes a fixed smooth steel plate placed on a horizontal surface atan angle θ with the vertical. If the coefficient of restitution is e, the angle at which the rebound will take place is:
View SolutionDuring a rainstorm the raindrops are observed to strike the ground at an angle of 37∘ with the vertical. The wind speed is 4.5 m/s. Assuming that the horizontal velocity component of the raindrops is same as the speed of air, what is the vertical component of raindrops? What is their speed ?
View SolutionA glass ball collides with a smooth horizontal surface (xz plane) with a velocity V=ai−bj. If the coefficient of restitution of collision be e, the velocity of the ball just after the collision will be
View Solution